
1、能够把研究直线与圆锥曲线位置关系的问题转化为研究方程组的解的问题;
2、会利用直线与圆锥曲线方程所组成的方程组消去一个变量,将交点问题(包括公共点个数、与交点坐标有关的问题)转化为一元二次方程根的问题,结合根与系数关系及判别式解决问题;
3、能够运用数形结合,迅速判断某些直线和圆锥曲线的位置关系.
知识概要
1、交点问题;
2、弦的中点问题.
基础练习
1、直线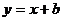 与抛物线
与抛物线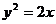 ,当
,当 _________时,有且只有一个公共点;当
_________时,有且只有一个公共点;当 _________时,有两个不同的公共点;当
_________时,有两个不同的公共点;当 _________时,无公共点.
_________时,无公共点.
2、若直线 和椭圆
和椭圆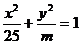 恒有公共点,则实数
恒有公共点,则实数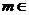 ___________.
___________.
3、已知双曲线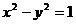 和斜率为
和斜率为 的直线
的直线 交于A、B两点,当
交于A、B两点,当 变化时,线段AB的中点M的坐标
变化时,线段AB的中点M的坐标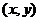 满足的方程是______________.
满足的方程是______________.
4、直线 与双曲线
与双曲线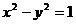 有且只有一个公共点,则
有且只有一个公共点,则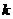 的取值是_____________.
的取值是_____________.
5、椭圆 中过点P(1,1)的弦恰好被P点平分,则此弦所在的直线方程是_________________.
中过点P(1,1)的弦恰好被P点平分,则此弦所在的直线方程是_________________.
例题讲解
例1、已知双曲线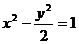 与点P(1,2),过P点作直线
与点P(1,2),过P点作直线 与双曲线交于A、B两点,若P为AB的中点.
与双曲线交于A、B两点,若P为AB的中点.
(1)求直线AB的方程;
(2)若Q(1,1),证明不存在以Q为中点的弦.
例2、直线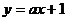 与双曲线
与双曲线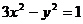 交于A、B两点.
交于A、B两点.
(1)当 为何值时,A、B分别在双曲线的两支上?
为何值时,A、B分别在双曲线的两支上?
(2)当 为何值时,以AB为直径的圆过坐标原点?
为何值时,以AB为直径的圆过坐标原点?
例3、斜率为1的直线与椭圆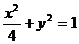 相交于M、N两点,求线段M、N的垂直平分线在
相交于M、N两点,求线段M、N的垂直平分线在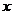 轴上的截距的取值范围.
轴上的截距的取值范围.
例4、过点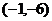 的直线
的直线 与抛物线
与抛物线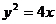 交于A、B两点,若
交于A、B两点,若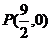 ,
,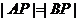 求直线
求直线 的斜率.
的斜率.
课后作业
班级_______学号__________姓名_________
1、过点(2,4)作直线与抛物线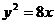 只有一个公共点,这样的直线有( )
只有一个公共点,这样的直线有( )
A.一条 B.两条 C.三条 D.四条
2、设椭圆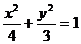 的长轴两端点为M、N,异于M、N的点P在椭圆上,则PM与PN的斜率之积为( )
的长轴两端点为M、N,异于M、N的点P在椭圆上,则PM与PN的斜率之积为( )
A.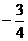 B.
B. C.
C.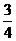 D.
D.
3、双曲线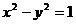 的左焦点为F,点P为左支下半支上任意一点(异于顶点),则直线PF的斜率的变化范围是( )
的左焦点为F,点P为左支下半支上任意一点(异于顶点),则直线PF的斜率的变化范围是( )
A.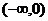 B.
B. C.
C.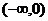 ∪
∪ D.
D.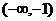 ∪
∪
4、已知抛物线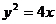 关于直线
关于直线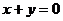 对称的抛物线方程是___________.
对称的抛物线方程是___________.
5、直线 与椭圆
与椭圆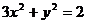 交于A、B两点,求以AB为直径的圆的方程.
交于A、B两点,求以AB为直径的圆的方程.
6、已知直线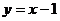 和椭圆
和椭圆 交于A、B两点,若以AB为直径的圆过椭圆的左焦点F,求
交于A、B两点,若以AB为直径的圆过椭圆的左焦点F,求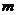 的值.
的值.
7、过点A(1,0)的直线 与中心在原点,焦点在
与中心在原点,焦点在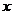 轴上,且离心率为
轴上,且离心率为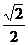 的椭圆C相交于B、C两点,直线
的椭圆C相交于B、C两点,直线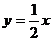 过线段BC的中点,同时椭圆C上存在一点与右焦点关于直线
过线段BC的中点,同时椭圆C上存在一点与右焦点关于直线 对称,试求直线
对称,试求直线 与椭圆C的方程.
与椭圆C的方程.
8、一个正三角形的三个顶点都在双曲线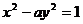 的右支上,其中一个顶点是双曲线的右顶点,求实数
的右支上,其中一个顶点是双曲线的右顶点,求实数 的取值范围.
的取值范围.
高三数学教学案 第八章 圆锥曲线
第七课时 直线与圆锥曲线的位置关系(二)
考纲摘录
能正确熟练地计算直线和圆锥曲线相交所得线段的长.
知识概要
1、弦长公式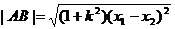 ,但计算焦点弦长时可运用定义“曲线上的点到焦点的距离与到相应准线的距离之比等于离心率
,但计算焦点弦长时可运用定义“曲线上的点到焦点的距离与到相应准线的距离之比等于离心率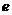 ”以简化弦长计算;
”以简化弦长计算;
2、椭圆的焦半径公式.
基础练习
1、斜率为1的直线经过抛物线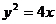 的焦点与抛物线相交于两点A、B,则|AB|=______________.
的焦点与抛物线相交于两点A、B,则|AB|=______________.
2、过双曲线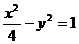 的左焦点F的直线交双曲线于
的左焦点F的直线交双曲线于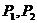 两点,若
两点,若 ,则这样的直线一共有( )
,则这样的直线一共有( )
A.1条 B.2条 C.3条 D.4条
3、直线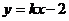 交抛物线
交抛物线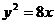 于A、B两点,若AB中点的横坐标为2,则|AB|为( )
于A、B两点,若AB中点的横坐标为2,则|AB|为( )
A.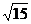 B.
B. C.
C. D.
D.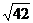
4、椭圆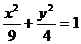 的焦点为
的焦点为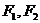 ,点P为其上动点,当
,点P为其上动点,当 为钝角时,点P横坐标的取值范围是______________.
为钝角时,点P横坐标的取值范围是______________.
5、两条渐近线为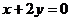 ,
, ,且截直线
,且截直线 所得弦长为
所得弦长为 的双曲线方程为( )
的双曲线方程为( )
A.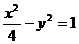 B.
B.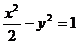 C.
C.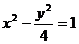 D.
D.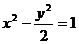
例题讲解
例1、直线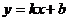 交抛物线
交抛物线 于A、B两点,已知
于A、B两点,已知 ,线段AB中点纵坐标为
,线段AB中点纵坐标为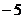 ,求
,求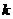 ,
,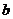 的值.
的值.
例2、过椭圆C: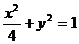 右焦点作一直线
右焦点作一直线 交椭圆C于M、N两点,且M、N到直线
交椭圆C于M、N两点,且M、N到直线 的距离之和为
的距离之和为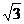 ,求直线
,求直线 的方程.
的方程.
例3、椭圆 与直线
与直线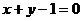 相交于A、B两点,C是AB的中点,若|AB|=
相交于A、B两点,C是AB的中点,若|AB|=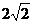 ,OC的斜率为
,OC的斜率为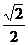 ,求椭圆的方程.
,求椭圆的方程.
例4、已知双曲线 的左焦点为
的左焦点为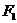 ,过
,过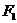 分别作垂直于
分别作垂直于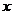 轴的直线及斜率为
轴的直线及斜率为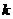 的直线,它们与双曲线分别相交于A、B及C、D,问:是否存在这样的
的直线,它们与双曲线分别相交于A、B及C、D,问:是否存在这样的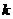 ,使|AB|=|CD|?如果存在,求出
,使|AB|=|CD|?如果存在,求出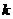 ,如果不存在,说明理由.
,如果不存在,说明理由.
课后作业
班级_______学号__________姓名_________
1、已知椭圆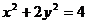 ,则以(1,1)为中点的弦的长度为____________.
,则以(1,1)为中点的弦的长度为____________.
2、若双曲线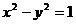 的右支上一点
的右支上一点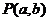 到直线
到直线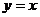 的距离为
的距离为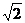 ,则
,则 的值为____________.
的值为____________.
3、抛物线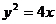 的焦点F作倾斜角为
的焦点F作倾斜角为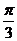 的弦AB,则|AB|等于___________.
的弦AB,则|AB|等于___________.
4、若双曲线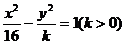 的一条准线恰为圆
的一条准线恰为圆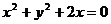 的一条切线,则
的一条切线,则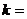 ___________.
___________.
5、已知点A(0,1)是椭圆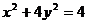 上的一点,P是椭圆上的动点,当弦AP长度最大时,点P的坐标是__________.
上的一点,P是椭圆上的动点,当弦AP长度最大时,点P的坐标是__________.
6、已知双曲线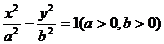 的离心率
的离心率 ,过点
,过点 和点
和点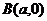 的直线与原点的距离是
的直线与原点的距离是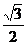 ,
,
(1)求双曲线的方程;
(2)求过双曲线的左焦点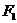 ,倾斜角为
,倾斜角为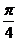 的直线被双曲线所截得的弦长.
的直线被双曲线所截得的弦长.
7、如图,过抛物线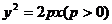 上一定点
上一定点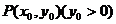 ,作两条直线分别交抛物线于
,作两条直线分别交抛物线于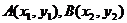
(1)求该抛物线上纵坐标为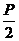 的点到其焦点F的距离;
的点到其焦点F的距离;
(2)当PA与PB的斜率存在且倾斜角互补时,求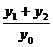 的值,并证明直线AB的斜率是非零常数.
的值,并证明直线AB的斜率是非零常数.
8、斜率为1的直线过椭圆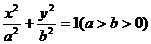 的左焦点
的左焦点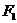 ,且与椭圆相交于A、B两点,求证:|AB|小于椭圆的短轴长.
,且与椭圆相交于A、B两点,求证:|AB|小于椭圆的短轴长.
高三数学教学案 第八章 圆锥曲线
第八课时 直线与圆锥曲线的位置关系(三)
考纲摘录
能够解决直线与圆锥曲线的比较复杂的综合问题.
基础练习
1、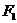 ,
,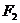 是椭圆
是椭圆 的两个焦点,过
的两个焦点,过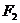 作倾斜角为
作倾斜角为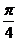 的弦AB,则
的弦AB,则 的面积为( )
的面积为( )
A. B.
B.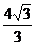 C.
C. D.
D.
2、已知AB是双曲线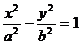 中过右焦点F的弦,且A、B均在双曲线的右支上,则以AB为直径的圆与右准线
中过右焦点F的弦,且A、B均在双曲线的右支上,则以AB为直径的圆与右准线 的位置关系是( )
的位置关系是( )
A.相切 B.相离 C.相交 D.不确定
3、已知抛物线 上三点A、B、C且A(-1,1),AB⊥BC,当点B移动时,点C的横坐标的取值范围是( )
上三点A、B、C且A(-1,1),AB⊥BC,当点B移动时,点C的横坐标的取值范围是( )
A.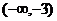 B.[-3,1] C.[1,+
B.[-3,1] C.[1,+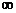 ) D.
) D.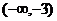 ∪
∪ 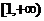
4、M是椭圆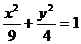 上任一点,
上任一点,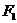 ,
,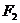 为两焦点,I是
为两焦点,I是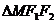 的内心,延长MI交
的内心,延长MI交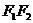 于N,则
于N,则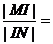 ______________.
______________.
例题讲解
例1、在椭圆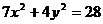 上求一点,使它到直线
上求一点,使它到直线 :
: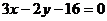 的距离最短,并求此距离.
的距离最短,并求此距离.
例2、椭圆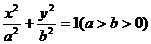 与直线
与直线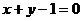 相交于P、Q两点,且OP⊥OQ(O为原点)
相交于P、Q两点,且OP⊥OQ(O为原点)
(1)求证: 等于定值;
等于定值;
(2)若椭圆离心率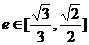 时,求椭圆长轴的取值范围.
时,求椭圆长轴的取值范围.
例3、已知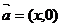 ,
,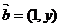 且
且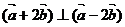
(1)求点 的轨迹C的方程;
的轨迹C的方程;
(2)若点M在曲线C上,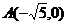 ,
,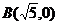 且
且 =3,求
=3,求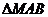 的面积;
的面积;
(3)曲线C 上是否存在一点N,使它到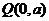 的最近距离是3?如果存在,求出点N的坐标;否则,请说明理由.
的最近距离是3?如果存在,求出点N的坐标;否则,请说明理由.
例4、给定抛物线C: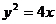 ,F是C的焦点,过点F的直线
,F是C的焦点,过点F的直线 与C相交于A、B两点,
与C相交于A、B两点,
(1)设 的斜率是1,求
的斜率是1,求 与
与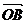 夹角的大小;
夹角的大小;
(2)设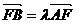 ,若
,若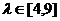 ,求
,求 在
在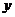 轴上截距的变化范围.
轴上截距的变化范围.
课后作业
班级_______学号__________姓名_________
1、抛物线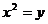 关于直线
关于直线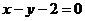 对称的抛物线的焦点坐标是( )
对称的抛物线的焦点坐标是( )
A. B.
B. C.
C.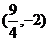 D.
D.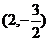
2、直线 与曲线
与曲线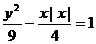 ( )
( )
A.没有交点 B.只有一个交点 C.有两个交点 D.有三个交点
3、方程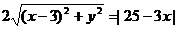 表示的曲线为( )
表示的曲线为( )
A.椭圆 B.双曲线 C.抛物线 D.圆
4、已知抛物线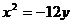 的切线
的切线 垂直于直线
垂直于直线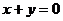 ,则直线
,则直线 的方程是____________.
的方程是____________.
5、经过抛物线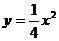 的焦点作直线交抛物线于
的焦点作直线交抛物线于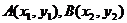 两点,若
两点,若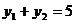 ,则线段AB的长等于__________.
,则线段AB的长等于__________.
6、双曲线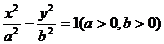 的焦距为2C,直线
的焦距为2C,直线 过点
过点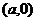 和
和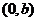 且点(1,0)到直线
且点(1,0)到直线 的距离与点
的距离与点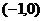 到直线
到直线 的距离之和
的距离之和 ,求双曲线的离心率
,求双曲线的离心率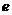 的取值范围.
的取值范围.
7、直线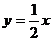 与抛物线
与抛物线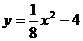 交于A、B两点,线段AB的垂直平分线与直线
交于A、B两点,线段AB的垂直平分线与直线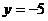 交于Q点,
交于Q点,
(1)求点Q的坐标;
(2)当P为抛物线上位于线段AB下方(含A,B)的动点时,求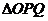 面积的最大值.
面积的最大值.
8、已知椭圆C的一个顶点为A(0,-1),焦点在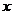 轴上,且其右焦点到直线的
轴上,且其右焦点到直线的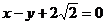 距离为3
距离为3
(1)求椭圆C的方程;
(2)试问能否找到一条斜率为 的直线
的直线 ,使与椭圆交于两个不同点M,N且使|AM|=|AN|,并指出
,使与椭圆交于两个不同点M,N且使|AM|=|AN|,并指出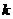 的取值范围.
的取值范围.
高三数学教学案 第八章 圆锥曲线
第九课时 求轨迹方程(一)
考纲摘录
理解轨迹的概念,能根据所给条件选择适当的直角坐标系,求轨迹的方程.
知识概要
1、轨迹与轨迹方程的区别与联系;
2、求轨迹方程的基本步骤--“四步一回头”.(见友P92)
基础练习
1、方程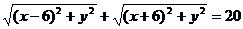 化简的结果是( )
化简的结果是( )
A.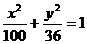 B.
B.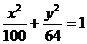 C.
C.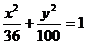 D.
D.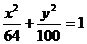
2、弦经过抛物线 的焦点,则该弦的中点的轨迹是( )
的焦点,则该弦的中点的轨迹是( )
A.抛物线 B.椭圆 C.双曲线 D.直线
3、点M与点F(4,0)的距离比它到直线 :
: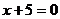 的距离小1,则点M的轨迹方程是_________________.
的距离小1,则点M的轨迹方程是_________________.
4、若动圆M与两个定圆⊙ :
: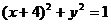 ,⊙
,⊙ :
: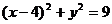 均外切,则动圆M的圆心M的轨迹方程是______________.
均外切,则动圆M的圆心M的轨迹方程是______________.
5、动圆与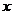 轴相切,且与直线
轴相切,且与直线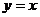 相交所得的弦长等于2,则动圆圆心的轨迹方程是______________.
相交所得的弦长等于2,则动圆圆心的轨迹方程是______________.
例题讲解
例1、已知△ABC中,|BC|=2, ,试求点A的轨迹方程,并说明轨迹是什么图形.
,试求点A的轨迹方程,并说明轨迹是什么图形.
例2、已知动点P到定点F(1,0)和直线 的距离之和等于4,求点P的轨迹方程.
的距离之和等于4,求点P的轨迹方程.
例3、抛物线C: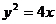 ,若椭圆的左焦点及相应准线与抛物线C的焦点F和准线分别重合(如图),求以椭圆短轴端点B与焦点F为两端点的线段中点P的轨迹方程.
,若椭圆的左焦点及相应准线与抛物线C的焦点F和准线分别重合(如图),求以椭圆短轴端点B与焦点F为两端点的线段中点P的轨迹方程.
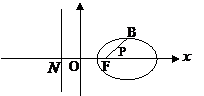
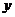
例4、已知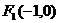 ,
, ,
, ,动点P满足
,动点P满足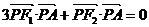 .
.
(1)求动点P的轨迹方程;
(2)是否存在点P,使得PA成为 的平分线?若存在,求出P点坐标,若不存在,说明理由.
的平分线?若存在,求出P点坐标,若不存在,说明理由.
课后作业
班级_______学号__________姓名_________
1、已知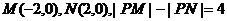 ,则动点P的轨迹是____________.
,则动点P的轨迹是____________.
2、已知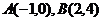 ,△ABC的面积为10,则动点C的轨迹方程是____________.
,△ABC的面积为10,则动点C的轨迹方程是____________.
3、一动圆M与⊙ :
: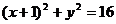 内切,且与⊙
内切,且与⊙ :
: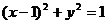 外切,则动圆圆心M的轨迹方程是___________.
外切,则动圆圆心M的轨迹方程是___________.
4、高10米和高15米的两根旗杆竖在地面上,且相距20米,则地面上到两旗杆的仰角相等的点P的轨迹是( )
A.圆 B.椭圆 C.双曲线 D.抛物线
5、动点P与两个定点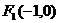 ,
, 连线的斜率之积等于
连线的斜率之积等于 ,求点P的轨迹方程,并就
,求点P的轨迹方程,并就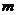 的不同取值讨论其轨迹的形状.
的不同取值讨论其轨迹的形状.
6、圆的方程为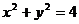 ,A,B两点的坐标分别为
,A,B两点的坐标分别为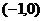 ,
,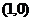 ,一抛物线经过A、B两点,而且以该圆的切线为准线,求抛物线的焦点的轨迹方程.
,一抛物线经过A、B两点,而且以该圆的切线为准线,求抛物线的焦点的轨迹方程.
7、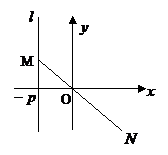 设点O是直角坐标系的原点,点M在直线
设点O是直角坐标系的原点,点M在直线 :
: 上移动,动点N在线段MO的延长线上,且满足
上移动,动点N在线段MO的延长线上,且满足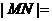
 .
.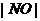 .
.
(1)求动点N的轨迹方程;
(2)当 时,求|MN|的最小值.
时,求|MN|的最小值.
高三数学教学案 第八章 圆锥曲线
第十课时 求轨迹方程(二)
考纲摘录
使学生进一步理解轨迹的概念,会使用除直接法和定义法外的其他方法求轨迹及轨迹
方程.
知识概要
相关点法,参数法,交轨法.
基础练习
1、点P是圆 上的动点,O是坐标原点,则线段OP的中点Q的轨迹方程是________________.
上的动点,O是坐标原点,则线段OP的中点Q的轨迹方程是________________.
2、过抛物线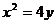 的焦点F作直线
的焦点F作直线 交抛物线于A、B两点,则弦AB的中点M的轨迹方程是______________.
交抛物线于A、B两点,则弦AB的中点M的轨迹方程是______________.
3、分别过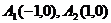 作两条互相垂直的直线,则它们的交点M的轨迹方程是_________________.
作两条互相垂直的直线,则它们的交点M的轨迹方程是_________________.
4、抛物线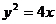 关于直线
关于直线 :
: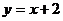 对称的曲线方程是______________.
对称的曲线方程是______________.
例题讲解
例1、过点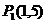 任作一直线
任作一直线 交
交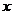 轴于点A,过点
轴于点A,过点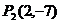 作
作 的垂线
的垂线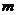 交
交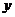 轴于点B,点M分有向线段
轴于点B,点M分有向线段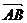 所成的比AM:MB=2:1,求点M的轨迹方程.
所成的比AM:MB=2:1,求点M的轨迹方程.
例2、过抛物线 的顶点作互相垂直的两弦OA和OB
的顶点作互相垂直的两弦OA和OB
(1)求AB中点P的轨迹方程;
(2)求抛物线顶点O在AB上射影M的轨迹方程.
例3、自抛物线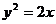 上任意一点P向其准线引垂线,垂足为Q,F为焦点,OP与FQ相交于点R,求点R的轨迹方程.
上任意一点P向其准线引垂线,垂足为Q,F为焦点,OP与FQ相交于点R,求点R的轨迹方程.
例4、设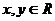 ,
, ,
, 为直角坐标平面内
为直角坐标平面内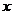 ,
,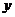 轴正方向上的单位向量,若向量
轴正方向上的单位向量,若向量 ,
, 且
且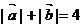 .
.
(1)求点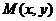 的轨迹C的方程;
的轨迹C的方程;
(2)过点(0,1)作直线 与曲线C交于A、B两点,设
与曲线C交于A、B两点,设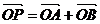 ,是否存在这样的直线
,是否存在这样的直线 ,使得四边形OAPB是矩形?若存在,求出直线
,使得四边形OAPB是矩形?若存在,求出直线 的方程;若不存在,试说明理由.
的方程;若不存在,试说明理由.
课后作业
班级_______学号__________姓名_________
1、△ABC中,A为动点,B,C为定点,B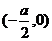 ,C
,C 且满足条件
且满足条件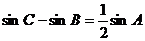 ,则动点A的轨迹方程是( )
,则动点A的轨迹方程是( )
A. B.
B.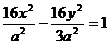 的右支
的右支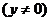
C.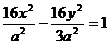 的左支
的左支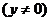 D.
D.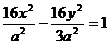

2、已知点 在以原点为圆心的单位圆上运动,则点
在以原点为圆心的单位圆上运动,则点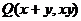 的轨迹是( )
的轨迹是( )
A.圆 B.抛物线 C.椭圆 D.双曲线
3、由动点P向圆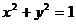 引两条切线PA,PB,切点分别是A,B,∠APB=60°则动点P的轨迹方程是______________.
引两条切线PA,PB,切点分别是A,B,∠APB=60°则动点P的轨迹方程是______________.
4、过圆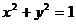 上的动点P向
上的动点P向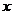 轴引垂线PQ,则线段PQ的中点M的轨迹是______________.
轴引垂线PQ,则线段PQ的中点M的轨迹是______________.
5、已知A、B是抛物线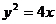 上的两个动点,并且
上的两个动点,并且 ,动点P满足
,动点P满足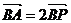 ,试求P点的轨迹方程.
,试求P点的轨迹方程.
6、点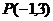 ,Q(1,3),以及直线
,Q(1,3),以及直线 :
: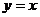 ,设AB为在直线
,设AB为在直线 上运动的长为
上运动的长为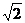 的线段,求直线PA和QB的交点M的轨迹方程.
的线段,求直线PA和QB的交点M的轨迹方程.
7、求经过点M(1,2),以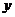 轴为准线,离心率为
轴为准线,离心率为 的椭圆的左顶点的轨迹方程.
的椭圆的左顶点的轨迹方程.
8、已知抛物线C: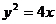 ,焦点为F,准线与
,焦点为F,准线与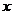 轴交于点A,过点A且斜率为
轴交于点A,过点A且斜率为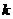 的直线
的直线 与抛物线C交于P、Q两点
与抛物线C交于P、Q两点
(1)求满足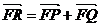 的点R的轨迹方程;
的点R的轨迹方程;
(2)若 为钝角,求直线
为钝角,求直线 的斜率
的斜率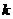 的取值范围.
的取值范围.