
例1、设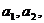

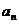 ∈R+,
∈R+,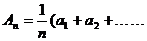
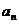 ),
),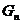 =
=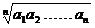
求证: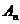 ≥
≥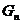 (当且仅当
(当且仅当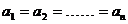 时成立)
时成立)
例2、数列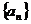 满足
满足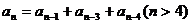 ,其前几项为1,1,2,4,6,……,数列
,其前几项为1,1,2,4,6,……,数列 定义为
定义为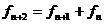 ,且
,且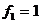 ,
,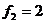 ,求证:
,求证: ,
,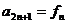 .
.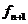
例3、m、n是正整数,求证:不定方程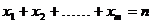 的非负整解的组数为
的非负整解的组数为
(1)选代方法
例4、(1)设 ,计算
,计算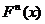 .
.
(2)设 ,计算
,计算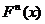 .
.
(3)设 ,计算
,计算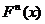 .
.
(4)设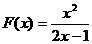 ,计算
,计算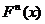 .
.
例5、设数列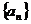 ,满足
,满足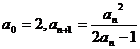 (
( =0,1,2……),求通项公式和
=0,1,2……),求通项公式和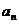 的极限.
的极限.
例6、设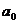 =1,
=1,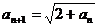 ,求证:
,求证: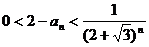
例7、已知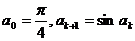 ,求证:
,求证: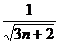 ≤
≤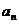 ≤
≤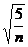
例8、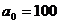 ,
, 求证:
求证: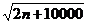 ≤
≤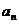 ≤
≤
(2)待定系数
例9、已知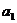 ,
, ,
, =
=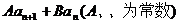 ,求
,求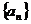 通项公式.
通项公式.
例10、已知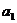 及
及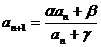 (其中
(其中 ,为常数,且
,为常数,且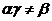 ),求
),求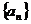 的通项.
的通项.
(3)周期数列
|
 定义在整数集上,且满足
定义在整数集上,且满足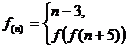
求 .
.
例12、定义数列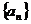 ,
,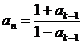 (
( ≥2,
≥2,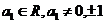 )判断数列
)判断数列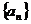 的周期性.
的周期性.
例13、设数列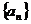 满足:
满足: ,其中
,其中 =1,2,3,……,问怎样的自然数
=1,2,3,……,问怎样的自然数 ,
,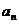 可被10整除.
可被10整除.
例14、求证:和式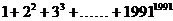 不能表示成
不能表示成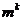 的形式,其中
的形式,其中 与
与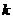 均是自然数,且
均是自然数,且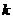 ≥2.
≥2.
例15、是否存在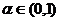 ,使得一个无穷正数列
,使得一个无穷正数列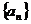 满足1+
满足1+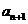 ≤
≤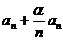 .
.
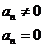 例16、对给定的
例16、对给定的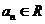 ,定义
,定义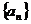 满足
满足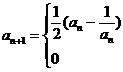
证明这个数列中有无穷多个非正项.