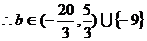1、 已知全集 ,集合
,集合 ,则
,则 等于
等于
A. B.
B. C.
C. D.
D.
2、下列函数为奇数函数的是
A. B.
B.  C.
C.  D.
D. 
3、对于直线 和平面
和平面 ,下列命题中,真命题是
,下列命题中,真命题是
A.若 ,则
,则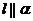 B.若
B.若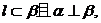 则
则
C. 若 ,则
,则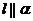 D. 若
D. 若 ,则
,则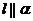
4、直线 与圆
与圆 有公共点,则常数
有公共点,则常数 的取值范围是
的取值范围是
A. B.
B.  C.
C.
 D.
D. 
5、已知命题 :
: ,则命题┐
,则命题┐ 是
是
A.  B.
B.

C.  D.
D.

6、函数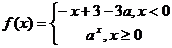 (
( )是
)是 上的减函数,则
上的减函数,则 的取值范围是
的取值范围是
A. B.
B. C.
C. D.
D. 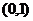
7、计算 的结果是
。
的结果是
。
8、各项均为实数的等比数列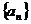 中,
中, ,则
,则 。
。
9、某校共有师生1600人,其中教师有100人,现用分层抽样的方法,从所有师生中抽取一个容量为80的样本,则抽取的学生为 。
10、已知向量 与
与 的夹角为
的夹角为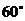 ,
, ,则
,则
 。
。
11、一只蚂蚁在三边边长分别为3,4,5的三角形的边上爬行,某时刻该蚂蚁距离三角形的三个顶点的距离均超过 的概率为 。
的概率为 。
12、根据如图所示的算法流程图,可知输出的结果 为 。
为 。
13、已知一个空间几何体的三视图如图所示,根据图中标出的尺寸(单位: ),可得这个几何体的表面积是 。
),可得这个几何体的表面积是 。
14、已知实数 满足约束条件
满足约束条件 则
则  的最小值为
。
的最小值为
。
15、设直线 的方程为
的方程为 ,将直线
,将直线 绕原点按逆时针方向旋转
绕原点按逆时针方向旋转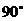 得到直线
得到直线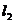 ,则
,则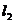 的方程是
。
的方程是
。
16、设函数 的图象位于
的图象位于 轴右侧所有的对称中心从左依次为
轴右侧所有的对称中心从左依次为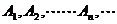 ,则
,则
 的坐标是
。
的坐标是
。
17、(本题满分12分,第1小题8分,第2小题4分)
已知函数
(1)
求函数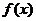 的周期;
的周期;
(2)
函数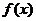 的图象可由函数
的图象可由函数 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?
18、(本题满分12分)
要建一间地面面积为20 ,墙高为
,墙高为 的长方形储藏室,在四面墙中有一面安装一扇门(门的面积和墙面的面积按一定的比例设计)。已知含门一面的平均造价为300元
的长方形储藏室,在四面墙中有一面安装一扇门(门的面积和墙面的面积按一定的比例设计)。已知含门一面的平均造价为300元 ,其余三面的造价为200元
,其余三面的造价为200元 ,屋顶的造价为250元
,屋顶的造价为250元 。问怎样设计储藏室地面矩形的长与宽,能使总价最低,最低造价是多少?
。问怎样设计储藏室地面矩形的长与宽,能使总价最低,最低造价是多少?
19、 (本题满分12分,第1小题3分,第2小题4分,第3小题5分)
(本题满分12分,第1小题3分,第2小题4分,第3小题5分)
如图,在四棱锥 中,ABCD是矩形,
中,ABCD是矩形, ,
,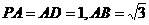 ,
,
点 是
是 的中点,点
的中点,点 在
在 上移动。
上移动。
(1)
求三棱锥 体积;
体积;
(2)
当点 为
为 的中点时,试判断
的中点时,试判断 与平面
与平面 的关系,并说明理由;
的关系,并说明理由;
(3)
求证:
20、(本题满分14分,第1小题4分,第2小题5分,第3小题5分)
已知各项均为正数的数列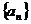 中,
中, 是数列
是数列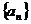 的前
的前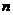 项和,对任意
项和,对任意 ,有
,有

(1)
求常数 的值;
的值;
(2)
求数列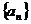 的通项公式;
的通项公式;
(3)
记 ,求数列
,求数列 的前
的前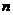 项和
项和 。
。
21、(本题满分14分,第1小题5分,第2小题9分)
 如图,椭圆
如图,椭圆 的左、右焦点为
的左、右焦点为 ,过
,过 的直线
的直线 与椭圆相交于
与椭圆相交于 、
、 两点。
两点。
(1)
若 ,且
,且
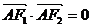 求椭圆的离心率。
求椭圆的离心率。
(2)
若 ,求
,求 的最大值和最小值。
的最大值和最小值。
22、(本题满分16分,第1小题8分,第2小题8分)
设函数 ,
, ,当
,当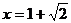 时,
时,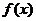 取得极值。
取得极值。
(1)
求 的值,并判断
的值,并判断 是函数
是函数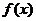 的极大值还是极小值;
的极大值还是极小值;
(2)
当 时,函数
时,函数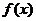 与
与 的图象有两个公共点,求
的图象有两个公共点,求 的取值范围。
的取值范围。
高三数学上学期质量检测试题参考答案
参考答案
一、选择题(本大题共6小题,每小题5 分,共30分)
ABDADB
二、填空题(本大题共10小题,每小题5分,共50分,把答案填在题中横线上)
7、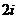 ;8、
;8、 ;9、75;10、
;9、75;10、 ;11、
;11、 ;12、11;13、
;12、11;13、 ;
;
14、 ;15、
;15、 ;16、
;16、
三、解答题
17、解:(1)

所以 函数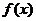 的周期是
的周期是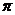 ………………………………………………8分
………………………………………………8分
(2)将函数 的图象向左平移
的图象向左平移 个单位,再将所得图象上每一点的横坐标变为原来的
个单位,再将所得图象上每一点的横坐标变为原来的 倍(纵坐标不变式),得函数
倍(纵坐标不变式),得函数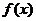 的图象………………………12分。
的图象………………………12分。
18、解:设地面矩形在门正下方的一边长为 ,则另一边的长为
,则另一边的长为 ………2分
………2分
设总造价为 元,则
元,则
 …………………………………………………………………………………7分
…………………………………………………………………………………7分
因为 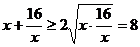
当且仅当 (
( 即
即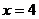 时 取“=”…………………………9分
时 取“=”…………………………9分
所以,当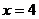 时
时 有最小的值
有最小的值 此时
此时 ……………………11分
……………………11分
答:当储藏室地面矩形在门正下方的一边长为 ,另一边的长为
,另一边的长为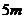 时,能使总造价最低造价为17000元。……………………………………………………12分。
时,能使总造价最低造价为17000元。……………………………………………………12分。
19、解:(1)
 ,
,

 …………3分
…………3分
(2)当点 为
为 的中点时,
的中点时, 。…………4分
。…………4分
理由如下: 点
点 分别为
分别为 、PD的中点,
、PD的中点,

 。
。

 ,
,
 …………………………………………7分
…………………………………………7分
(3)
 ,
,

 ,
,
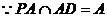 ,
,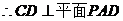

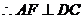 …………………………………10分
…………………………………10分
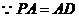 ,点
,点 是
是 的中点
的中点 
又
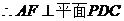

 ………………………………12分
………………………………12分
20、解:(1)由 及
及 ,得:
,得:
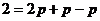
 ……………………………………………………4分
……………………………………………………4分
(2)由 ①
①
得 ②
②
由②-①,得 
即: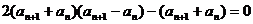

由于数列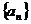 各项均为正数,
各项均为正数,
 即
即  ……………………………………6分
……………………………………6分
 数列
数列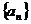 是首项为
是首项为 ,公差为
,公差为 的等差数列,
的等差数列,
 数列
数列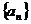 的通项公式是
的通项公式是  ……………9分
……………9分
(3)由 ,得:
,得:
 ……………………………………………………11分
……………………………………………………11分
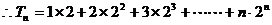



21、解:(1)
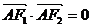 ,
,

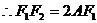 ,
, …………………………3分
…………………………3分
 ,
,
 ………………………………………5分
………………………………………5分
(2) ,
, 。
。
①若 垂直于
垂直于 轴,则
轴,则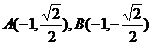 ,
,
 ,
,

②若 与
与 轴不垂直,设直线
轴不垂直,设直线 的斜率为
的斜率为 ,则直线
,则直线 的方程为
的方程为

由 得
得 
 ,
, 方程有两个不等的实数根。
方程有两个不等的实数根。
设 ,
, .
.
 ,
,  ………………………………9分
………………………………9分
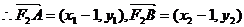



= ……………………………………12分
……………………………………12分
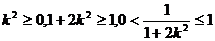 …………………………………13分
…………………………………13分
 ,所以当直线
,所以当直线 垂于
垂于 轴时,
轴时, 取得最大值
取得最大值
当直线 与
与 轴重合时,
轴重合时, 取得最小值
取得最小值 …………………………14分
…………………………14分
22、解:(1)由题意
 ………………………………………………2分
………………………………………………2分
 当
当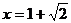 时,
时,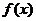 取得极值,
取得极值,
 所以
所以


 即
即 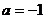 …………………………5分
…………………………5分
此时当 时,
时, ,当
,当 时,
时,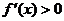 ,
,
 是函数
是函数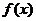 的最小值。………………………………………8分
的最小值。………………………………………8分
(2)设 ,则
,则  ,
,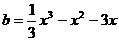 ……10分
……10分
设 ,
,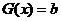
 ,令
,令 解得
解得 或
或
列表如下:
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
 |
 |
__ |
0 |
+ |
|
 |
 |
 |
 |
 |
 |
 |
 |
 函数
函数 在
在 和
和 上是增函数,在
上是增函数,在 上是减函数。
上是减函数。
当 时,
时, 有极大值
有极大值 ;当
;当 时,
时, 有极小值
有极小值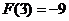 ……14分
……14分
 函数
函数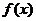 与
与 的图象有两个公共点,
的图象有两个公共点, 函数
函数 与
与 的图象有两个公共点
的图象有两个公共点
 或
或