
1、
 是直线
是直线 和直线
和直线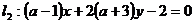 垂直的( )
垂直的( )
 充分条件
充分条件  必要条件
必要条件
 充要条件
充要条件  既非充分也非必要条件
既非充分也非必要条件
2、已知直线 与过点
与过点 的直线交于
的直线交于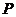 点,则
点,则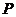 分有向线段
分有向线段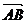 的比为 ( )
的比为 ( )








3、直线 在
在 轴、
轴、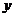 轴上的截距分别是
轴上的截距分别是 和
和 ,直线
,直线 的方程是
的方程是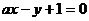 ,若直线
,若直线 到
到 的角是
的角是 ,则
,则 的值为 ( )
的值为 ( )

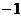

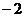



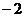 和
和
4、若方程 仅表示一条直线,则
仅表示一条直线,则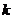 的取值范围是( )
的取值范围是( )

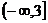

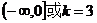

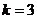


5.已知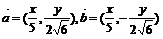 ,双曲线
,双曲线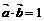 上一点M到F(7,0)的距离为11,N是MF的中点,O为坐标原点,则|ON|=( )
上一点M到F(7,0)的距离为11,N是MF的中点,O为坐标原点,则|ON|=( )
 、
、
 、
、
 、
、
 、
、
6、已知 是椭圆
是椭圆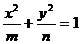 的两个焦点,P是椭圆上的点,当
的两个焦点,P是椭圆上的点,当 的面积最大,则有( )
的面积最大,则有( )







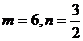
7、 . 如图所示,在正方体
. 如图所示,在正方体 的侧面
的侧面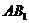 内有一动点
内有一动点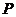 到直线
到直线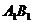 和直线
和直线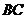 的距离相等,则动点
的距离相等,则动点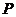 所在曲线形状为 ( )
所在曲线形状为 ( )
A B
C D
8、已知圆锥曲线 的离心率e为方程
的离心率e为方程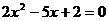 的两根,则满足条件的圆锥曲线的条数为
( )
的两根,则满足条件的圆锥曲线的条数为
( )
 1
1  2
2
 3
3
 4
4
9、双曲线C的一个顶点到相应的准线的距离与这个顶点到另一个焦点的距离之比为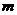 ,则
,则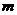 的取值范围是( )
的取值范围是( )

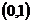

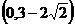




10、过椭圆左焦点 且倾斜角为60°的直线交椭圆于
且倾斜角为60°的直线交椭圆于 两点,若
两点,若 ,则椭圆的离心率等于 ( )
,则椭圆的离心率等于 ( )








11、已知向量 ,
,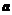 与
与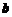 的夹角为
的夹角为 ,则直线
,则直线
 与圆
与圆 的位置是( )
的位置是( )
 相切
相切
 相交
相交  相离
相离  随
随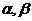 的值而定
的值而定
12、已知点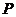 在双曲线
在双曲线 的右支上,
的右支上, 是双曲线两个焦点,则△
是双曲线两个焦点,则△ 的内切圆的圆心的横坐标是( )
的内切圆的圆心的横坐标是( )

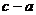





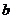
13、与圆 相切,且在两坐标轴上的截距相等的直线方程为
。
相切,且在两坐标轴上的截距相等的直线方程为
。
14、圆锥曲线 的一个焦点是
的一个焦点是 ,相应的准线方程为
,相应的准线方程为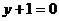 ,且曲线
,且曲线 经过点
经过点 ,则曲线
,则曲线 的形状是
。
的形状是
。
15、13、E,F是椭圆 的左、右焦点,
的左、右焦点,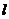 是椭圆的一条准线,点P在
是椭圆的一条准线,点P在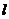 上,则角
上,则角 的最大值是 。
的最大值是 。
16、正三角形 中,
中, 的中点,则以
的中点,则以 为焦点且过
为焦点且过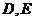 的双曲线的离心率是 。
的双曲线的离心率是 。
17、直线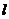 经过两条直线
经过两条直线 :
: 和
和
 的交点,且分这两条直线与
的交点,且分这两条直线与 轴围成的面积为
轴围成的面积为 两部分,求直线
两部分,求直线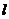 的一般式方程。
的一般式方程。
18、设直线 与圆
与圆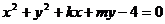 交于
交于 两点,且
两点,且 关于
关于
直线 对称,求不等式组
对称,求不等式组 表示平面区域的面积。
表示平面区域的面积。
19、 如果探照灯的轴截面是抛物线
如果探照灯的轴截面是抛物线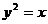 (如图),表示平行于对称轴
(如图),表示平行于对称轴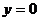 的光线经抛物线上的点
的光线经抛物线上的点 的反射情况,设点
的反射情况,设点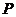 的纵坐标为
的纵坐标为 ,当
,当 取何值时,从入射点
取何值时,从入射点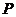 到反射点
到反射点 的光线路程
的光线路程 最短?
最短?
|
20、已知中心在原点,焦点在x轴上的椭圆的离心率为 ,
, 为其焦点,一直线过点
为其焦点,一直线过点 与椭圆相交于
与椭圆相交于 两点,且
两点,且 的最大面积为
的最大面积为 ,求椭圆的方程。
,求椭圆的方程。
21、设抛物线 ,若椭圆
,若椭圆 的左焦点
的左焦点 和相应的准线
和相应的准线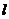 分别与抛物线的焦点和准线重合。椭圆的短轴的一个端点为
分别与抛物线的焦点和准线重合。椭圆的短轴的一个端点为 ,且线段
,且线段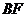 的中点
的中点 到定点
到定点 的距离的最小值为
的距离的最小值为 ,试求实数
,试求实数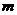 的值以及此时的椭圆方程。
的值以及此时的椭圆方程。
22、已知椭圆 与射线y=
与射线y=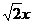 (x
(x 交于点A,过A作倾斜角互补的两条直线,它们与椭圆的另一个交点分别为点B和点C。
交于点A,过A作倾斜角互补的两条直线,它们与椭圆的另一个交点分别为点B和点C。
(1)求证:直线BC的斜率为定值,并求这个定值。
第六章 直线与圆锥曲线单元测试卷 班级________ 学号________ 姓名____________ 得分________参考答案
(2)求三角形ABC的面积最大值。
解几单元试卷参考答案
一、选择题:
1、A 2、C 3、B 4、D 5、B 6、A
7、C 8、C 9、B 10、D 11、C 12、B
二、填空题:
13、 14、椭圆
14、椭圆
15、 16、
16、
三、 解答题:
解答题:
17:解:由
得两直线交点的坐标 ,
,
又由题意知S1:S2=2:3或3:2
所以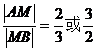 由A (-4,0),B(6,0) 根据定比分点公式得
由A (-4,0),B(6,0) 根据定比分点公式得
M(0,0)或M(2,0),所以所求直线的方程就是经过P和M两点的直线方程
所以所求直线的一般式方程是
18: 解:由题意直线 与圆
与圆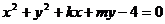 交于
交于 两点,且
两点,且 关于直线
关于直线 对称,则
对称,则 与
与 两直线垂直,可求出
两直线垂直,可求出 ,又不等式组所表示的平面区域应用线线规划去求,易得面积为
,又不等式组所表示的平面区域应用线线规划去求,易得面积为
19、解:设 ,则直线
,则直线 方程为:
方程为: ,由
,由
得 ,当且仅当
,当且仅当
当入射点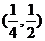 ,反射点
,反射点 时
时 最短。
最短。
20、解:由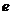 =
= 得
得 ,所以椭圆方程设为
,所以椭圆方程设为
设直线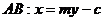 ,由
,由 得:
得:
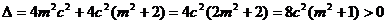
设 ,则
,则 是方程的两个根
是方程的两个根
由韦达定理得 所以
所以


=
当且仅当 时,即
时,即 轴时取等号
轴时取等号 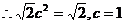
所以,所求椭圆方程为
21、解:已知焦点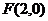 ,准线
,准线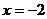 ,设椭圆半焦距为
,设椭圆半焦距为 ,半短轴长为
,半短轴长为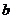 ,
,
椭圆中心 ,又
,又 即
即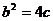

①当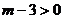 即
即 时,此时
时,此时


②当 时,即
时,即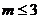 ,此时由于
,此时由于 ,所以
,所以 无最小值。
无最小值。
所以,所求 此时椭圆方程为
此时椭圆方程为 。
。
22、解:(!)由题意得 ,设
,设 的斜率为
的斜率为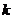 ,则
,则 的斜率为-
的斜率为-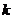
所以 代入得
代入得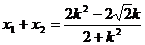 ,又
,又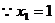
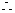
 同理
同理
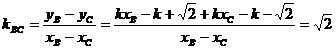 为定值
为定值
(1)设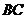 方程为
方程为
 得
得
 得
得
 到
到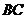 的距离为
的距离为
所以
当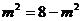 时,即
时,即 时“=”成立,此时
时“=”成立,此时 成立。
成立。