
1.设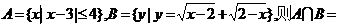 ( )
( )
A.{0} B.{2} C.φ D.{x|2≤x≤7}
2.要完成下列2项调查:①从某社区125户高收入家庭,280户中等收入家庭,95户低收入家庭中选出100户调查社会购买力的某项指标;②从某中学高一年级的12名体育特长生中选出3人调查学习负担情况。应采用的抽样方法是 ( )
A.①用随机抽样法 ②用系统抽样法
B.①用分层抽样法 ②用随机抽样法
C.①用系统抽样法 ②用分层抽样法
D.①、②都用分层抽样法
3.设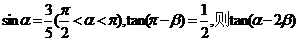 的值等于 ( )
的值等于 ( )
A.-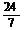 B.-
B.-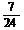 C.
C.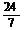 D.
D.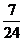
4. 等比数列{ an }中,a2、a10是方程x2 -5x+9 = 0的两根,则a6= A.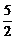 B.5
C.9 D.±3
B.5
C.9 D.±3
5.已知xy<0且x+y=2,而(x+y)7按x的降幂排列的展开式中,第三项不大于第四项,那么 x的取值范围是 ( )
A.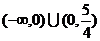 B.
B.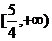 C.
C.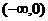 D.
D.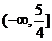
6.给出下面的3个命题:(1)函数 的最小正周期是
的最小正周期是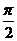 ;(2)函数
;(2)函数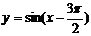 在区间
在区间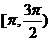 上单调递增;
上单调递增;
(3)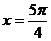 是函数
是函数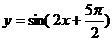 的图象的一条对称轴.
的图象的一条对称轴.
其中正确命题的个数是 ( )
A.0 B.1 C.2 D.3
7.以椭圆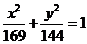 的右焦点为圆心,且与双曲线
的右焦点为圆心,且与双曲线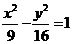 的渐近线相切的圆的方
程是 ( )
的渐近线相切的圆的方
程是 ( )
A.x2+y2-10x+9=0 B.x2+y2-10x-9=0
C.x2+y2+10x+9=0 D.x2+y2+10x-9=0
8.已知直线l⊥平面α,直线m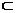 平面β,有下面四个命题:
平面β,有下面四个命题:
①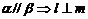 ;②
;②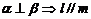 ; ③
; ③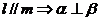 ;④
;④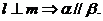 其中正确的两个命题是 ( )
其中正确的两个命题是 ( )
A.①与② B.①与③ C.②与④ D.③与④
9.抛物线y2=2px与直线ax+y-4=0交于两点A、B,其中点A的坐标是(1,2).设抛物线 的焦点为F,则|FA|+|FB|等于 ( )
A.7
B.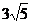 C.6 D.5
C.6 D.5
10.三棱柱ABC-A1B1C1中,P、Q分别为侧棱AA1、BB1上的点,且A1P=BQ,则四棱锥C1-APQB与三棱柱ABC-A1B1C1的体积之比是 ( )
A.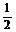 B.
B.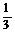 C.
C.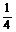 D.
D.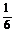
11.曲线f(x)=x3+x-2在P0点处的切线平行于直线y=4x-1,则P0点的坐标为( )
A.(1,0) B.(2,8)
C.(1,0)和(-1,-4) D.(2,8)和(-1,-4)
12.已知f(x)=3x-b(2≤x≤4,b为常数)的图象经过点(2,1),则F(x)=[f-1(x)]2-f-1(x2)的值域为 ( )
A.[2,5] B.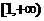 C.[2,10] D.[2,13]
C.[2,10] D.[2,13]
13.在条件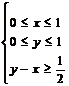 下,W=4-2x+y的最大值是
.
下,W=4-2x+y的最大值是
.
14.已知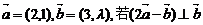 ,则λ的值是 .
,则λ的值是 .
15.正方形ABCD中,E、F分别是AB、CD的中点,沿EF将正方形折成60°的二面角,则异面直线BF与DE所成角的余弦值是 .
16.给出下列四个命题:
(1)函数y=ax(a>0且a≠1)与函数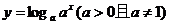 的定义域相同:
的定义域相同:
(2)函数y=x3与y=3x的值域相同;
(3)函数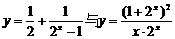 都是奇函数;
都是奇函数;
(4)函数y=(x-1)2与y=2x-1在区间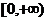 上都是增函数.
上都是增函数.
其中正确命题的序号是 .(把你认为正确的命题序号都填上).
17.(12分)甲、乙、丙三位同学独立完成6道数学自测题,他们答及格的概率依次为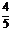 、
、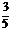 、
、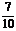 .求(1)三人中有且只有2人答及格的概率;(2)三人中至少有一人不及格的概率.
.求(1)三人中有且只有2人答及格的概率;(2)三人中至少有一人不及格的概率.
18.(12分)将函数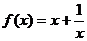 的图象向右平移4个单位,再向上平移2个单位,可得到函数g(x)的图象.(1)写出g(x)的解析式;(2)解关于x的不等式
的图象向右平移4个单位,再向上平移2个单位,可得到函数g(x)的图象.(1)写出g(x)的解析式;(2)解关于x的不等式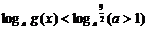 .
.
19.(12分)已知数列{an}的前n项和为Sn,且满足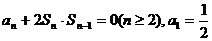 .
.
(1)求证:{ }是等差数列;(2)求an的表达式;
}是等差数列;(2)求an的表达式;
(3)若bn=2(1-n).an(n≥2)时,求证:b22+b32+…+bn2<1.
20.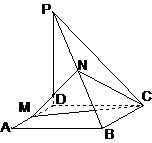 (12分)已知ABCD是矩形,PD⊥平面ABCD,PD=DC=a,AD=
(12分)已知ABCD是矩形,PD⊥平面ABCD,PD=DC=a,AD=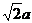 ,M、N分别是AD、PB的中点.
,M、N分别是AD、PB的中点.
(1) 求证:平面MNC⊥平面PBC;
(2)求点A到平面MNC的距离.
21.(12分)某公司欲将一批不易存放的水果从A地运往B地,有汽车、火车、直升飞机等运输工具可供选择,三种运输工具的主要参考数据如下:
|
运输工具 |
速度(千米/时) |
途中费用(元/千米) |
装卸时间(小时) |
装卸费用(元) |
|
汽 车 |
50 |
8 |
2 |
1000 |
|
火 车 |
100 |
4 |
4 |
2000 |
|
飞 机 |
200 |
16 |
2 |
1000 |
若这批水果在运输过程中(含装卸时间)的损耗为300元/时,问采用哪一种运输工具较好(即运输过程中费用与损耗之和最小)?
22.(14分)已知椭圆C的焦点是F1(-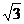 ,0)、F2(
,0)、F2(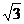 ,0),点F1到相应的准线的距离为
,0),点F1到相应的准线的距离为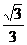 ,过F2点且倾斜角为锐角的直线l与椭圆C交于A、B两点,使得|F2B|=3|F2A|.
,过F2点且倾斜角为锐角的直线l与椭圆C交于A、B两点,使得|F2B|=3|F2A|.
(1)求椭圆C的方程;(2)求直线l的方程.
2007卫华高中高考仿真试题(文科数学)参考答案
高考模拟测试数学参考答案及评分意见
一、选择题(5分×12=60分)
1.A 2.B 3.D 4.D 5.C 6.C 7.A 8.B 9.A 10.B 11.C 12.C
二、填空题(4分×4=16分)
13.5 14.λ=-1或λ=3 15. 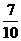 16.(1)(3)
16.(1)(3)
三、解答题(共74分)
17.解:(文)设甲、乙、丙答题及格分别为事件A、B、C,则事件A、B、C相互独立………………2分
(1)三人中有且只有2人答及格的概率为
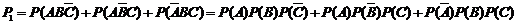
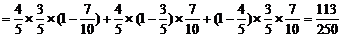 ……7分
……7分
(2)三人中至少有一人不及格的概率为P2=1-P(ABC)=1-P(A)P(B)P(C)=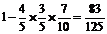 12分
12分
18.解:(1)依题意,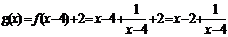 .4分
.4分
(2)不等式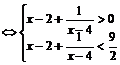 …6分
…6分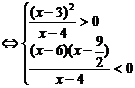
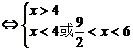 …10分
…10分
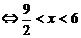 ………………11分
………………11分
∴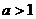 时,不等式解集为
时,不等式解集为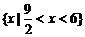 …………12分
…………12分
19.(1)证明: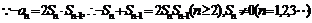 …1分
…1分
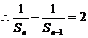 ……2分
又
……2分
又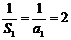
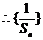 是以2为首项,2为公差的等差数列……4分
是以2为首项,2为公差的等差数列……4分
(2)
解:由(1)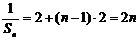
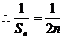 …5分
当n≥2时,
…5分
当n≥2时,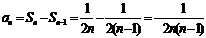
(3)
(或n≥2时,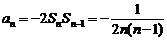 )
)
当n=1时,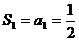 …………7分
…………7分
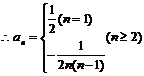 ………………8分
………………8分
(3)由(2)知,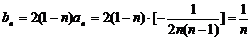 …………………9分
…………………9分
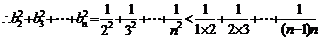 …10分
…10分
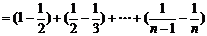 ……11分
……11分
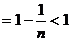 ………………12分
………………12分
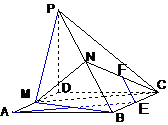 20.解:(1)连PM、MB ∵PD⊥平面ABCD ∴PD⊥MD…1分
20.解:(1)连PM、MB ∵PD⊥平面ABCD ∴PD⊥MD…1分
 ∴PM=BM 又PN=NB
∴PM=BM 又PN=NB
∴MN⊥PB………3分
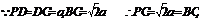 得
得
NC⊥PB∴PB⊥平面MNC……5分
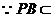 平面PBC
平面PBC
∴平面MNC⊥平面PBC……6分
(2)取BC中点E,连AE,则AE//MC∴AE//平面MNC,
A点与E点到平面MNC的距离相等…7分
取NC中点F,连EF,则EF平行且等于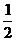 BN
∵BN⊥平面MNC ∴EF⊥平面MNC,EF长为E
BN
∵BN⊥平面MNC ∴EF⊥平面MNC,EF长为E
点到平面MNC的距离……9分 ∵PD⊥平面ABCD,BC⊥DC ∴BC⊥PC.
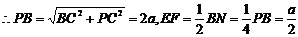 即点A到平面MNC的距离为
即点A到平面MNC的距离为 ……12分
……12分
21.解:设A、B两地的距离为S千米,分别用F1、F2、F3表示汽车、火车、飞机运输时的总支出…1分
则有F1=8S+1000+300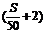 =14S+1600(元) F2=4S+2000+300
=14S+1600(元) F2=4S+2000+300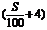 =7S+3200(元)
=7S+3200(元)
F3=16S+1000+300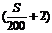 =17.5S+1600(元)……7分 ∵S>0,∴F1<F3 由F1-F2=7S-1600
=17.5S+1600(元)……7分 ∵S>0,∴F1<F3 由F1-F2=7S-1600
∴当0<S<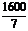 千米时F1<F2,F1最小,采用汽车运输较好;……10分
千米时F1<F2,F1最小,采用汽车运输较好;……10分
当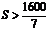 千米时F2<F1<F3,采用火车运输较好;
千米时F2<F1<F3,采用火车运输较好;
当S= 千米时,采用汽车与火车运输的费用一样,但比飞机运输费用少.……………………12分
千米时,采用汽车与火车运输的费用一样,但比飞机运输费用少.……………………12分
22.解(1)依题意,椭圆中心为O(0,0),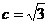 …1分
…1分
点F1到相应准线的距离为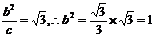 ,
,
 a2=b2+c2=1+3=4…………3分
a2=b2+c2=1+3=4…………3分
∴所求椭圆方程为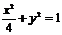 ……4分
……4分
(2)设椭圆的右准线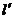 与l交于点P,作AM⊥
与l交于点P,作AM⊥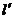 ,AN⊥
,AN⊥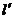 ,垂足
,垂足
分别为M、N. 由椭圆第二定义,得
同理|BF2|=e|BN|……6分 由Rt△PAM-Rt△PBN,得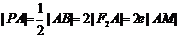 …9分
…9分
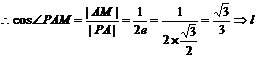 的斜率
的斜率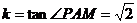 .………………12分
.………………12分
∴直线l的方程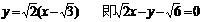 ………14分
………14分