
1.已知集合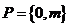 ,
,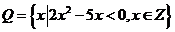 ,若
,若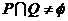 ,则
,则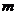 等于( )
等于( )
A. 1 B.
2 C. 1或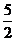 D. 1或2
D. 1或2
2.已知等差数列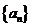 前17项和
前17项和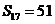 ,则
,则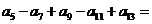 ( )
( )
A. 3 B. 6 C. 17 D. 51
3.设随机变量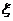 服从正态分布
服从正态分布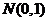 ,若
,若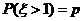 ,则
,则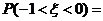 ( )
( )
A. 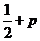 B.
B.
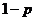 C.
C.
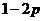 D.
D.
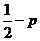
4.把函数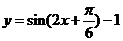 的图象按向量
的图象按向量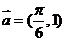 平移,再把所得图象上各点的横坐标缩短为原来的
平移,再把所得图象上各点的横坐标缩短为原来的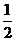 ,则所得图象的函数解析式是(
)
,则所得图象的函数解析式是(
)
A. 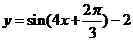 B.
B.

C. 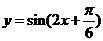 D.
D.
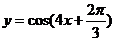
5.二项式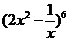 的展开式中,常数项为( )
的展开式中,常数项为( )
A. 30 B. 48 C. 60 D. 120
6.设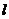 、
、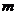 是两条不同的直线,
是两条不同的直线,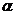 、
、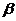 是两个不同的平面,则下列正确的是( )
是两个不同的平面,则下列正确的是( )
A. 若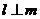 ,
,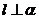 ,则
,则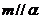 B.
若
B.
若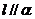 ,
,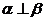 ,则
,则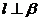
C. 若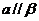 ,
,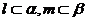 ,则
,则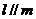 D. 若
D. 若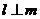 ,
,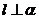 ,
,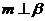 ,则
,则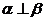
7.口袋中放有大小相等的两个红球和一个白球,有放回地每次摸取一个球,定义数列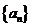 ,
,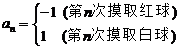 ,如果
,如果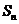 为数列
为数列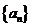 的前
的前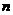 项和,那么
项和,那么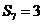 的概率为( )
的概率为( )
A. 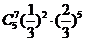 B.
B. 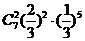 C.
C.
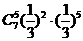 D.
D. 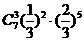
8.若第一象限内的点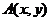 落在经过点
落在经过点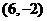 且具有方向向量
且具有方向向量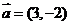 的直线
的直线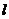 上,则
上,则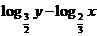 有( )
有( )
A.
最大值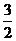 B. 最大值1 C. 最小值
B. 最大值1 C. 最小值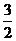 D.
最小值1
D.
最小值1
9.已知点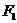 、
、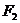 为双曲线
为双曲线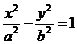 (a>0,b>0) 的左、右焦点,P为右支上一点,点P到右准线的距离为d,若|P
(a>0,b>0) 的左、右焦点,P为右支上一点,点P到右准线的距离为d,若|P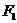 |、|P
|、|P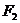 |、d依次成等差数列,则此双曲线离心率取值范围是( )
|、d依次成等差数列,则此双曲线离心率取值范围是( )
A. 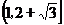 B. (1,
B. (1,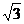 ]
C. [2+
]
C. [2+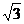 ,+
,+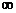 )
D. [2-
)
D. [2-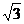 ,2+
,2+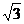 ]
]
10.已知函数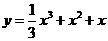 的图象C上存在一定点P满足:若过点P的直线
的图象C上存在一定点P满足:若过点P的直线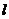 与曲线C交于不同于P的两点
与曲线C交于不同于P的两点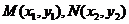 ,且恒有
,且恒有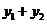 为定值
为定值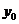 ,则
,则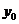 的值为( )
的值为( )
A. 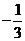 B.
B.
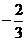 C.
C.
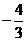 D.
D.
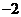
第Ⅱ卷(非选择题 共100分)
11.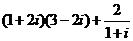 = ____
= ____
12.已知实数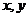 满足
满足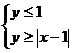 ,则
,则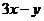 的最大值是 _____
的最大值是 _____
13.已知定义在R上的函数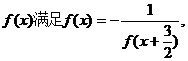
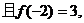 则
则
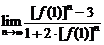 的值等于___________
的值等于___________
14.表面积为4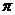 的球O与平面角为钝角的二面角的两个半平面相切于A、B两点,三角形OAB的面积
的球O与平面角为钝角的二面角的两个半平面相切于A、B两点,三角形OAB的面积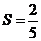 ,则球心到二面角的棱的距离为 ______ _
,则球心到二面角的棱的距离为 ______ _
15.已知椭圆C: ,
,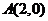 为长轴的一个端点,弦BC过椭圆的中心O,且
为长轴的一个端点,弦BC过椭圆的中心O,且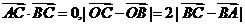 ,则椭圆的离心率为 _______
,则椭圆的离心率为 _______
16.设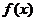 是定义域为R的奇函数,
是定义域为R的奇函数,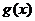 是定义域为R的恒大于零的函数,且当
是定义域为R的恒大于零的函数,且当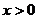 时有
时有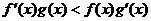 .若
.若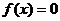 ,则不等式
,则不等式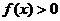 的解集是___________
的解集是___________
17.(13分)设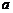 、
、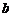 、
、 分别是△ABC三个内角
分别是△ABC三个内角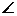 A、
A、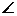 B、
B、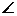 C的对边,若向量
C的对边,若向量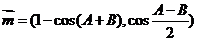 ,
,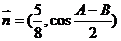 且
且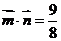 ,
,
(1)求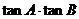 的值;
的值;
(2)求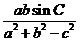 的最大值.
的最大值.
18.(13分)甲乙两人进行一场乒乓球比赛,根据以往经验单局比赛甲胜乙的概率为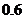 ,本场比赛采用五局三胜制。既先胜三局的人获胜,比赛结束。设每局比赛相互间没有影响,令
,本场比赛采用五局三胜制。既先胜三局的人获胜,比赛结束。设每局比赛相互间没有影响,令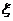 为本场比赛甲胜乙的局数(不计甲负乙的局数)。
为本场比赛甲胜乙的局数(不计甲负乙的局数)。
(1)求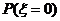 ;
;
(2)求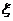 的概率分布和数学期望。(精确到
的概率分布和数学期望。(精确到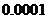 )
)
19.(13分)如图,在各棱长均为2的三棱柱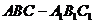 中,侧面
中,侧面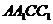 ⊥底面
⊥底面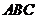 ,
,
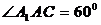
(1) 求侧棱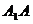 与平面
与平面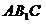 所成角的大小;
所成角的大小;
(2) 已知点D满足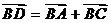 ,在直线AA
,在直线AA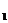 上是否存在点P,使
上是否存在点P,使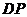 ∥平面
∥平面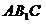 ?
?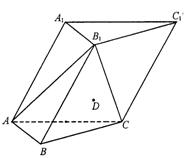 若存在,请确定点P的位置;若不存在,请说明理由.
若存在,请确定点P的位置;若不存在,请说明理由.
20.(13分)四棱锥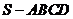 的所有棱长均为1米,一只小虫从
的所有棱长均为1米,一只小虫从 点出发沿四棱锥爬行,若在每一顶点处选择不同的棱都是等可能的。设小虫爬行
点出发沿四棱锥爬行,若在每一顶点处选择不同的棱都是等可能的。设小虫爬行 米后恰回到
米后恰回到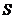 点的概率为
点的概率为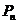 。
。
 (1)求
(1)求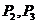 的值;
的值;
(2)求证: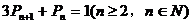 ;
;
(3)
求证: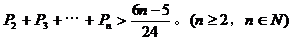
21.(12分)已知抛物线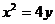 ,过点
,过点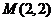 作动弦
作动弦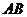 ,过
,过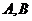 两点分别作抛物线的切线,两切线交于点
两点分别作抛物线的切线,两切线交于点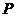
(1)证明:点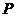 的轨迹为直线
的轨迹为直线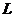 ,并求出
,并求出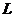 的方程;
的方程;
(2)过点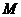 作直线
作直线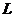 的垂线,垂足为
的垂线,垂足为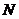 ,证明:
,证明: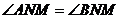
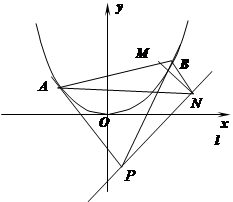
22.(12分)设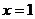 是函数
是函数 的一个极值点(
的一个极值点(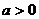 ,e为自然对数的底).
,e为自然对数的底).
(1)求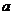 与
与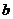 的关系式(用
的关系式(用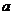 表示
表示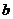 ),并求
),并求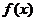 的单调区间;
的单调区间;
(2)若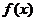 在闭区间
在闭区间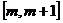 上的最小值为0,最大值为
上的最小值为0,最大值为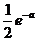 ,且
,且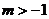 。试求m与
。试求m与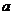 的值.
的值.
11. 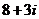 12.5 13.
12.5 13.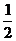
14. 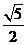 15.
15. 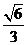 16.
16. 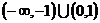
17.解:(1) 由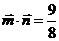 ,得
,得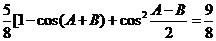
即 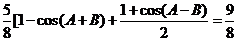
亦即 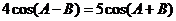
所以 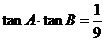
(2) 因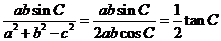
而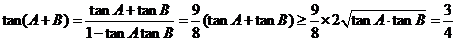
所以,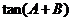 有最小值
有最小值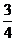
当 时,取得最小值。又
时,取得最小值。又 ,则
,则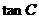 有最大值
有最大值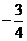
故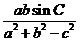 的最大值为
的最大值为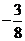
18. 解:(Ⅰ)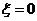 即表示本场比赛共三局,甲连负三局
即表示本场比赛共三局,甲连负三局
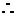
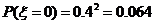
(Ⅱ)甲胜乙的局数作为随机变量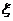 ,其取值有
,其取值有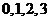 四个值
四个值
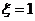 时,本场比赛共四局,第一,二、三局中甲胜一局,甲负第四局
时,本场比赛共四局,第一,二、三局中甲胜一局,甲负第四局
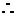

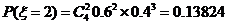
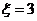 时,本场比赛或三局,和四局,或五局,甲胜
时,本场比赛或三局,和四局,或五局,甲胜
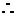
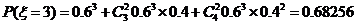
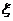 的概率分布列为
的概率分布列为
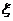 |
0 |
1 |
2 |
3 |
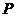 |
 |
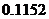 |
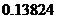 |
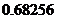 |
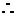
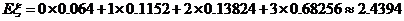
(注: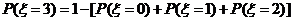 来计算)
来计算)
19. 解:∵侧面A1ACC1⊥底面ABC,作A1O⊥AC于点O,
∴A1O⊥平面ABC.
又∠ABC=∠A1AC=60°,且各棱长都相等,
∴AO=1,OA1=OB=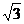 ,BO⊥AC.
,BO⊥AC.
故以O为坐标原点,建立如图所示的空间直角坐标系O-xyz,则
A(0,-1,0),B(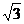 ,0,0),A1(0,0,
,0,0),A1(0,0,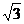 ),C(0,1,0),
),C(0,1,0),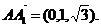
∴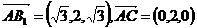 .
.
设平面AB1C的法向量为n=(x,y,1)
则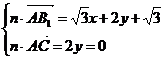 解得n=(-1,0,1).
解得n=(-1,0,1).
由cos<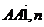 >=
>=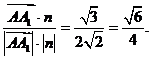
而侧棱AA1与平面AB1C所成角,即是向量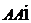 与平面AB1C的法向量所成锐角的余角,
与平面AB1C的法向量所成锐角的余角,
∴侧棱AA1与平面AB1C所成角的大小为arcsin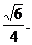
(Ⅱ) ∵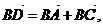 而
而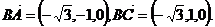
∴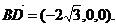
又∵B(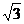 ,0,0),∴点D的坐标为D(-
,0,0),∴点D的坐标为D(-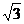 ,0,0).
,0,0).
假设存在点P符合题意,则点P的坐标可设为P(0,y,z).
∴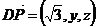
∵DP∥平面AB1C,n=(-1,0,1)为平面AB1C的法向量,
∴由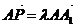 ,得
,得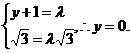 又DP
又DP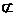 平面AB1C,
平面AB1C,
故存在点P,使DP∥平面AB1C,其从标为(0,0,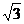 ),即恰好为A1点.
),即恰好为A1点.
20.解:(I)P2表示从S点到A(或B、C、D),然后再回到S点的概率
所以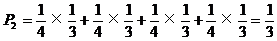 ;
;
因为从S点沿SA棱经过B或D,然后再回到S点的概率为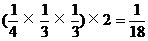 ,
,
所以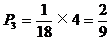
(II)设小虫爬行n米后恰回到S点的概率为Pn,那么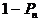 表示爬行n米后恰好没回到S点的概率,则此时小虫必在A(或B、C、D)点
表示爬行n米后恰好没回到S点的概率,则此时小虫必在A(或B、C、D)点
所以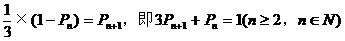
(III)由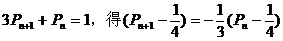
从而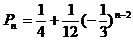
所以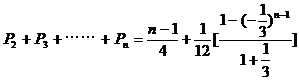
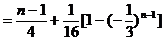
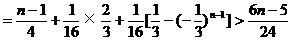
21.解(1)设A,B两点的坐标为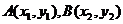 则有
则有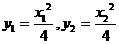 于是
于是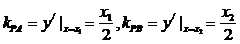 ,由点斜式求得两切线方程:
,由点斜式求得两切线方程:
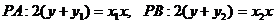 解得P的坐标为
解得P的坐标为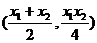
由A,M,B三点共线得: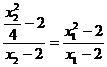 ,
,
即: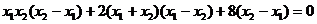 ,由
,由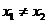 故有
故有
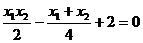 ,故P的轨迹方程为
,故P的轨迹方程为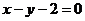
(2)过点M所作垂线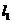 的方程为
的方程为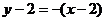 ,即
,即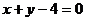 从而交点
从而交点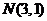
MN的斜率为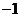 ,若AN,BN的斜率存在,则设为
,若AN,BN的斜率存在,则设为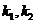 。要证
。要证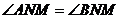 ,只需证
,只需证
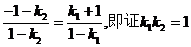 ,而
,而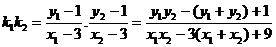
设直线AB的斜率为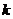 则由:
则由: 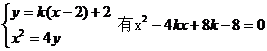
所以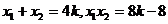
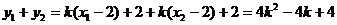
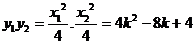 ,代入上式有:
,代入上式有:
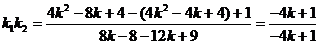
当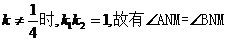
当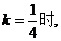 解得A,B两点的坐标分别为
解得A,B两点的坐标分别为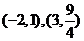 ,知直线AN与BN的斜率一个为零,另一个不存在,也有
,知直线AN与BN的斜率一个为零,另一个不存在,也有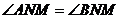 。综上所述,命题得证。
。综上所述,命题得证。
22.解:⑴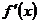
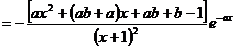
由已知有: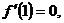 ∴a+(ab+a)+ab+b-1=0,∴
∴a+(ab+a)+ab+b-1=0,∴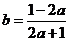
从而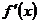
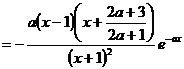
令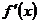 =0得:x1=1,x2=
=0得:x1=1,x2=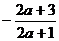 .
∵
.
∵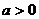 ∴x2
∴x2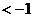
当x变化时,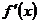 、f(x)的变化情况如下表:
、f(x)的变化情况如下表:
|
x |
 |
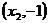 |
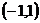 |
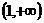 |
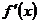 |
- |
+ |
+ |
- |
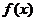 |
减函数 |
增函数 |
增函数 |
减函数 |
从上表可知: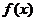 在
在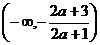 ,
,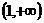 上是减函数;
上是减函数;
在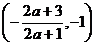 ,
,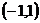 上是增函数.
上是增函数.
⑵ ∵m>-1,由(I)知:
① 当-1<m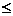 0时, m+1
0时, m+1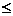 1,
1,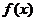 在闭区间
在闭区间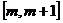 上是增函数.
上是增函数.
∴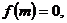 且
且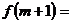
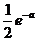 .
.
化简得: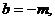
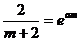 .
.
又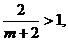
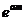 <1.故此时的a,m不存在.
<1.故此时的a,m不存在.
② 当m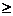 1时,
1时, 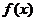 在闭区间
在闭区间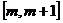 上是减函数.
上是减函数.
又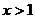 时
时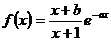 =
=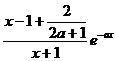
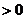 .其最小值不可能为0
.其最小值不可能为0
∴此时的a,m也不存在
⑴
当0<m<1时,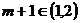 . 则最大值为
. 则最大值为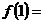
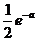 得:b=0,
得:b=0,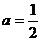
又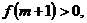
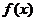 的最小值为
的最小值为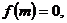 ∴
∴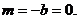
综上知: 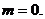
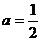 .
.