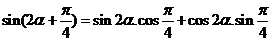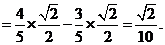1.设函数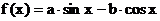 图象的一条对称轴方程为
图象的一条对称轴方程为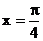 , 则直线
, 则直线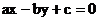 的倾斜角为
的倾斜角为
A. 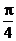 B.
B. 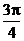 C.
C. 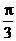 D.
D.
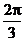
2.已知 ,那么
,那么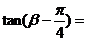 A.
A.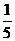 B.
B. 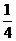 C.
C. 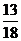 D.
D.

3.若函数f(x)同时具有以下两个性质:①f(x)是偶函数,②对任意实数x,都有f(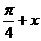 )= f(
)= f(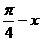 ),则f(x)的解析式可以是 A.f(x)=cosx B.f(x)=cos(2x
),则f(x)的解析式可以是 A.f(x)=cosx B.f(x)=cos(2x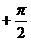 ) C.f(x)=sin(4x
) C.f(x)=sin(4x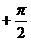 ) D.f(x) =cos6x
) D.f(x) =cos6x
4.把函数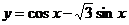 的图象沿向量
的图象沿向量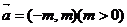 的方向平移后,所得的图象关于y轴对称,则m的最小值是
A.
的方向平移后,所得的图象关于y轴对称,则m的最小值是
A.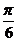 B.
B.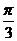 C.
C.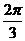 D.
D.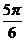
5.在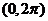 内,使
内,使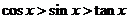 成立的
成立的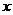 的取值范围是
的取值范围是
(A)(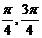 ) (B)(
) (B)(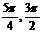 ) (C)(
) (C)(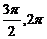 ) (D)(
) (D)(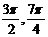 )
)
6.函数y=cosx(sinx+cosx)的最小正周期为 A 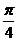 B
B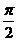 C
C 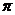 D
D 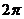
7.如果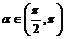 ,且
,且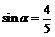 ,那么
,那么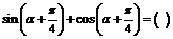 A.
A. 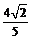 B.
B.
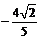 C.
C. 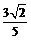 D.
D.
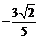
8.已知sin(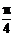 -x)=
-x)=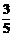 ,则sin2x的值为( )A.
,则sin2x的值为( )A. 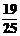 B.
B.
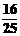 C.
C.
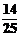 D.
D. 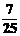
9.函数f(x)=sin(x+θ)+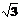 cos(x+θ)的图像关于点(5,0)对称,则θ的值是( )
cos(x+θ)的图像关于点(5,0)对称,则θ的值是( )
A.-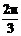 -10
B.-
-10
B.-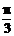 -5 C.2kπ-
-5 C.2kπ-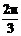 -10
D. kπ-
-10
D. kπ-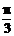 -5 (k∈Z)
-5 (k∈Z)
10.已知向量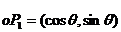 ,
,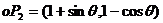 (O为原点,
(O为原点,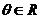 ),则向量
),则向量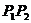 的长度的最大值是( )
的长度的最大值是( )
A.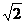 B.2
B.2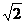 C.3
C.3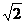 D.4
D.4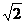
11.曲线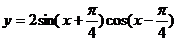 和直线
和直线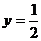 在
在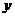 轴右侧的交点按横坐标从小到大依次记为P1,P2,P3,…,则
轴右侧的交点按横坐标从小到大依次记为P1,P2,P3,…,则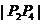 等于
A.
等于
A.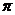 B.2
B.2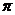 C.3
C.3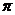 D.4
D.4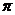
12.已知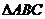 中,
中,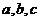 分别为角
分别为角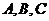 所对的边,且
所对的边,且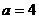 ,
,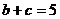 ,
,
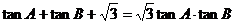 ,则
,则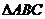 的面积为(A)
的面积为(A)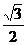 (B)
(B)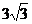 (C)
(C)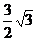 (D)
(D)
13.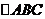 的三内角
的三内角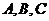 所对边的长分别为
所对边的长分别为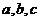 设向量
设向量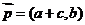 ,
,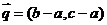 ,若
,若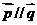 ,则角
,则角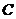 =
=
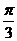
14.对于函数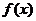 =
=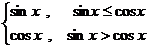 (
(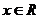 ), 则它的值域为 ;
), 则它的值域为 ;
15.已知sinα=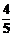 ,cos(α+β)=-
,cos(α+β)=-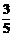 ,α、β∈(0,
,α、β∈(0,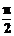 ),则sin2β的值为
。
),则sin2β的值为
。
16.定义运算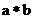 为:
为: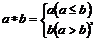 例如,
例如,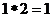 ,则函数
,则函数 的值域为 .
的值域为 .
1.已知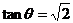 ,求(1)
,求(1)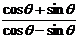 ;(2)
;(2)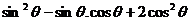 的值.
的值.
解:(1)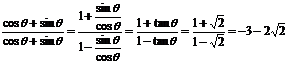 ;
;
(2) 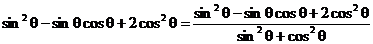
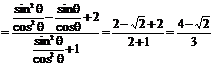 .
.
2.(上海卷)已知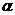 是第一象限的角,且
是第一象限的角,且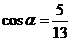 ,求
,求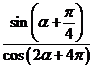 的值。
的值。
解: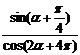 =
=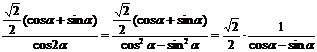
由已知可得sin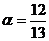 ,
∴原式=
,
∴原式=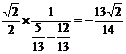 .
.
3.已知点A(2,0),B(0,2),C(cos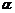 ,sin
,sin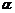 ),且0<
),且0<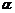 <
<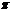 。
。
(1)若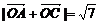 ,求
,求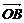 与
与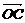 的夹角;(2)若
的夹角;(2)若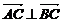 ,求tan
,求tan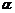 的值。
的值。
解:∵(1),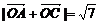
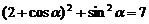 ∴
∴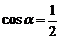
又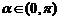 ,∴
,∴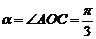 又
又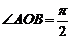 ,∴
,∴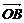 与
与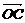 的夹角为
的夹角为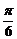 .
. (5分)
(5分)
(2) 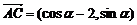 ,
,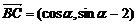 ∵
∵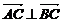 ,∴
,∴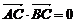
∴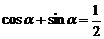 ∴
∴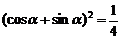 ∴
∴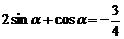 ∵
∵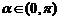 ∴
∴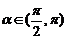
又由 及
及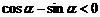 得
得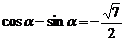
由①②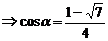 ,
,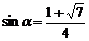 ∴
∴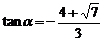 。
。
4.已知A (3,0),B (0,3),C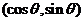 ①若
①若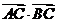 =-1,求
=-1,求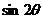 的值;
的值;
②若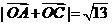 ,且
,且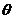 ∈(0,
∈(0,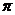 ),求
),求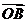 与
与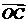 的夹角.
的夹角.
解答:(1)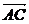 =(
=(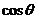 -3,
-3, ),
),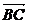 =(
=(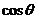 ,
, -3),∴由
-3),∴由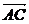 .
.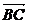 =-1,
=-1,
得(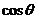 -3)
-3)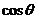 +
+ (
( -3)=-1,∴
-3)=-1,∴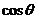 +
+ =
=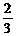 ,两边平方,得1+
,两边平方,得1+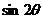 =
=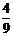 ,∴
,∴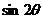 =-
=-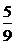
(2)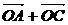 =(3+
=(3+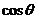 ,
, ),∴(3+
),∴(3+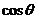 )2+
)2+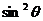 =13, ∴
=13, ∴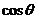 =
=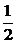 ,∵
,∵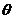 ∈(0,π),
∈(0,π),
∴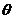 =
=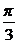
 =
=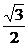 , ∴
, ∴ ,
,
设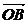 与
与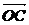 的夹角为
的夹角为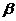 ,则
,则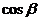 =
=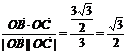 ,∴
,∴ 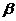 =
=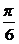 即为所求.
即为所求.
5.已知向量 ,
, .(Ⅰ)当
.(Ⅰ)当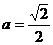 ,且
,且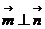 时,求
时,求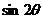 的值; (Ⅱ)当
的值; (Ⅱ)当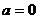 ,且
,且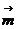 ∥
∥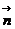 时,求
时,求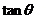 的值.
的值.
解:(Ⅰ)当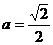 时,
时,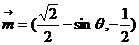 ,
,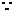
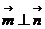 ,
,  由
由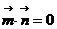 , 得
, 得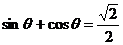 ,
,
上式两边平方得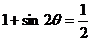 ,因此,
,因此,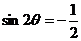 .
.
(Ⅱ)当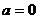 时,
时,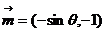 ,由
,由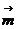 ∥
∥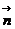 得
得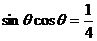 .
.
即 .
. 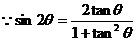 ,
,
 或
或  .
.
6.(安徽卷)已知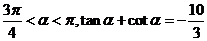 (Ⅰ)求
(Ⅰ)求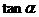 的值;
的值;
(Ⅱ)求 的值。
的值。
解:(Ⅰ)由 得
得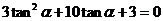 ,即
,即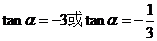 ,
,
又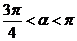 ,所以
,所以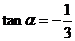 为所求。
为所求。
(Ⅱ)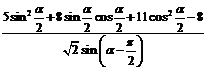 =
=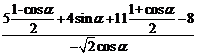
=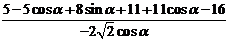 =
=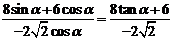 =
=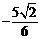 。
。
7.(北京卷)已知函数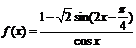 , (Ⅰ)求
, (Ⅰ)求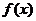 的定义域;
的定义域;
(Ⅱ)设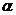 是第四象限的角,且
是第四象限的角,且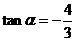 ,求
,求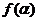 的值.
的值.
解:(1)依题意,有cosx¹0,解得x¹kp+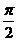 ,即
,即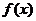 的定义域为{x|xÎR,且x¹kp+
的定义域为{x|xÎR,且x¹kp+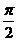 ,kÎZ}
,kÎZ}
(2)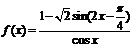 =-2sinx+2cosx\
=-2sinx+2cosx\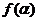 =-2sina+2cosa
=-2sina+2cosa
由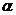 是第四象限的角,且
是第四象限的角,且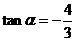 可得sina=-
可得sina=-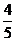 ,cosa=
,cosa=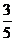 \
\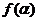 =-2sina+2cosa=
=-2sina+2cosa=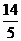
8. (天津卷)已知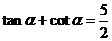 ,
,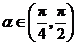 .求
.求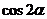 和
和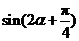 的值.
的值.
本小题考查同角三角函数关系、两角和公式、倍角公式等基础知识,考查基本运算能力。
解法一:由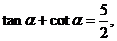 得
得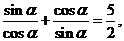 则
则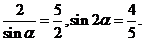
因为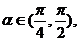 所以
所以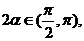
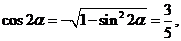
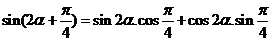
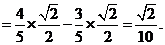
解法二:由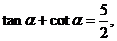 得
得 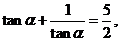
解得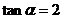 或
或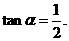 由已知
由已知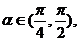 故舍去
故舍去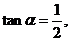 得
得 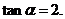
因此,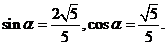 那么
那么 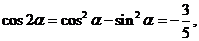
且
故