
1.已知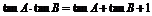 ,则
,则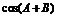 的值是 ( )
的值是 ( )
A.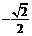 B.
B. 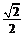 C.
C. 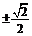 D.
D. 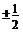
2.将函数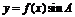 的图象向右平移
的图象向右平移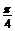 个单位后,再作关于
个单位后,再作关于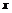 轴对称的曲线,得到函数
轴对称的曲线,得到函数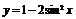 , 则
, 则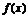 是
( )
是
( )
A.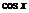 B.
B.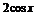 C.
C.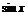 D.
D.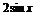
3.已知钝角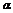 的终边经过点
的终边经过点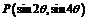 ,且
,且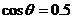 ,则
,则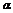 的值为 ( )
的值为 ( )
A. B.
B.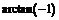 C.
C. D.
D.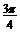
4.曲线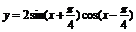 和直线
和直线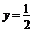 在y轴右侧的交点按横坐标从小到大依次记为
在y轴右侧的交点按横坐标从小到大依次记为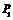 ,
,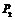 ,
,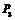 ,…,则
,…,则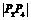 等于 ( )
等于 ( )
A.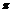 B.2
B.2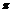 C.3
C.3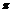 D.4
D.4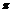
5.已知函数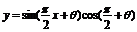 在
在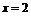 时最大值, 则θ的一个值是 ( )
时最大值, 则θ的一个值是 ( )
A.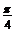 B.
B.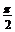 C.
C.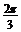 D.
D.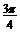
6.若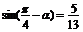 ,且
,且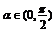 , 则
, 则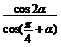 值为
( )
值为
( )
A.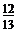 B.
B.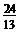 C.
C.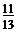 D.
D.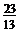
7.若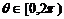 ,
,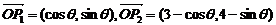 ,则
,则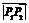 的取值范围是(
)
的取值范围是(
)
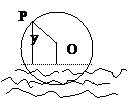 A.[4,7]
B.[3,7]
C.[3,5]
D.[5,6]
A.[4,7]
B.[3,7]
C.[3,5]
D.[5,6]
8.如图是半径为3米的水轮,水轮圆心O距离水面2米.已知水轮每分钟旋转4圈,水轮上一点P到水面的距离Y(米)与时间X(秒)满足函数关系式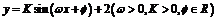 ,则有 ( )
,则有 ( )
A.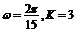 B.
B.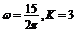 C.
C.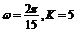 D.
D.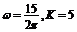
9.已知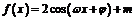 ,恒有
,恒有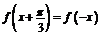 成立,且
成立,且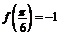 ,则实数
,则实数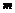 的值为(
)
的值为(
)
A.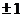 B.
B.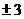 C.-1或3 D.-3或1
C.-1或3 D.-3或1
10.已知A是△ABC的一个内角,且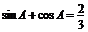 ,则△ABC是 (
)
,则△ABC是 (
)
A.锐角三角形 B.钝角三角形 C.直角三角形 D.形状不确定
11.函数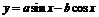 的一条对称轴方程为
的一条对称轴方程为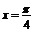 ,则直线
,则直线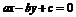 的倾斜角是(
)
的倾斜角是(
)
A.45° B.135° C.60° D.120°
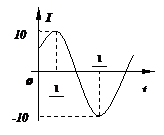
12.已知函数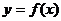 图象如图甲,则
图象如图甲,则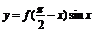 在区间[0,
在区间[0,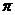 ]上大致图象是(
)
]上大致图象是(
)

 13.定义运算
13.定义运算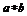 为:
为: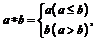 例如,
例如,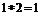 ,则函数
,则函数 的值域为 .
的值域为 .
14.电流强度I(安)随时间t(秒)变化的函数
I=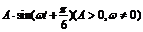 的图象如图
的图象如图
所示,则当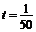 秒时,电流强度是
安.
秒时,电流强度是
安.
15. 最小值为__________.
最小值为__________.
16.已知点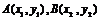 是函数
是函数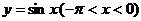 上的两个不同点,且
上的两个不同点,且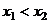 ,试根据图像特征判定下列四个不等式的正确性:①
,试根据图像特征判定下列四个不等式的正确性:①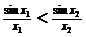 ;②
;②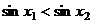 ;③
;③
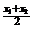 ;④
;④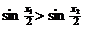 。其中正确不等式的序号是
.
。其中正确不等式的序号是
.
17.(本小题满分12分)已知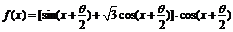 .
若
.
若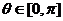 且f(x)为偶函数,求
且f(x)为偶函数,求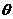 的值.
的值.
18.(本小题满分12分)已知: 为常数)
为常数)
(1)若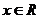 ,求
,求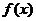 的最小正周期;
的最小正周期;
(2)若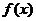 在
在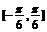 上最大值与最小值之和为3,求
上最大值与最小值之和为3,求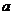 的值;
的值;
(3)在(2)条件下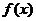 先按
先按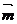 平移后再经过伸缩变换后得到
平移后再经过伸缩变换后得到 求
求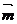 .
.
19.(本小题满分12分)已知定义在区间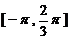 上的函数
上的函数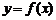 的图象关于直线
的图象关于直线

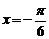 对称,当
对称,当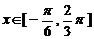 时,函数
时,函数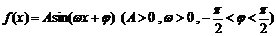 ,
,
其图象如图所示.
(1)求函数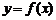 在
在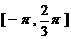 的表达式;
的表达式;
(2)求方程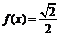 的解.
的解.
20.(本小题满分12分) 已知向量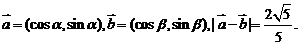
(1)求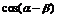 的值;
的值;
(2)若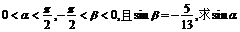 的值.
的值.
21.(本小题满分12分)已知函数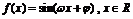 ,(其中
,(其中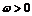 )的图象与x轴在原点右侧
)的图象与x轴在原点右侧
的第一个交点为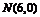 ,又
,又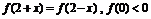 ,求这个函数的解析式.
,求这个函数的解析式.
22.(本小题满分14分)已知△ABC的周长为6, 成等比数列,求
成等比数列,求
(1)△ABC的面积S的最大值;
(2)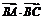 的取值范围.
的取值范围.
高考数学三角函数专项训练(03)参考答案
参 考 答 案(三)
一、选择题:(1).C (2).B (3).D (4).A (5).A (6).B (7).B (8).A (9).D (10).B (11). B (12). D
二、填空题:(13). [-1,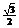 ] ; (14).5 ; (15).
] ; (14).5 ; (15). 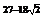 ; (16). ①③
; (16). ①③
三、解答题17.解: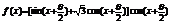
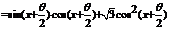
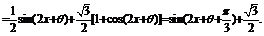 ……5分
……5分
∵f(x)为偶函数。∴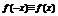 …………7分;即
…………7分;即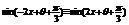 得
得 …………9分
…………9分
∴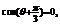 …………11分 又
…………11分 又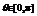 ∴
∴ .………12分
.………12分
18.解: ……2分 (1)最小正周期
……2分 (1)最小正周期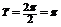 ……4分
……4分
(2)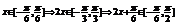
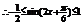 …6分即
…6分即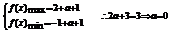 ……8分
……8分
(3)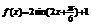
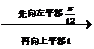
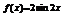 ……10分
……10分 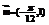 ……12分
……12分
19.解:(1)当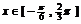 时,函数
时,函数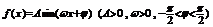 ,观察图象易得:
,观察图象易得: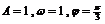 ,即时,函数
,即时,函数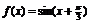 ,由函数
,由函数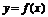 的图象关于直线
的图象关于直线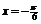 对称得,
对称得,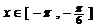 时,
时,
函数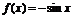 . ∴
. ∴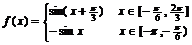 .
.
(2)当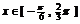 时,由
时,由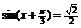 得,
得,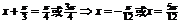 ;
;
当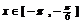 时,由
时,由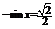 得,
得,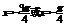 .∴方程
.∴方程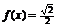 的解集为
的解集为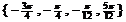
20. 解:(1)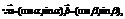
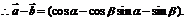 ……2分
……2分
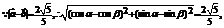 ……4分
……4分 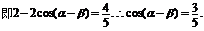 ……6分
……6分
(2)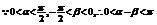 ……7分
……7分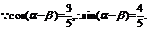 ……8分
……8分
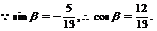 …9分
…9分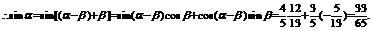 …12分
…12分
21. 解:
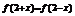 ∴
∴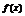 关于
关于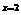 对称,又x轴在原点右侧的第一个交点为N(6,0)∴
对称,又x轴在原点右侧的第一个交点为N(6,0)∴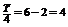 ,即
,即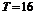
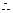
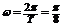 …4分 将
…4分 将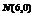 代入
代入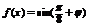 得:
得: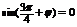 得:
得: 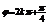 或
或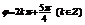 …8分
…8分
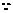
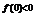 ∴
∴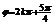 (kÎZ),满足条件的最小正数
(kÎZ),满足条件的最小正数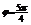 ……10分∴所求解析式
……10分∴所求解析式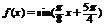 ……12分
……12分
22.解设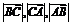 依次为
依次为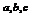 ,则
,则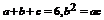 ,由余弦定理得
,由余弦定理得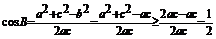
故有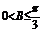 ,又
,又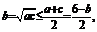 从而
从而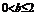 …6分
…6分
(1)所以 ,即
,即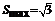 …8分
…8分
(2)所以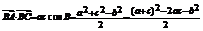
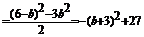 …12分
…12分
 ……14分
……14分