
1.在掌握等差数列、等比数列的定义、性质、通项公式、前n项和公式的基础上,系统掌握解等差数列与等比数列综合题的规律,深化数学思想方法在解题实践中的指导作用,灵活地运用数列知识和方法解决数学和实际生活中的有关问题;
3.培养学生善于分析题意,富于联想,以适应新的背景,新的设问方式,提高学生用函数的思想、方程的思想研究数列问题的自觉性、培养学生主动探索的精神和科学理性的思维方法.
1.判断和证明数列是等差(等比)数列常有三种方法:
(1)定义法:对于n≥2的任意自然数,验证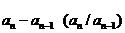 为同一常数。
为同一常数。
(2)通项公式法:
①若 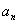 =
= 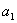 +(n-1)d=
+(n-1)d= 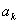 +(n-k)d ,则
+(n-k)d ,则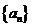 为等差数列;
为等差数列;
②若 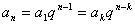 ,则
,则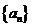 为等比数列。
为等比数列。
(3)中项公式法:验证中项公式成立。
2. 在等差数列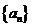 中,有关
中,有关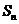 的最值问题--常用邻项变号法求解:
的最值问题--常用邻项变号法求解:
(1)当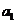 >0,d<0时,满足
>0,d<0时,满足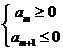 的项数m使得
的项数m使得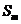 取最大值.
取最大值.
(2)当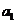 <0,d>0时,满足
<0,d>0时,满足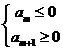 的项数m使得
的项数m使得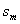 取最小值。
取最小值。
在解含绝对值的数列最值问题时,注意转化思想的应用。
3.数列求和的常用方法:公式法、裂项相消法、错位相减法、倒序相加法等。
1.证明数列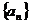 是等差或等比数列常用定义,即通过证明
是等差或等比数列常用定义,即通过证明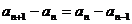 或
或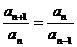 而得。
而得。
2.在解决等差数列或等比数列的相关问题时,“基本量法”是常用的方法,但有时灵活地运用性质,可使运算简便,而一般数列的问题常转化为等差、等比数列求解。
3.注意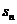 与
与 之间关系的转化。如:
之间关系的转化。如: =
=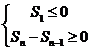
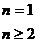 ,
,  =
=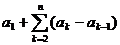 .
.
4.数列极限的综合题形式多样,解题思路灵活,但万变不离其宗,就是离不开数列极限的概念和性质,离不开数学思想方法,只要能把握这两方面,就会迅速打通解题思路.
5.解综合题的成败在于审清题目,弄懂来龙去脉,透过给定信息的表象,抓住问题的本质,揭示问题的内在联系和隐含条件,明确解题方向,形成解题策略.
[问题1]等差、等比数列的项与和特征问题P49 例1 3。P50 例2 P56 例1 P59 T6.
[注1]文中所列例题如末给题目原文均为广州市二轮复习资料上例题
例(四川卷)数列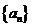 的前
的前 项和记为
项和记为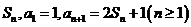 (Ⅰ)求
(Ⅰ)求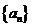 的通项公式;(Ⅱ)等差数列
的通项公式;(Ⅱ)等差数列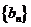 的各项为正,其前
的各项为正,其前 项和为
项和为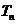 ,且
,且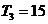 ,又
,又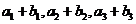 成等比数列,求
成等比数列,求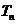
本小题主要考察等差数列、等比数列的基础知识,以及推理能力与运算能力。满分12分。
解:(Ⅰ)由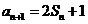 可得
可得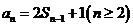 ,两式相减得
,两式相减得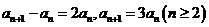
又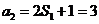 ∴
∴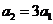 故
故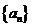 是首项为
是首项为 ,公比为
,公比为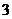 得等比数列 ∴
得等比数列 ∴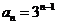
(Ⅱ)设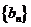 的公比为
的公比为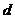 由
由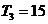 得,可得
得,可得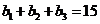 ,可得
,可得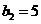
故可设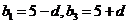 又
又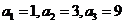
由题意可得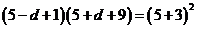 解得
解得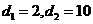
∵等差数列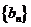 的各项为正,∴
的各项为正,∴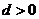 ∴
∴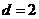 ∴
∴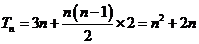
1.设等差数列{an}的首项a1及公差d都为整数,前n项和为Sn.
(Ⅰ)若a11=0,S14=98,求数列{an}的通项公式;
(Ⅱ)若a1≥6,a11>0,S14≤77,求所有可能的数列{an}的通项公式
2.(上海卷)设数列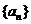 的前
的前 项和为
项和为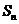 ,且对任意正整数
,且对任意正整数 ,
,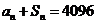 。(1)求数列
。(1)求数列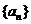 的通项公式?(2)设数列
的通项公式?(2)设数列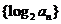 的前
的前 项和为
项和为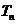 ,对数列
,对数列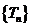 ,从第几项起
,从第几项起 ?
?
.解(1) ∵an+ Sn=4096, ∴a1+ S1=4096, a1 =2048.
当n≥2时, an= Sn-Sn-1=(4096-an)-(4096-an-1)= an-1-an
∴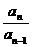 =
=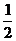 an=2048(
an=2048(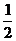 )n-1.
)n-1.
(2) ∵log2an=log2[2048(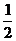 )n-1]=12-n,
∴Tn=
)n-1]=12-n,
∴Tn=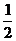 (-n2+23n).
(-n2+23n).
由Tn<-509,解得n>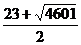 ,而n是正整数,于是,n≥46.
∴从第46项起Tn<-509.
,而n是正整数,于是,n≥46.
∴从第46项起Tn<-509.
3. (全国卷Ⅰ) 设正项等比数列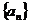 的首项
的首项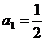 ,前n项和为
,前n项和为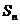 ,且
,且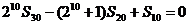 。(Ⅰ)求
。(Ⅰ)求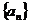 的通项;(Ⅱ)求
的通项;(Ⅱ)求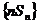 的前n项和
的前n项和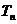 。
。
解:(Ⅰ)由 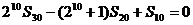 得
得 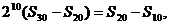
即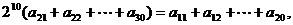
可得
因为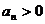 ,所以
,所以 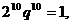 解得
解得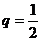 ,因而
,因而 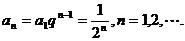
(Ⅱ)因为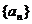 是首项
是首项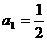 、公比
、公比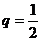 的等比数列,故
的等比数列,故
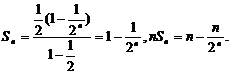
则数列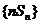 的前n项和
的前n项和
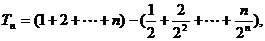
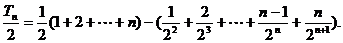
前两式相减,得 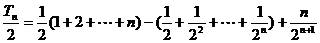
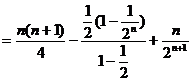 即
即 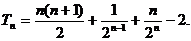
[问题2]等差、等比数列的判定问题.P53 T7 例P54 T9
[例]P54 T9(上海卷)已知有穷数列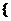

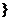 共有2
共有2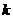 项(整数
项(整数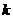 ≥2),首项
≥2),首项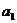 =2.设该数列的前
=2.设该数列的前 项和为
项和为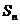 ,且
,且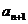 =
=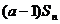 +2(
+2( =1,2,┅,2
=1,2,┅,2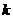 -1),其中常数
-1),其中常数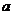 >1.
>1.
(1)求证:数列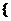

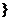 是等比数列;(2)若
是等比数列;(2)若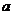 =2
=2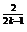 ,数列
,数列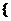
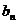
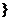 满足
满足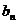 =
=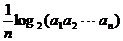 (
( =1,2,┅,2
=1,2,┅,2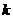 ),求数列
),求数列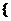
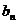
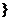 的通项公式;
的通项公式;
(3)若(2)中的数列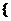
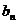
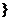 满足不等式|
满足不等式| -
- |+|
|+|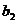 -
- |+┅+|
|+┅+|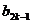 -
- |+|
|+|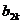 -
- |≤4,求
|≤4,求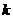 的值.
的值.
(1) [证明] 当n=1时,a2=2a,则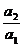 =a;
=a;
2≤n≤2k-1时, an+1=(a-1) Sn+2, an=(a-1) Sn-1+2,
an+1-an=(a-1) an, ∴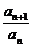 =a, ∴数列{an}是等比数列.
=a, ∴数列{an}是等比数列.
(2) 解:由(1)
得an=2a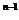 , ∴a1a2…an=2
, ∴a1a2…an=2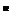 a
a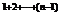 =2
=2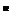 a
a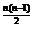 =2
=2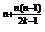 ,
,
bn= (n=1,2,…,2k).
(n=1,2,…,2k).
(3)设bn≤ ,解得n≤k+
,解得n≤k+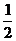 ,又n是正整数,于是当n≤k时, bn<
,又n是正整数,于是当n≤k时, bn< ;
;
当n≥k+1时, bn> .
.
原式=( -b1)+(
-b1)+( -b2)+…+(
-b2)+…+( -bk)+(bk+1-
-bk)+(bk+1- )+…+(b2k-
)+…+(b2k- )
)
=(bk+1+…+b2k)-(b1+…+bk)
=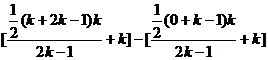 =
=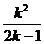 .
.
当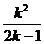 ≤4,得k2-8k+4≤0, 4-2
≤4,得k2-8k+4≤0, 4-2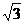 ≤k≤4+2
≤k≤4+2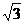 ,又k≥2,
,又k≥2,
∴当k=2,3,4,5,6,7时,原不等式成立.
4.[例],已知数列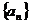 中,
中,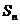 是其前
是其前 项和,并且
项和,并且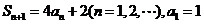 ,⑴设数列
,⑴设数列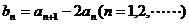 ,求证:数列
,求证:数列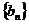 是等比数列;⑵设数列
是等比数列;⑵设数列 ,求证:数列
,求证:数列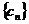 是等差数列;⑶求数列
是等差数列;⑶求数列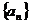 的通项公式及前
的通项公式及前 项和。
项和。
分析:由于{b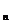 }和{c
}和{c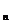 }中的项都和{a
}中的项都和{a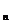 }中的项有关,{a
}中的项有关,{a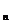 }中又有S
}中又有S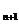 =4a
=4a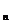 +2,可由S
+2,可由S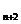 -S
-S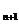 作切入点探索解题的途径.
作切入点探索解题的途径.
[注2]本题立意与2007年高考题文科20题结构相似.
解:(1)由S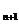 =4a
=4a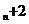 ,S
,S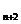 =4a
=4a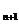 +2,两式相减,得S
+2,两式相减,得S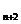 -S
-S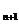 =4(a
=4(a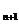 -a
-a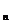 ),即a
),即a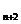 =4a
=4a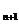 -4a
-4a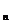 .(根据b
.(根据b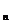 的构造,如何把该式表示成b
的构造,如何把该式表示成b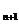 与b
与b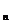 的关系是证明的关键,注意加强恒等变形能力的训练)
的关系是证明的关键,注意加强恒等变形能力的训练)
a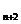 -2a
-2a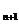 =2(a
=2(a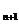 -2a
-2a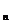 ),又b
),又b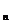 =a
=a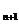 -2a
-2a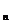 ,所以b
,所以b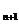 =2b
=2b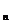 ①
①
已知S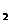 =4a
=4a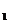 +2,a
+2,a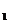 =1,a
=1,a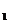 +a
+a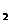 =4a
=4a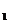 +2,解得a
+2,解得a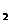 =5,b
=5,b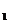 =a
=a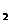 -2a
-2a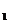 =3 ②
=3 ②
由①和②得,数列{b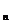 }是首项为3,公比为2的等比数列,故b
}是首项为3,公比为2的等比数列,故b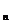 =3.2
=3.2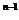 .
.
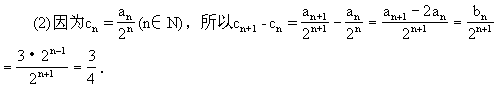

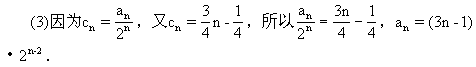
当n≥2时,S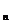 =4a
=4a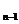 +2=2
+2=2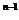 (3n-4)+2;当n=1时,S
(3n-4)+2;当n=1时,S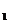 =a
=a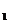 =1也适合上式.
=1也适合上式.
综上可知,所求的求和公式为S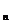 =2
=2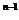 (3n-4)+2.
(3n-4)+2.
说明:1.本例主要复习用等差、等比数列的定义证明一个数列为等差,等比数列,求数列通项与前 项和。解决本题的关键在于由条件
项和。解决本题的关键在于由条件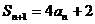 得出递推公式。
得出递推公式。
2.解综合题要总揽全局,尤其要注意上一问的结论可作为下面论证的已知条件,在后面求解的过程中适时应用.
[问题3]函数与数列的综合题 P51 例3
数列是一特殊的函数,其定义域为正整数集,且是自变量从小到大变化时函数值的序列。注意深刻理解函数性质对数列的影响,分析题目特征,探寻解题切入点.
P51 例3已知二次函数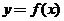 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为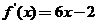 ,数列
,数列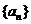 的前n项和为
的前n项和为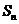 ,点
,点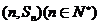 均在函数
均在函数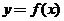 的图像上。(Ⅰ)、求数列
的图像上。(Ⅰ)、求数列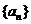 的通项公式;(Ⅱ)、设
的通项公式;(Ⅱ)、设 ,
,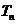 是数列
是数列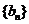 的前n项和,求使得
的前n项和,求使得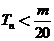 对所有
对所有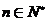 都成立的最小正整数m;
都成立的最小正整数m;
点评:本题考查二次函数、等差数列、数列求和、不等式等基础知识和基本的运算技能,考查分析问题的能力和推理能力。
解:(Ⅰ)设这二次函数f(x)=ax2+bx (a≠0) ,则 f`(x)=2ax+b,由于f`(x)=6x-2,得
a=3 , b=-2, 所以 f(x)=3x2-2x.
又因为点 均在函数
均在函数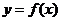 的图像上,所以
的图像上,所以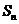 =3n2-2n.
=3n2-2n.
当n≥2时,an=Sn-Sn-1=(3n2-2n)-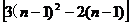 =6n-5.
=6n-5.
当n=1时,a1=S1=3×12-2=6×1-5,所以,an=6n-5 ( )
)
(Ⅱ)由(Ⅰ)得知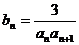 =
=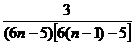 =
=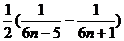 ,
,
故Tn=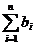 =
=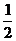
 =
=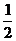 (1-
(1-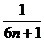 ).
).
因此,要使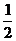 (1-
(1-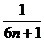 )<
)<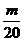 (
( )成立的m,必须且仅须满足
)成立的m,必须且仅须满足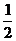 ≤
≤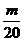 ,即m≥10,所以满足要求的最小正整数m为10.
,即m≥10,所以满足要求的最小正整数m为10.
5.设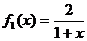 ,定义
,定义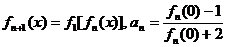 ,其中n∈N*.
,其中n∈N*.
(1)求数列{an}的通项公式;(2)若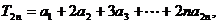 ,
,
解:(1)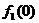 =2,
=2,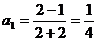 ,
, ,
,
∴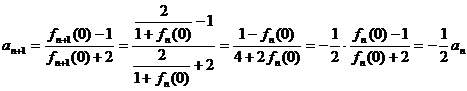
∴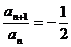 ,∴数列{an}上首项为
,∴数列{an}上首项为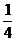 ,公比为
,公比为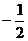 的等比数列,
的等比数列,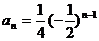
(2)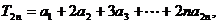
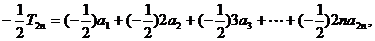
两式相减得:

6.(湖北卷)设数列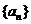 的前n项和为
的前n项和为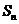 ,点
,点 均在函数y=3x-2的图像上。
均在函数y=3x-2的图像上。
(Ⅰ)求数列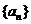 的通项公式;(Ⅱ)设
的通项公式;(Ⅱ)设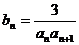 ,
,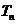 是数列
是数列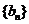 的前n项和,求使得
的前n项和,求使得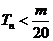 对所有
对所有 都成立的最小正整数m。
都成立的最小正整数m。
本小题主要是考查等差数列、数列求和、不等式等基础知识和基本的运算技能,考查分析问题能力和推理能力。
解:(I)依题意得,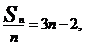 即
即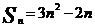 。
。
当n≥2时,a ;
;
当n=1时,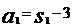 ×
×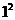 -2×1-1-6×1-5
-2×1-1-6×1-5
所以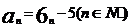 。
。
(II)由(I)得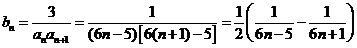 ,
,
故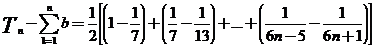 =
= 。
。
因此,使得 ﹤
﹤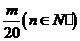 成立的m必须满足
成立的m必须满足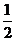 ≤
≤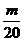 ,即m≥10,故满足要求的最小整数m为10。
,即m≥10,故满足要求的最小整数m为10。
[问题4]数列与解析几何
数列与解析几何综合题,是今后高考命题的重点内容之一,求解时要充分利用数列、解析几何的概念、性质,并结合图形求解.
例3.在直角坐标平面上有一点列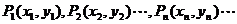 ,对一切正整数
,对一切正整数 ,点
,点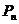 位于函数
位于函数 的图象上,且
的图象上,且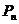 的横坐标构成以
的横坐标构成以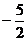 为首项,
为首项,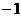 为公差的等差数列
为公差的等差数列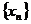 .
.
⑴求点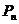 的坐标;子⑵设抛物线列
的坐标;子⑵设抛物线列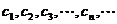 中的每一条的对称轴都垂直于
中的每一条的对称轴都垂直于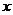 轴,第
轴,第 条抛物线
条抛物线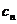 的顶点为
的顶点为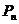 ,且过点
,且过点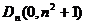 ,记与抛物线
,记与抛物线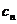 相切于
相切于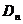 的直线的斜率为
的直线的斜率为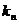 ,求:
,求: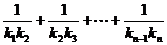 .
.
解:(1)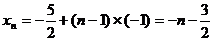
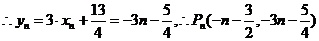
(2)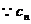 的对称轴垂直于
的对称轴垂直于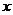 轴,且顶点为
轴,且顶点为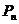 .
.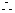 设
设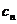 的方程为:
的方程为: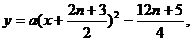
把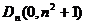 代入上式,得
代入上式,得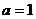 ,
,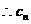 的方程为:
的方程为: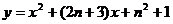 。
。
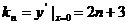 ,
,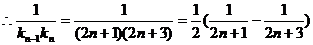
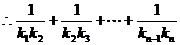

=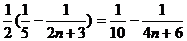
点评:本例为数列与解析几何的综合题,难度较大。(1)、(2)两问运用几何知识算出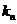 .
.
7.已知抛物线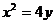 ,过原点作斜率1的直线交抛物线于第一象限内一点
,过原点作斜率1的直线交抛物线于第一象限内一点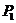 ,又过点
,又过点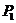 作斜率为
作斜率为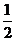 的直线交抛物线于点
的直线交抛物线于点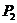 ,再过
,再过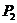 作斜率为
作斜率为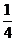 的直线交抛物线于点
的直线交抛物线于点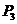 ,
,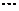 ,如此继续,一般地,过点
,如此继续,一般地,过点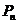 作斜率为
作斜率为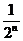 的直线交抛物线于点
的直线交抛物线于点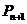 ,设点
,设点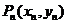 .
.
(Ⅰ)令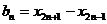 ,求证:数列
,求证:数列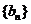 是等比数列.并求数列
是等比数列.并求数列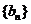 的前
的前 项和为
项和为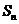
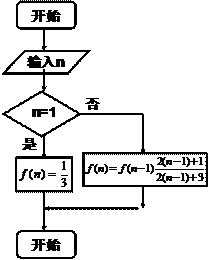 解:(1)因为
解:(1)因为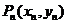 、
、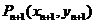 在抛物线上,故
在抛物线上,故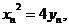 ①
①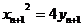 ②,又因为直线
②,又因为直线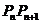 的斜率为
的斜率为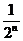 ,即
,即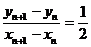 ,①②代入可得
,①②代入可得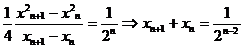
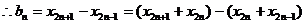
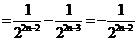 , 故
, 故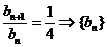 是以
是以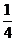
为公比的等比数列;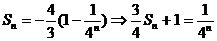 ,
,
[问题5]数列与算法
8. 数列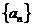 的前
的前 项和为
项和为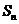 =n2+2n-1,试用程序框图
=n2+2n-1,试用程序框图
表示数列通项 的过程,并写出数列的前5项和通项公式
的过程,并写出数列的前5项和通项公式 .
.
9.根据流程图,(1)求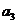 ;(2)若
;(2)若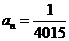 ,求n.
,求n.
[问题6]数列创新题
10.(安徽卷)数列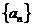 的前
的前 项和为
项和为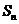 ,已知
,已知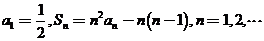
(Ⅰ)写出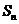 与
与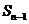 的递推关系式
的递推关系式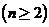 ,并求
,并求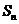 关于
关于 的表达式;
的表达式;
(Ⅱ)设 ,求数列
,求数列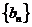 的前
的前 项和
项和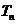 。
。
解:由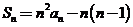
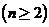 得:
得: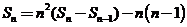 ,即
,即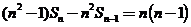 ,所以
,所以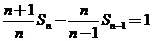 ,对
,对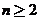 成立。
成立。
由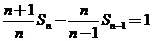 ,
,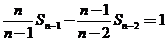 ,…,
,…,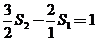 相加得:
相加得: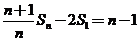 ,又
,又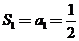 ,所以
,所以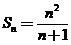 ,当
,当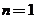 时,也成立。
时,也成立。
(Ⅱ)由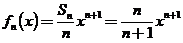 ,得
,得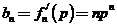 。
。
而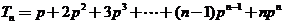 ,
,
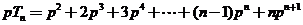 ,
,
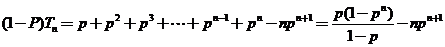
11.(福建卷)已知数列{an}满足a1=a,
an+1=1+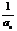 我们知道当a取不同的值时,得到不同的数列,如当a=1时,得到无穷数列:
我们知道当a取不同的值时,得到不同的数列,如当a=1时,得到无穷数列: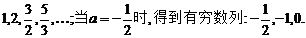
(Ⅰ)求当a为何值时a4=0;(Ⅱ)设数列{bn}满足b1=-1,
bn+1=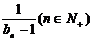 ,求证a取数列{bn}中的任一个数,都可以得到一个有穷数列{an};
,求证a取数列{bn}中的任一个数,都可以得到一个有穷数列{an};
(I)解法一: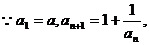
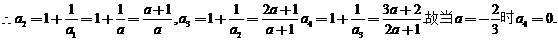
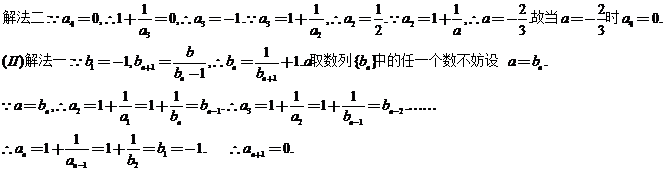 故a取数列{bn}中的任一个数,都可以得到一个有穷数列{an}
故a取数列{bn}中的任一个数,都可以得到一个有穷数列{an}
12. (全国卷III) 在等差数列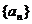 中,公差
中,公差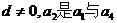 的等比中项.
的等比中项.
已知数列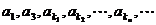 成等比数列,求数列
成等比数列,求数列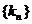 的通项
的通项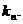
解:由题意得: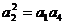 ……………1分
……………1分
即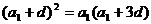 …………3分
…………3分
又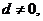
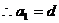 …………4分
…………4分
又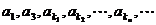 成等比数列,
成等比数列,
∴该数列的公比为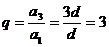 ,………6分
,………6分
所以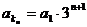 ………8分
………8分
又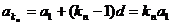 ……………………………………10分
……………………………………10分
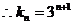 所以数列
所以数列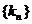 的通项为
的通项为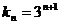 ……………………………12分
……………………………12分
课后训练:
1.如果-1,a, b,c,-9成等比数列,那么
A.b=3,ac=9 B.b=-3,ac=9 C.b=3,ac=-9 D.b=-3,ac=-9
2.在等差数列{a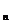 }中,已知a
}中,已知a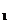 =2,a
=2,a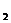 +a
+a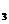 =13,则a
=13,则a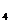 +a
+a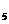 +a
+a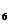 等于
等于
A.40 B.42 C.43 D.45
3.(06广东卷)已知某等差数列共有10项,其奇数项之和为15,偶数项之和为30,则其公差为
A.5 B.4 C. 3 D. 2
4.若互不相等的实数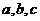 成等差数列,
成等差数列,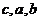 成等比数列,且
成等比数列,且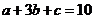 ,则
,则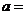
A.4 B.2 C.-2 D.-4
5.(06江西卷)已知等差数列{an}的前n项和为Sn,若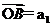
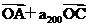 ,且A、B、C三点共线(该直线不过原点O),则S200=( )
,且A、B、C三点共线(该直线不过原点O),则S200=( )
A.100 B. 101 C.200 D.201
6.(文科做)在等比数列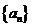 中,
中,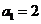 ,前
,前 项和为
项和为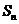 ,若数列
,若数列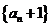 也是等比数列,则
也是等比数列,则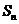 等于
等于
A.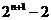 B.
B. 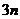 C.
C.
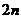 D.
D.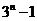
7.已知数列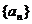 满足
满足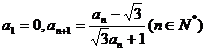 ,则
,则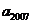 = ( )
= ( )
A.0 B.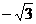 C.
C.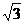 D.
D.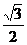
8.设Sn是等差数列{an}的前n项和,若=,则=
A. B. C. D.
9.已知等差数列{an}中,a2+a8=8,则该数列前9项和S9等于( )
A.18 B.27 C.36 D.45
10.已知数列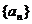 、
、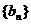 都是公差为1的等差数列,其首项分别为
都是公差为1的等差数列,其首项分别为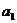 、
、 ,且
,且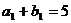 ,
,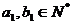 .设
.设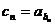 (
(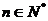 ),则数列
),则数列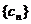 的前10项和等于( )
的前10项和等于( )
A.55 B.70 C.85 D.100
11.设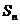 为等差数列
为等差数列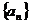 的前n项和,
的前n项和,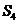 =14,S10-
=14,S10-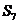 =30,则S9= .
=30,则S9= .
12.在数列{an}中,若a1=1,an+1=2an+3 (n≥1),则该数列的通项an=_________.
13. 已知a,b,a+b成等差数列,a,b,ab成等比数列,且0<logm(ab)<1,则m的取值范围是________
_
14. 等差数列{an}共有2n+1项,其中奇数项之和为319,偶数项之和为290,则其中间项为_________
15.设等比数列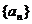 的公比为q,前n项和为Sn,若Sn+1,Sn,Sn+2成等差数列,则q的值为
.
的公比为q,前n项和为Sn,若Sn+1,Sn,Sn+2成等差数列,则q的值为
.
16 已知正项数列
已知正项数列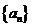 ,其前
,其前 项和
项和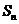 满足
满足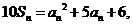 且
且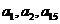 成等比数列,求数列
成等比数列,求数列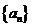 的通项
的通项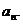
17.(文科做)(06福建)已知数列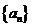 满足
满足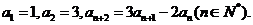
(I)证明:数列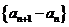 是等比数列; (II)求数列
是等比数列; (II)求数列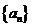 的通项公式;
的通项公式;
(II)若数列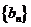 满足
满足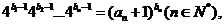 证明
证明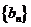 是等差数
是等差数
18.(山东卷)已知数列{ }中,
}中,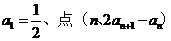 在直线y=x上,其中n=1,2,3….
在直线y=x上,其中n=1,2,3….
(Ⅰ)令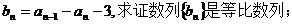 (Ⅱ)求数列
(Ⅱ)求数列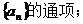
(Ⅲ)设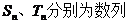
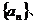
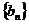 的前n项和,是否存在实数
的前n项和,是否存在实数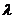 ,使得数列
,使得数列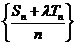 为等差数列?若存在,试求出
为等差数列?若存在,试求出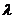 .若不存在,则说明理由。
.若不存在,则说明理由。
答案与点拨:
1 B 解:由等比数列的性质可得ac=(-1)×(-9)=9,b×b=9且b与奇数项的符号相同,故b=-3,选B
2 B解:在等差数列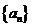 中,已知
中,已知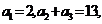 ∴
d=3,a5=14,
∴
d=3,a5=14,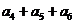 =3a5=42,选B.
=3a5=42,选B.
3 D解: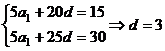 ,故选C.
,故选C.
4 D解:由互不相等的实数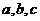 成等差数列可设a=b-d,c=b+d,由
成等差数列可设a=b-d,c=b+d,由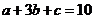 可得b=2,所以a=2-d,c=2+d,又
可得b=2,所以a=2-d,c=2+d,又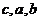 成等比数列可得d=6,所以a=-4,选D
成等比数列可得d=6,所以a=-4,选D
5 A解:依题意,a1+a200=1,故选A
6 (文)C 解:因数列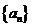 为等比,则
为等比,则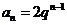 ,因数列
,因数列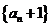 也是等比数列,
也是等比数列,
则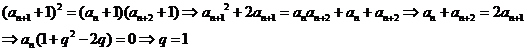
即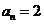 ,所以
,所以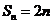 ,故选择答案C。
,故选择答案C。
7.A 提示:由a1=0,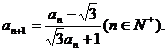 得a2=-
得a2=-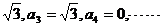
由此可知:数列{an}是周期变化的,且三个一循环,所以可得:a20=a2=-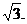 故选A
故选A
8 A 解:由等差数列的求和公式可得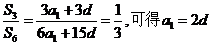 且
且
所以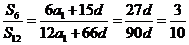 ,故选A
,故选A
点评:本题主要考察等比数列的求和公式,难度一般
9 C 解:在等差数列{an}中,a2+a8=8,∴  ,则该数列前9项和S9=
,则该数列前9项和S9=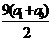 =36,选C
=36,选C
10 C 解:数列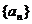 、
、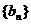 都是公差为1的等差数列,其首项分别为
都是公差为1的等差数列,其首项分别为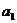 、
、 ,且
,且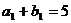 ,
,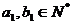 .设
.设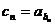 (
(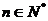 ),则数列
),则数列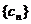 的前10项和等于
的前10项和等于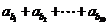 =
=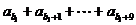 ,
,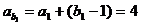 ,∴
,∴ 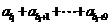
=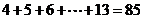 ,选C.
,选C.
11.(文)解:设等差数列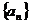 的首项为a1,公差为d,由题意得
的首项为a1,公差为d,由题意得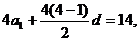
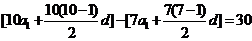 ,联立解得a1=2,d=1,所以S9=
,联立解得a1=2,d=1,所以S9=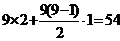
12. 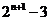 解:在数列
解:在数列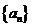 中,若
中,若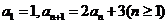 ,∴
,∴ 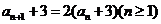 ,即{
,即{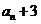 }是以
}是以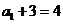 为首项,2为公比的等比数列,
为首项,2为公比的等比数列,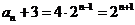 ,所以该数列的通项
,所以该数列的通项
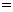
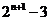 .
.
13 (-∞,8) 提示
(-∞,8) 提示 解出a、b,解对数不等式即可
解出a、b,解对数不等式即可 答案
答案 (-∞,8)
(-∞,8)
14 a11=29 提示
a11=29 提示 利用S奇/S偶=
利用S奇/S偶=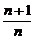 得解
得解 答案
答案 第11项a11=29
第11项a11=29
15.-2 提示:由题意可知q≠1,∴可得2(1-qn)=(1-qn+1)+(1-qn+2),即q2+q-2=0,解得q=-2或q=1(不合题意,舍去),∴q=-2.
16 解:13 解
解 ∵10Sn=an2+5an+6,
① ∴10a1=a12+5a1+6,解之得a1=2或a1=3.
∵10Sn=an2+5an+6,
① ∴10a1=a12+5a1+6,解之得a1=2或a1=3.
又10Sn-1=an-12+5an-1+6(n≥2),②
由①-②得 10an=(an2-an-12)+6(an-an-1),即(an+an-1)(an-an-1-5)=0
∵an+an-1>0 , ∴an-an-1=5 (n≥2).
当a1=3时,a3=13,a15=73. a1, a3,a15不成等比数列∴a1≠3;
当a1=2时, a3=12, a15=72, 有 a32=a1a15 , ∴a1=2, ∴an=5n-3.
17.(I)证明: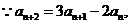
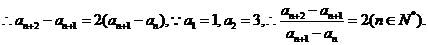
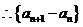 是以
是以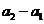
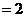 为首项,2为公比的等比数列。
为首项,2为公比的等比数列。
(II)解:由(I)得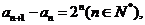
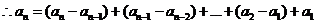
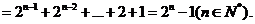
(III)证明: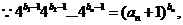
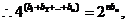
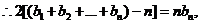 ①
①
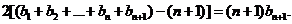 ②
②
②-①,得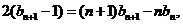 即
即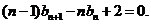 ③
③
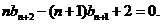 ④
④
④-③,得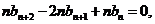 即
即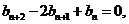
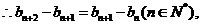
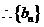 是等差数列。
是等差数列。
18.(山东卷)已知数列{ }中,
}中,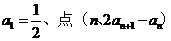 在直线y=x上,其中n=1,2,3….
在直线y=x上,其中n=1,2,3….
(Ⅰ)令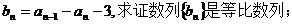 (Ⅱ)求数列
(Ⅱ)求数列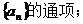
(Ⅲ)设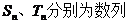
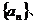
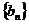 的前n项和,是否存在实数
的前n项和,是否存在实数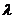 ,使得数列
,使得数列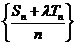 为等差数列?若存在,试求出
为等差数列?若存在,试求出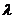 .若不存在,则说明理由。
.若不存在,则说明理由。
解:(I)由已知得 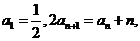

又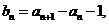
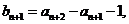
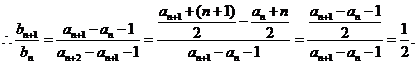
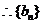 是以
是以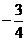 为首项,以
为首项,以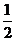 为公比的等比数列.
为公比的等比数列.
(II)由(I)知,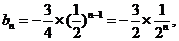
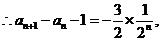
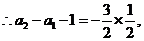
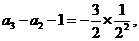
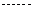
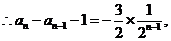
将以上各式相加得:

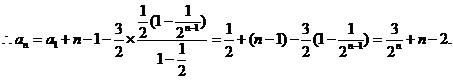
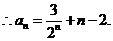
(III)解法一:
存在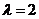 ,使数列
,使数列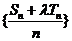 是等差数列.
是等差数列.
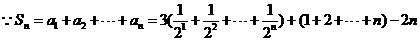

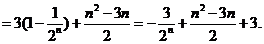

数列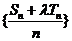 是等差数列的充要条件是
是等差数列的充要条件是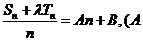 、
、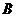 是常数
是常数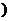
即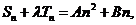
又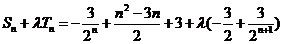
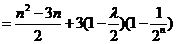
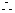 当且仅当
当且仅当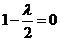 ,即
,即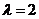 时,数列
时,数列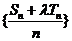 为等差数列.
为等差数列.
解法二:
存在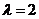 ,使数列
,使数列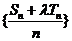 是等差数列.
是等差数列.
由(I)、(II)知,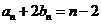
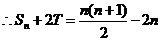

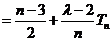
又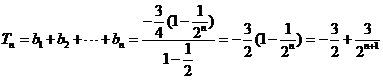
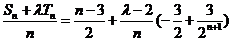
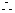 当且仅当
当且仅当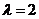 时,数列
时,数列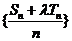 是等差数列.
是等差数列.