
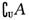 1.已知全集
1.已知全集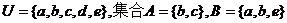 ,则( )∩B= ( )
,则( )∩B= ( )
A.{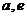 } B.
} B. C.
C. D.
D.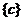
2.过点P(-2,4)作圆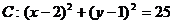 的切线l,直线
的切线l,直线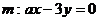 与直线l平行,则a的值是 ( )
与直线l平行,则a的值是 ( )
A.2 B.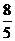 C.
C.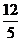 D.4
D.4
3.若关于x的不等式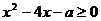 ,对任意
,对任意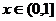 恒成立,则a的取值范围是( )
恒成立,则a的取值范围是( )
A.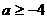 B.
B.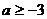 C.
C.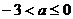 D.
D.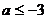
4.已知向量a=(λ,-2),b=(-3,5),且a与b的夹角为钝角,则λ的取值范围是( )
A.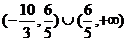 B.
B.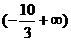
|
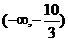 D.
D.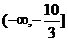
 5.如图,都不是正四面体的表面展开图的是 ( )
5.如图,都不是正四面体的表面展开图的是 ( )
A.①⑥ B.④⑤ C.②③ D.④⑥
6.已知a>b>c>0,t是方程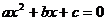 的实根,则t的取值范围是 ( )
的实根,则t的取值范围是 ( )
A.(-∞,-1) B.(-1,0) C.(0,1) D.(1,+∞)
7.正方体的八个顶点中,有四个顶点恰好是正四面体的顶点,则这个正方体的表面积与正四面体的表面积之比是 ( )
A. B.
B.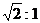 C.
C.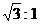 D.
D.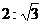
8.要得到函数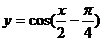 的图象,只需将y=sin
的图象,只需将y=sin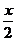 的图象 ( )
的图象 ( )
A.向左平移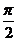 B.向右平移
B.向右平移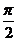 C.向左平移
C.向左平移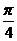 D.向右平移
D.向右平移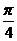
9.已知点P在曲线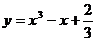 上移动,若经过点P的曲线的切线的倾斜角为α,则a的取值范围是 ( )
上移动,若经过点P的曲线的切线的倾斜角为α,则a的取值范围是 ( )
A.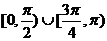 B.
B.
C.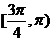 D.
D.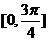
10.数列1,(1+2),(1+2+22),…,(1+2+…+2n-1),…的前n项和等于 ( )
A.2n B.2n -n C.2n+1 -n-2 D.n.2n
11.(理科答)甲、乙两名篮球队员轮流投篮至某人投中为止。设每次投篮甲投中的概率为0.4,乙投中的概率为0.6,而且不受其他投篮结果的影响。设甲投篮次数为ξ,且甲先投,则P(ξ=k)= ( )
A.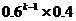 B.
B.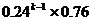 C.
C.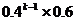 D.
D.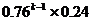
(文科答)要从10名女生与5名男生中选出6名学生组成课外学习小组,如果按性别分层随机抽样,则组成此课外学习小组的概率为 ( )
A.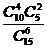 B.
B.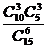 C.
C.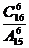 D.
D.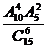
12.已知P是以F1、F2为焦点的双曲线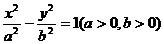 上的一点,若
上的一点,若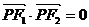 ,tan
,tan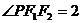 ,则此双曲线的离心率为 ( )
,则此双曲线的离心率为 ( )
A. B.3 C.5 D.
B.3 C.5 D.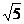
第II卷(非选择题,共90分)
13.设函数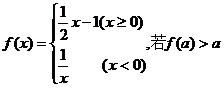 ,则实数
,则实数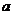 的取值范围是 .
的取值范围是 .
14.若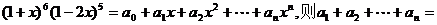 .
.
15.从0,1,2,3,4,5,6,7,8,9中取出3个数,使其和为不小于10的偶数,不同的取法共有 种(用数字作答).
16.已知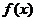 是定义在R上的奇函数,且是周期为2的周期函数,当
是定义在R上的奇函数,且是周期为2的周期函数,当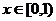 时,
时,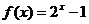 ,则
,则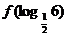 的值为 .
的值为 .
17.(本题12分)
已知点A(2,0)、B(0,2)、C(cosα,sinα),O为坐标原点,且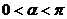 .
.
(1)若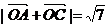 ,求
,求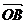 与
与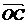 的夹角;
的夹角;
(2)若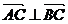 ,求tanα的值.
,求tanα的值.
|
18.(本小题12分)
已知 是等比数列,Sn是其前n项的和,a1,a7,a4成等差数列,求证:2S3,S6,S12-S6,成等比数列.
是等比数列,Sn是其前n项的和,a1,a7,a4成等差数列,求证:2S3,S6,S12-S6,成等比数列.
19.(本小题12分)
如图,正三棱柱ABC-A1B1C1中,D、E分别是BC、CC1的中点,AB=AA1.
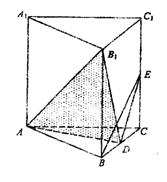 (1)求二面角B-AD-B1的正切值;
(1)求二面角B-AD-B1的正切值;
(2)证明:BE⊥平面AB1D;
(3)求异面直线DE与A1B1所成角的大小.
20.(本小题12分)
(理科答)A、B两队进行篮球决赛,共五局比赛,先胜三局者夺冠,且比赛结束。根据以往成绩,每场中A队胜的概率为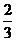 ,设各场比赛的胜负相互独立.
,设各场比赛的胜负相互独立.
(1)求A队夺冠的概率;
(2)设随机变量ξ表示比赛结束时的场数,求Eξ.
(文科答)甲、乙在罚球线投球命中的概率分别为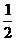 与
与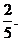
(1)甲、乙两人在罚球线各投球一次,求恰好命中一次的概率;
(2)甲、乙两人在罚球线各投球两次,求这四次投球中至少一次命中的概率.
21.(本题12分)
已知函数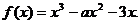
(1)若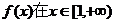 上是增函数,求实数a的取值范围;
上是增函数,求实数a的取值范围;
(2)若x=3是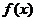 的极值点,求
的极值点,求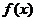 在
在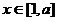 上的最小值和最大值.
上的最小值和最大值.
22.(本小题14分)
已知A、B、D三点不在一条直线上,且A(-2,0),B(2,0),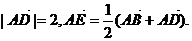
(1)求E点的轨迹方程;
(2)过A作直线交以A、B为焦点的随圆于M、N两点,线段MN的中点到y轴的距离为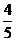 ,且直线MN与E点的轨迹相切,求椭圆的方程.
,且直线MN与E点的轨迹相切,求椭圆的方程.
高考数学复习双基统一测试 数 学 试 题 本试卷分第I卷(选择题)和II卷(非选择题)两部分,满分150分,考试时间120分钟。 参考公式:如果事件A、B互斥,那么P(A+B)=P(A)+P(B) 如果事件A、B相互独立,那么P(A.B)=P(A).P(B) 如果事件A在一次试验中发生的概率是P,那么n次独立重复试验中恰好发生k 次的概率Pn(k)= 球的体积公式:(其中R表示球的半径) 球的表面积公参考答案
参考答案
一、选择题
1.A 2.D 3.D 4.A 5.B 6.B 7.C 8.A 9.A 10.C 11.(理)B
(文)A 12.D
二、填空题
13.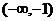 14.-65 15.51 16.
14.-65 15.51 16.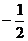
三、解答题
17.(本小题12分)
解:(1)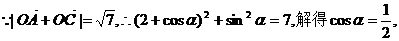 ……(2分)
……(2分)
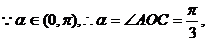
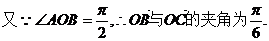 ……………………………………(4分)
……………………………………(4分)
(2)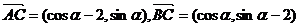
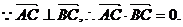
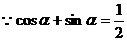 ①
①
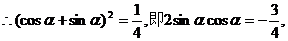 ………………………………(8分)
………………………………(8分)

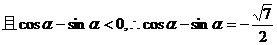 ②……………………(10分)
②……………………(10分)
由①②,得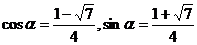
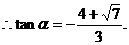 ………………………………………………………………(12分)
………………………………………………………………(12分)
18.(本小题12分)
[解法1]由已知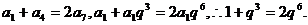 ………………(2分)
………………(2分)
当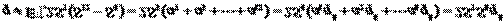
…………(4分)
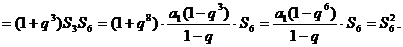 ………………(8分)
………………(8分)
当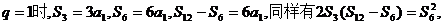 ……(10分)
……(10分)
所以,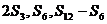 成等比数列.………………………………………………(12分)
成等比数列.………………………………………………(12分)
[解法2]由已知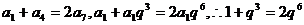 ,……………(2分)
,……………(2分)
当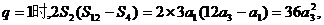
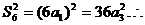
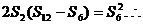
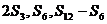 成等比数列.…(6分)
成等比数列.…(6分)
当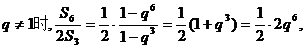 …………………………(8分)
…………………………(8分)
∴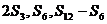 成等比数列.……………………………………………………(11分)
成等比数列.……………………………………………………(11分)
综上,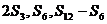 成等比数列.………………………………………………(12分)
成等比数列.………………………………………………(12分)
19.(本小题12分)
解:(1)在正三棱柱ABC-A1B1C1中,∵BD=DC,∴AD⊥BC,
又B1B⊥底面ABC,由三垂线定理,知AD⊥DB1
|
在Rt△B1BD中,tan∠B1DB=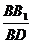 =2,
=2,
即二面角B-AD-B1的正切值为2.………………(4分)
(2)∵侧面BCC1B1为正方形,CE=EC1,BD=DE,
∴BE⊥DB1.………………………………(6分)
又AD⊥侧面BCC1B1,∴AD⊥BE,
∴BE⊥平面AB1D.…………………………(8分)
(3)取AC中点F,连FD,EF,∵A1B1∥AB∥DF,
∴∠EDF就是DE与A1B1所成的角.
设正三棱柱的各棱长均为2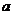 ,则DE=
,则DE=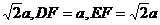 ,
,
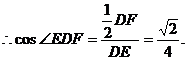
即DE与A1B1所成的角为 ……………………………………(12分)
……………………………………(12分)
20.(本小题12分)
(理科答)解:(1)A队连胜3场的概率为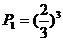 ,……………………(1分)
,……………………(1分)
打4场胜3场的概率为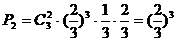 ,……………………(2分)
,……………………(2分)
打5场胜3场的概率为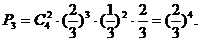 ……………………(4分)
……………………(4分)
又以上事件是互斥的,
∴A队获胜的概率为P=P1+P2+P3=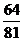 ……………………………………(6分)
……………………………………(6分)
(2)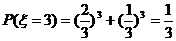 ,(A队连胜3场或B队连胜3场),……(7分)
,(A队连胜3场或B队连胜3场),……(7分)
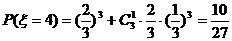 ;………………………………(8分)
;………………………………(8分)
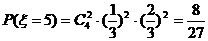 ;………………………………(10分)
;………………………………(10分)
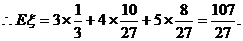 .………………………………(12分)
.………………………………(12分)
(文科答)解:(1)依题意,记“甲投一次命中”为事件A,“乙投一次命中”为事件B,
则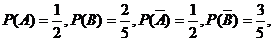 …………………………(2分)
…………………………(2分)
∵“甲、乙两人各投球一次,恰好命中一次”的事件为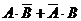 ,且为互斥事件,
,且为互斥事件,
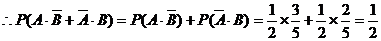 .………………(5分)
.………………(5分)
故甲、乙两人在罚球线各投球一次,恰好命中一次的概率为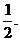 ………………(6分)
………………(6分)
(2)由于事件“甲、乙两人在罚球线各投球两次均不命中”的概率为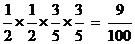 ,
,
…………………………(8分)
因此甲、乙两人在罚球线各投球两次至少有一个命的概率为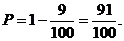 (12分)
(12分)
21.(本题12分)
解:(1)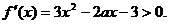
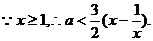 ……………………………………………………(2分)
……………………………………………………(2分)
设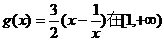 上是增函数,
上是增函数,
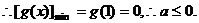 …………………………………………(6分)
…………………………………………(6分)
(2)由已知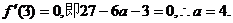 ……………………(8分)
……………………(8分)
易知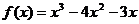 有极大值点
有极大值点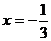 ,极小值点x=3,
,极小值点x=3,
此时,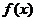 在[
在[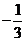 ,3]上是减函数,在[3,+∞
,3]上是减函数,在[3,+∞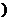 上是增函数.………………(10分)
上是增函数.………………(10分)
∴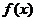 在[1,a]上的最小值是
在[1,a]上的最小值是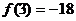 ,最大值是
,最大值是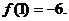 …………(12分)
…………(12分)
22.(本小题14分)
解:(1)设E点的坐标为( ),
),
 ,……………………(2分)
,……………………(2分)
∴E为BD的中点,OE为△ABD的中位线,
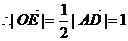 ,…………………………(4分)
,…………………………(4分)
即点E的轨迹方程是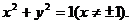 ………………………………(6分)
………………………………(6分)
|
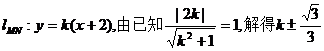 ,………………(6分)
,………………(6分)
即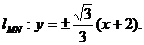
又椭圆方程为
由方程组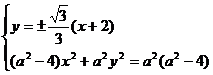
得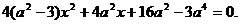 ………………(8分)
………………(8分)
设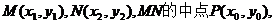
则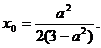
由已知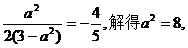
故所求的椭圆方程为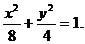 ………………………………(14分)
………………………………(14分)