(1)掌握椭圆的定义、标准方程和椭圆的简单几何性质，了解椭圆的参数方程.

(2)掌握双曲线的定义、标准方程和双曲线的简单几何性质.

(3)掌握抛物线的定义、标准方程和抛物线的简单几何性质.

(4)了解圆锥曲线的初步应用.

[注意]圆锥曲线是解析几何的重点，也是高中数学的重点内容，高考中主要出现三种类型的试题：①考查圆锥曲线的概念与性质；②求曲线方程和轨迹；③关于直线与圆锥曲线的位置关系的问题.

(一)椭圆及其标准方程

1.椭圆的定义：

椭圆的定义中，平面内动点与两定点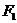、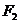的距离的和大于|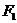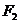|这个条件不可忽视.若这个距离之和小于|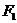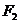|，则这样的点不存在；若距离之和等于|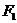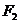|，则动点的轨迹是线段.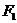

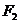2.椭圆的标准方程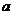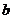：(＞＞0)

　

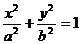
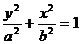
3.椭圆的标准方程判别方法：判别焦点在哪个轴只要看分母的大小：如果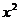项的分母大于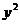项的分母，则椭圆的焦点在x轴上，反之，焦点在y轴上.

(二)椭圆的简单几何性质(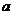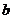＞＞0).

1．椭圆的几何性质：设椭圆方程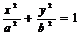

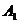
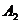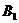
　线段、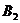分别叫做椭圆的长轴和短轴.它们的长分别等于2a和2b，

离心率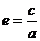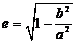： 　0＜e＜1.e越接近于1时，椭圆越扁；反之，e越接近于0时，椭圆就越接近于圆.

2.椭圆的第二定义

⑴ 定义：M与定点的距离和它到一条定直线的距离的比是常数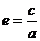，这个动点的轨迹是椭圆.

⑵准线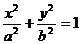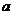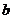： (＞＞0)的准线方程为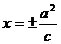. 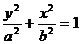准线方程.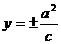

3.椭圆的焦半径：

　 ，.=+

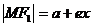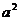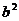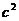
4.椭圆的参数方程

椭圆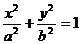(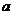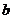＞＞0)

的参数方程为(θ为参数).

⑴ 这里参数θ叫做椭圆的离心角.椭圆上点P的离心角θ与直线OP的倾斜角α不同：；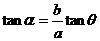

⑵ 椭圆的参数方程可以由方程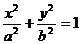与三角恒等式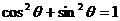相比较而得到，所以椭圆的参数方程的实质是三角代换.

5.椭圆的的内外部

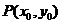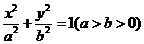点在椭圆的内部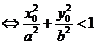

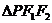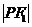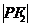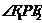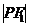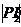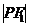
6.焦点三角形经常利用余弦定理、三角形面积公式将有关线段、、2c，有关角结合起来，建立+、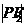等关系。面积公式：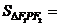　

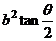
(三)双曲线及其标准方程

1双曲线的定义：

平面内与两个定点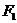、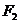的距离的差的绝对值等于常数2a(小于|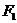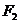|)的动点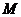的轨迹叫做双曲线.在这个定义中，要注意条件2a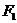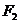＜||，这一条件可以用“三角形的两边之差小于第三边”加以理解.若2a=|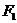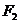|，则动点的轨迹是两条射线；若2a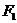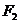＞||，则无轨迹.

　 若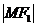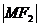＜时，动点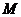的轨迹仅为双曲线的一个分支，又若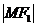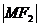＞时，轨迹为双曲线的另一支.而双曲线是由两个分支组成的，故在定义中应为“差的绝对值”.

2.双曲线的标准方程判别方法是：如果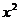项的系数是正数，则焦点在x轴上；如果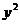项的系数是正数，则焦点在y轴上.对于双曲线，a不一定大于b，因此不能像椭圆那样，通过比较分母的大小来判断焦点在哪一条坐标轴上.

(四)双曲线的简单几何性质

1.双曲线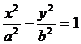实轴长为2a，虚轴长为2b，离心率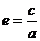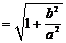离心率e越大，开口越大.

2.双曲线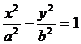的渐近线方程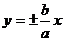为或表示为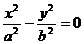.若已知双曲线的渐近线方程是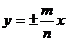，即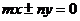，那么双曲线的方程具有以下形式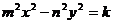：，其中k是

一个不为零的常数.

3.双曲线的第二定义：平面内到定点(焦点)与到定直线(准线)距离的比是一个大于1的常数(离心率)的点的轨迹叫做双曲线.

焦半径公式，.

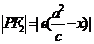4.双曲线的方程与渐近线方程的关系

(1)若双曲线方程为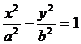

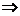
渐近线方程：.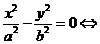

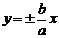(2)若渐近线方程为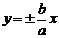

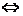
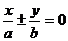
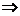
双曲线可设为.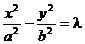

(3)若双曲线与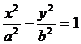有公共渐近线，可设为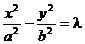(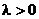，焦点在x轴上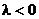，，焦点在y轴上).

(4)双曲线焦点三角形面积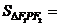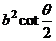：，高。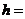

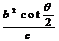(五)抛物线

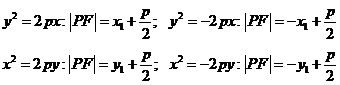抛物线的内外部

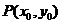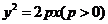点在抛物线的内部

.

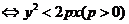(六)直线与圆锥曲线相交

1．弦长公式

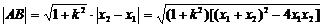
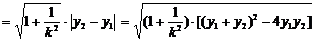抛物线y²=2px(p>0)的焦点弦

(1)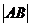＝x₁+x₂+p;(2)y₁y₂=－p²，x₁x₂=;

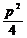过椭圆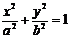(a>b>0)左焦点的焦点弦为AB，则，

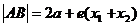2求轨迹的常用方法：

(1)直接法：直接通过建立x、y之间的关系，构成F(x,y)＝0；(2)待定系数法：(3)代入法(4)定义法：(5)参数法：

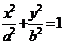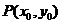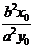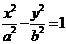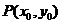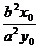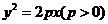3．圆锥曲线的中点弦问题：遇到中点弦问题常用“韦达定理”或“点差法”求解。在椭圆中，以为中点的弦所在直线的斜率k=－；在双曲线中，以为中点的弦所在直线的斜率k=；在抛物线中，以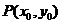为中点的弦所在直线的斜率k=。

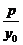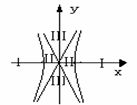
特别提醒：(1)务必别忘了检验！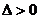

(2)简便的检验方法：如右图

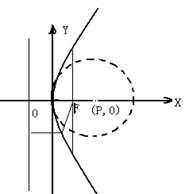
双曲线中点在渐近线和曲线上或它们之间的空隙区域，符合条件的方程都是增解；其它区域内的点为中点的弦的方程都符合题意

4．椭圆、双曲线的通径(过焦点且垂直于对称轴的弦)为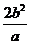，焦准距(焦点到相应准线的距离)为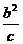，抛物线的通径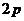为，焦准距为；