
1.设向量 ( )
( )
A.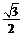 B.
B.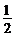 C.
C.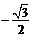 D.
D.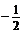
2.如果复数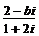 (其中
(其中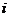 为虚数单位,
为虚数单位,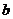 为实数)的实部和虚部是互为相反数,那么
为实数)的实部和虚部是互为相反数,那么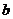 等于(
)
等于(
)
A.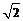 B.
B. C.2 D.
C.2 D.
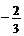
3.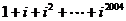 的值是 ( )
的值是 ( )
A.0 B.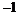 C.1 D.
C.1 D.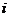
4.若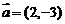 ,
, 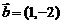 ,向量
,向量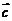 满足
满足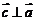 ,
,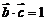 ,则
,则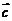 的坐标是 ( )
的坐标是 ( )
A.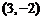 B.
B.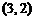 C.
C.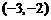 D.
D.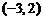
5.使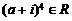 (
( 为虚数单位)的实数
为虚数单位)的实数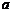 有 ( )
有 ( )
A.1个 B.2个 C.3个 D.4个
6.设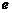 是单位向量,
是单位向量,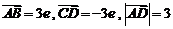 ,则四边形
,则四边形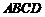 是
( )
是
( )
A.梯形 B.菱形 C.矩形 D.正方形
7.已知 、
、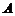 、
、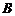 三点的坐标分别为
三点的坐标分别为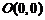 ,
,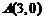 ,
,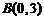 ,点
,点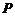 在线段
在线段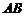 上,且
上,且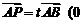 ≤
≤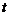 ≤
≤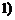 ,则
,则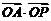 的最大值为 ( )
的最大值为 ( )
A.3 B.6 C.9 D.12
8.已知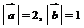 ,
,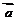 与
与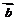 的夹角为
的夹角为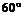 ,则使向量
,则使向量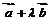 与
与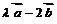 的夹角为钝角的实数
的夹角为钝角的实数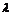 的取值范围是
( )
的取值范围是
( )
A. 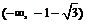 B.
B.
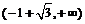
C. 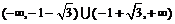 D.
D.
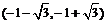
9.若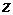 为复数,下列结论正确的是
( )
为复数,下列结论正确的是
( )
A.若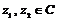 且
且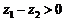 且
且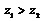 B.
B.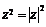
C.若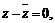 则
则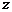 为纯虚数
D.若
为纯虚数
D.若 是正实数,那么
是正实数,那么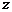 一定是非零实数
一定是非零实数
10.若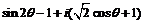 是纯虚数,则
是纯虚数,则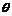 的值为 ( )
的值为 ( )
A.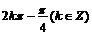 B.
B.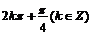 C.
C.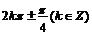 D.
D.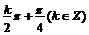
11.已知△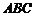 的三个顶点的
的三个顶点的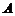 、
、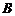 、
、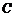 及平面内一点
及平面内一点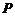 满足
满足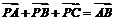 ,下列结论中正确的是 ( )
,下列结论中正确的是 ( )
A.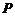 在△
在△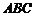 内部 B.
内部 B.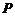 在△
在△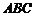 外部
外部
C.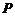 在
在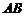 边所在直线上 D.
边所在直线上 D.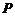 是
是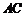 边的一个三等分点
边的一个三等分点
12.复数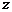 在复平面上对应的点在单位圆上,则复数
在复平面上对应的点在单位圆上,则复数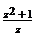 ( )
( )
A.是纯虚数 B.是虚数但不是纯虚数
C.是实数 D.只能是零
13.已知复数z满足等式: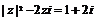 ,则z=
.
,则z=
.
14.把函数)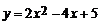 的图象按向量
的图象按向量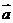 平移后,得到
平移后,得到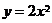 的图象,且
的图象,且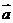 ⊥
⊥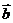 ,
,
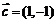 ,
,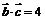 ,则
,则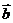 =_____________。
=_____________。
15.若复数z满足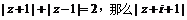 的最小值是___________.
的最小值是___________.
16.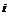 为虚数单位,复数
为虚数单位,复数 等于___________________.
等于___________________.
17.(本小题满分12分)已知向量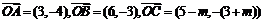 .
.
①若点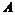 、
、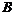 、
、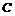 能构成三角形,求实数
能构成三角形,求实数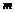 应满足的条件;
应满足的条件;
②若△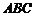 为直角三角形,且∠
为直角三角形,且∠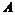 为直角,求实数
为直角,求实数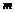 的值.
的值.
18.(本小题满分12分)已知向量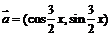 ,
,
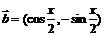 ,且
,且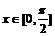 .
.
若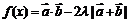 的最小值是
的最小值是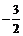 ,求
,求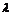 的值.
的值.
19.(本小题满分12分)已知向量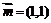 ,向量
,向量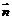 与向量
与向量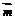 夹角为
夹角为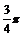 ,且
,且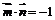 .
.
(1)求向量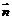 ;
;
(2)若向量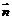 与向量
与向量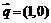 的夹角为
的夹角为 ,其中
,其中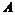 ,
,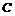 为
为
△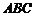 的内角,且
的内角,且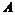 ,
,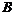 ,
,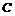 依次成等差数列,试求求|
依次成等差数列,试求求|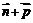 |的取值范围.
|的取值范围.
20.(本小题满分12分)已知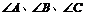 为
为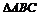 的三个内角,
的三个内角,
且 .
.
(1)当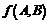 取得最小值时,求
取得最小值时,求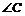 的度数;
的度数;
(2)当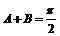 时,将函数
时,将函数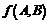 按向量
按向量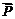 平移后得到函数
平移后得到函数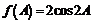 ,求向量
,求向量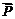 .
.
21.(本小题满分12分).已知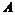 、
、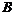 、
、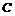 是△
是△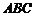 的三个内角,
的三个内角,
向量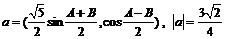 .
.
(1)求证: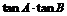 为定值;
为定值;
(2)求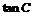 的最大值.
的最大值.
22.(本小题满分14分)已知向量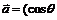 ,
,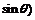 ,
,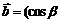 ,
,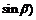 ,且
,且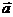 与
与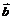 之
之
间有关系式: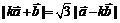 ,其中
,其中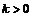 .
.
(1)试用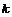 表示
表示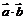 ;
;
(2)求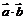 的最小值,并求此时
的最小值,并求此时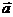 与
与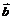 的夹角
的夹角 的值.
的值.
高考数学平面向量及复数专项训练(04)参考答案
参 考 答 案(四)
一、选择题:(1).A (2).D (3).C (4). C (5).C (6). B (7). C (8).D (9).D (10).B (11).D (12)C
二、填空题:(13). -1,-1-2i ; (14). (3,-1); (15). 1 ; (16). 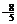
三、解答题:17.解 ①已知向量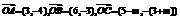 .若点A、B、C能构成三角形,则这三点不共线……2分
.若点A、B、C能构成三角形,则这三点不共线……2分
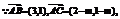 …5分 故知
…5分 故知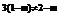 ∴实数
∴实数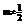 时,满足的条件…8分(若根据点A,B,C能构成三角形,必须|AB|+|BC|>|CA|…相应给分)②若△ABC为直角三角形,且∠A为直角,则
时,满足的条件…8分(若根据点A,B,C能构成三角形,必须|AB|+|BC|>|CA|…相应给分)②若△ABC为直角三角形,且∠A为直角,则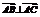 ,
,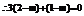 …………10分 解得
…………10分 解得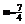 …………12分
…………12分
18.解: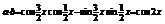 ……2分;
……2分; 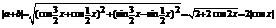 …4分
…4分
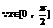 ∴
∴ ≥0,因此
≥0,因此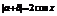 ∴
∴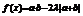 即
即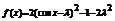 ……6分
……6分
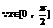 ∴0≤
∴0≤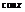 ≤1 ①若
≤1 ①若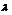 <0,则当且仅当
<0,则当且仅当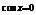 时,
时,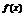 取得最小值-1,这与已知矛盾;…… 8分
②若0≤
取得最小值-1,这与已知矛盾;…… 8分
②若0≤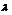 ≤1,则当且仅当
≤1,则当且仅当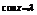 时,
时,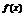 取得最小值
取得最小值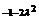 , 由已知得
, 由已知得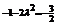 ,解得:
,解得: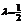 ……10分
③若
……10分
③若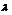 >1,则当且仅当
>1,则当且仅当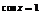 时,
时,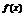 取得最小值
取得最小值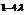 , 由已知得
, 由已知得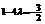 ,解得:
,解得: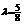 ,这与
,这与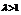 相矛盾.
综上所述,
相矛盾.
综上所述,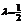 为所求.…… 12分
为所求.…… 12分
19. 解:(1)设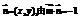 ,有
,有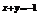 ① ………1分.因为
① ………1分.因为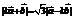 ,所以
,所以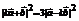 ,
,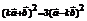 ,
,
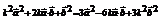 ,
,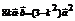
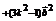 ,
, .……2分
.……2分
由(1)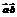
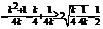 ,当且仅当
,当且仅当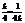 ,即
,即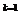 时取等号.此时
时取等号.此时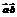
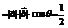 ∴
∴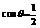 ∴
∴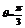 ,所以
,所以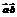 的最小值为
的最小值为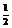 ,此时
,此时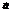 与
与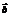 的夹角
的夹角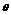 为
为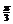 由
由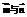 夹角为
夹角为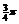 ,有
,有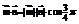 .∴
.∴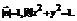 ②……3分
②……3分
由①②解得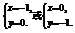 ∴即
∴即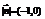 或
或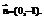 ……4分
……4分
(1)由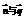 垂直知
垂直知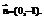 …5分.由2B=A+C知
…5分.由2B=A+C知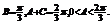 …6分若
…6分若 ,则
,则 …7分
…7分
∴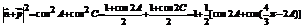

∵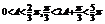 ,∴
,∴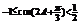 .
.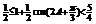 .即
.即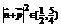 .∴
.∴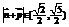 ……12分
……12分
20.解(1)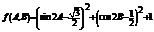 ,当
,当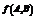 最小时,
最小时,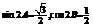
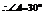 或60°,
或60°,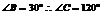 或90°
或90°
(2)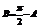 ,
,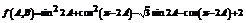
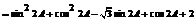
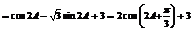 设
设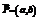 ,
,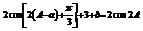 ,
, 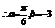
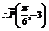
21.解:解:(理)(1)由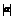 =
=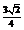 得:
得: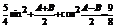 ,……2分 即:
,……2分 即: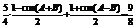 ,……2分
,……2分
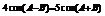 ……4分
……4分  ……6分
……6分
(2)由(1)得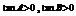 ,又
,又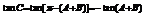 =
= ≤
≤ ……10分
……10分
当且仅当 .即A=B时,
.即A=B时,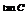 取得最大的值,此时
取得最大的值,此时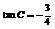 …12分
…12分
22. 解(1)因为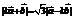 ,所以
,所以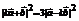 .
.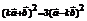 ,
,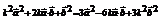 …3分
…3分
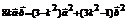 ,
,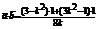
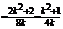 ……6分
……6分
(2)由(1)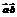
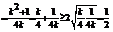 …9分当且仅当
…9分当且仅当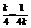 ,即
,即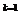 时取等号.…………10分
时取等号.…………10分
此时,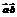
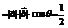 ,
,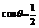 ,
,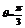 ,所以
,所以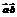 的最小值为
的最小值为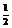 ,此时
,此时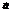 与
与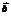 的夹角
的夹角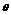 为
为 ……12分
……12分