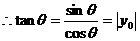1.(浙江卷)设向量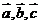 满足
满足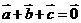 ,
,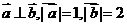 ,则
,则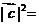
(A)1 (B)2 (C)4 (D)5
2. O是平面上一定点,A、B、C是平面上不共线的三个点,动点P满足
O是平面上一定点,A、B、C是平面上不共线的三个点,动点P满足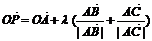 ,
,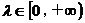 ,则P的轨迹一定通过△ABC的( )
,则P的轨迹一定通过△ABC的( )
(A)外心 (B)内心 (C)重心 (D)垂心
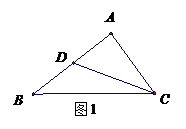
3.(广东卷)如图1所示,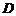 是
是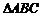 的边
的边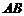 上的中点,则向量
上的中点,则向量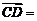
A.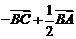 B.
B. 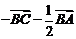 C.
C. 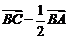 D.
D.
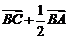
4.(湖南卷)已知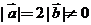 ,且关于
,且关于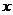 的方程
的方程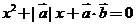 有实根,则
有实根,则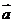 与
与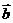 的夹角的取值范围是
( )A.[0,
的夹角的取值范围是
( )A.[0,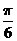 ]
B.
]
B.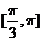 C.
C.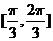 D.
D.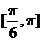
5.(全国卷I)已知向量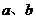 满足
满足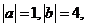 ,且
,且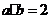 ,则
,则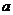 与
与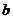 的夹角为
的夹角为
A.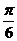 B.
B.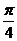 C.
C.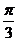 D.
D.
6.(山东卷)设向量a=(1, -2),b=(-2,4),c=(-1,-2),若表示向量4a,4b-2c,2(a-c),d的有向线段首尾相接能构成四边形,则向量d为
(A)(2,6) (B)(-2,6) (C)(2,-6) (D)(-2,-6)
7. (上海卷)如图,在平行四边形ABCD中,下列结论中错误的是 ( )
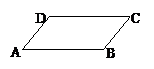 (A)
(A)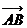 =
=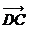 ;
(B)
;
(B)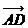 +
+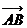 =
=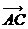 ;
;
(C)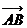 -
-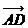 =
=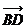 ; (D)
; (D)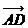 +
+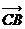 =
=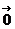 .
.
8.(北京卷)若三点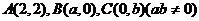 共线,则
共线,则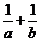 的值等于_________.
的值等于_________.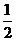
9.(2005年全国卷Ⅱ)点P在平面上作匀速直线运动,速度向量v=(4,-3)(即点P的运动方向与v相同,且每秒移动的距离为|v|个单位.设开始时点P的坐标为(-10,10),则5秒后点P的坐标为 (10,-5)
1.已知向量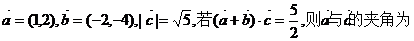 (
)
(
)
A 30° B 60° C 120° D 150°
2.已知点M1(6,2)和M2(1,7),直线y=mx-7与线段M1M2的交点分有向线段M1M2的比为3:2,则的值为 ( )
A 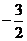 B
B 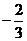 C
C 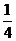 D 4
D 4
3.已知a,b是非零向量且满足(a-2b)⊥a,(b-2a)⊥b,则a与b的夹角是( )
A 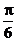 B
B 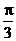 C
C 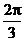 D
D 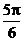
4.已知向量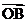 =(2,0),向量
=(2,0),向量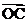 =(2,2),向量
=(2,2),向量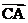 =(
=(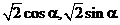 ),则向量
),则向量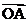 与向量
与向量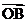 的夹角的范围为 ( )
的夹角的范围为 ( )
A [0,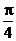 ] B [
] B [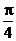 ,
,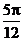 ] C [
] C [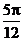 ,
,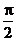 ] D [
] D [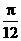 ,
,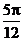 ]
]
5.设坐标原点为O,抛物线y2=2x与过焦点的直线交于A,B两点,则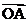 .
.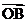 =( )
=( )
A 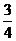 B
B 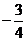 C 3 D -3
C 3 D -3
6.O是平面上一定点,A、B、C是平面上不共线的三个点,动点P满足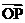 =
=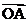 +λ(),
+λ(),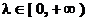 ,则点P的轨迹一定通过△ABC的(
)
,则点P的轨迹一定通过△ABC的(
)
A 外心 B 内心 C 重心 D 垂心
7.点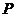 在平面上作匀速直线运动,速度向量
在平面上作匀速直线运动,速度向量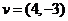 (即点
(即点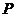 的运动方向与
的运动方向与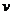 相同,且每秒移动的距离为
相同,且每秒移动的距离为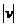 个单位).设开始时点
个单位).设开始时点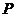 的坐标为(-10,10),则5秒后点
的坐标为(-10,10),则5秒后点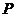 的坐标为( )
的坐标为( )
A (-2,4) B (-30,25) C (10,-5) D (5,-10)
8.已知向量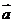 ≠
≠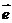 ,|
,|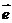 |=1,对任意t∈R,恒有|
|=1,对任意t∈R,恒有|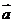 -t
-t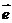 |≥|
|≥|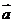 -
-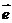 |,则( )
|,则( )
A 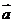 ⊥
⊥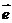 B
B 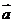 ⊥(
⊥(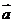 -
-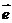 ) C
) C 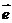 ⊥(
⊥(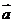 -
-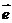 ) D (
) D (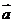 +
+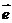 )⊥(
)⊥(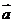 -
-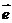 )
)
9.P是△ABC所在平面上一点,若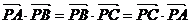 ,则P是△ABC的(D )
,则P是△ABC的(D )
A 外心 B 内心 C 重心 D 垂心
10.△ABC中,若a4+b4+c4=2c2(a2+b2),则∠C度数是:
A 600 B 450或1350 C 1200 D 300
11.已知向量a=(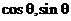 ),向量b=(
),向量b=(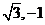 ),则|2a-b|的最大值是
),则|2a-b|的最大值是
12.把函数y=2x2-4x+5的图像按向量a平移,得到y=2x2的图像,且a⊥b,c=(1,-1),b.c=4,则b=
13.已知平面上三点A、B、C满足|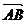 |=3,|
|=3,|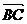 |=4,|
|=4,|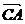 |=5,则
|=5,则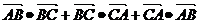 的值等于 .
的值等于 .
14.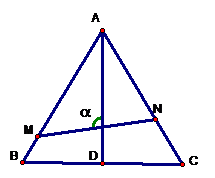 在
在 中,O为中线AM上一个动点,若AM=2,则
中,O为中线AM上一个动点,若AM=2,则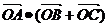 的最小值是_____.
的最小值是_____.
15.已知向量a=(sinθ,1),b=(1,cosθ),-<θ<.
(Ⅰ)若a⊥b,求θ;(Ⅱ)求|a+b|的最大值.
16.06年江西卷)如图,已知△ABC是边长为1的正三角形,M、N分别是
边AB、AC上的点,线段MN经过△ABC的中心G,
设ÐMGA=a( )
)
(1) 试将△AGM、△AGN的面积(分别记为S1与S2)
表示为a的函数
(2) 求y=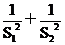 的最大值与最小值
的最大值与最小值
17.已知定点F(1,0),动点P在y轴上运动,过点P作PM交x轴于点M,并延长MP至点N,且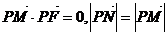 .(1)求动点N的轨迹方程;
.(1)求动点N的轨迹方程;
(2)直线l与动点N的轨迹交于A、B两点,若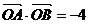 且4
且4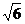 ≤
≤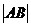 ≤
≤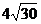 ,求直线l的斜率的取值范围.
,求直线l的斜率的取值范围.
18.已知两点M(-1,0), N(1 , 0),且点P使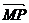 .
.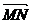 ,
,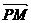 .
.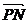 ,
,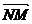 .
.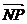 成公差小于零的等差数列.(Ⅰ)点P 的轨迹是什么曲线?
成公差小于零的等差数列.(Ⅰ)点P 的轨迹是什么曲线?
(Ⅱ)若点P坐标为(x0、y0),记θ为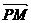 与
与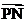 的夹角,求tanθ.
的夹角,求tanθ.
答案与提示:
1.C 提示:设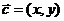 ,则
,则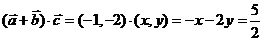 ,又
,又
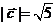 ,所以
,所以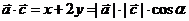 ,得
,得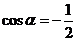 ,
,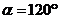 ,
,
2. D 提示:设交点M(x,y),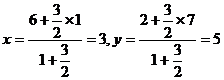 ,代入直线方程可得.
,代入直线方程可得.
3. B 提示:a2-2b•a=0且b2-2a•b=0,相减得|a|=|b|,代入其中一式即可.
4. D 提示:点C的轨迹是以(2,2)为圆心,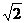 为半径的圆.
为半径的圆.
5. B 提示:设A(x1,y1),B(x2,y2),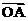 .
.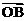 =x1x2+y1y2=
=x1x2+y1y2=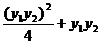 ,将直线方程y=k(x-0.5)代入抛物线方程消去x可得y1y2.
,将直线方程y=k(x-0.5)代入抛物线方程消去x可得y1y2.
6. B 提示: 表示
表示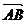 方向上的单位向量,
方向上的单位向量,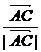 表示
表示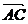 方向上的单位向量,
方向上的单位向量,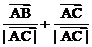 在∠BAC的平分线上,故P点的轨迹过三角形的内心.
在∠BAC的平分线上,故P点的轨迹过三角形的内心.
7.C 提示:设5秒后点P运动到点A,则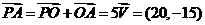 ,
,
∴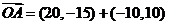 =(10,-5).
=(10,-5).
8.C 提示:由|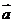 -t
-t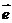 |≥|
|≥|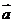 -
-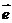 |得|
|得|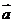 -t
-t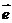 |2≥|
|2≥|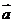 -
-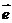 |2,展开并整理得
|2,展开并整理得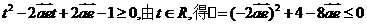 ,得
,得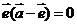 ,即
,即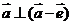 .
.
9.D 提示:由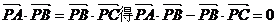 .
.
即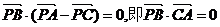 , 则
, 则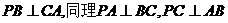
所以P为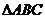 的垂心.
的垂心.
10.B 提示:由a4+b4+c4=2c2(a2+b2)得:a4+b4+c4-2a2c2-2b2c2+2a2b2=2a2b2,即(a2+b2-c2)2=2a2b2
a2+b2-c2=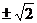 ab,
ab,
11. 4
12. (3, -1)
13.-25 提示:因AB⊥BC,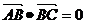 ,
,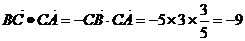 ,
,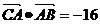 ,所以原式=0-9-16=-25
,所以原式=0-9-16=-25
14.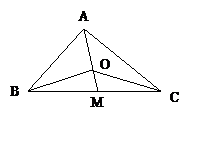 -2 提示:如图,
-2 提示:如图,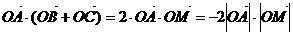
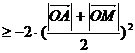 ,当
,当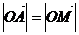 取等号.
取等号.
即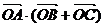 的最小值为:-2.
的最小值为:-2.
15. 解:(Ⅰ)若a⊥b,则sinθ+cosθ=0,由此得 tanθ=-1(-<θ<),所以 θ=-;
(Ⅱ)由a=(sinθ,1),b=(1,cosθ)得|a+b|=
==,
当sin(θ+)=1时,|a+b|取得最大值,即当θ=时,|a+b|最大值为+1.
16. 解:因为G是边长为1的正三角形ABC的中心,
解:因为G是边长为1的正三角形ABC的中心,
所以
AG=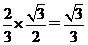 ,ÐMAG=
,ÐMAG=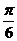 ,
,
由正弦定理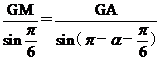 ,得
,得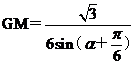
则S1=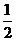 GM.GA.sina=
GM.GA.sina=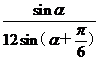 同理可求得S2=
同理可求得S2=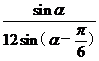
(1) y=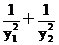 =
=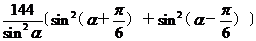
=72(3+cot2a)因为 ,所以当a=
,所以当a=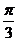 或a=
或a=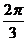 时,y取得最大值ymax=240
时,y取得最大值ymax=240
当a= 时,y取得最小值ymin=216
时,y取得最小值ymin=216
17. 略解 (1)y2=4x (x>0) (2)先证明l与x轴不垂直,再设l的方程为
y=kx+b(k≠0),A(x1,y1),B(x2,y2).联立直线与抛物线方程,得
ky2- 4y+4b=0,由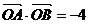 ,得
,得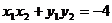 .
.
又 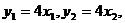 故
故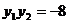 而
而
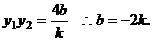
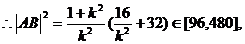
解得直线l的斜率的取值范围是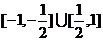
18.略解(Ⅰ)设点P(x , y),分别计算出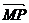 .
.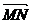 ,
,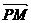 .
.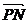 ,
,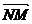 .
.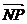 ,
,
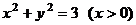 由题意,可得点P的轨迹方程是
由题意,可得点P的轨迹方程是
故点P 的轨迹是以原点为圆心、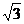 为半径的右半圆.
为半径的右半圆.
(Ⅱ) 由(Ⅰ)知,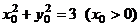 ,可得cosθ=
,可得cosθ=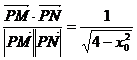 ,
,
又x0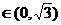 ,∴
,∴ 即
即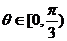 ,
,
于是sinθ=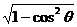 =
=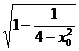 =
=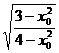 =
=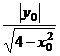 ,
,