
1. 在
在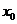 处的导数(或变化率或微商)
处的导数(或变化率或微商)
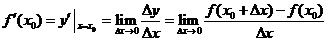 .
.
2.瞬时速度
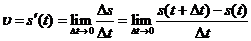 .
.
3.瞬时加速度
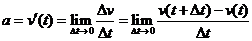 .
.
4. 在
在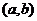 的导数
的导数
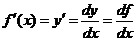
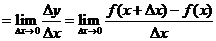 .
.
5. 函数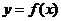 在点
在点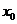 处的导数的几何意义
处的导数的几何意义
函数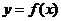 在点
在点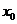 处的导数是曲线
处的导数是曲线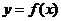 在
在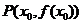 处的切线的斜率
处的切线的斜率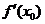 ,相应的切线方程是
,相应的切线方程是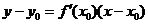 .
.
6.几种常见函数的导数
(1) 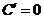 (C为常数).
(C为常数).
(2) 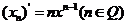 .
.
7.判别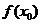 是极大(小)值的方法当函数
是极大(小)值的方法当函数 在点
在点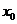 处连续时,
处连续时,
(1)如果在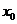 附近的左侧
附近的左侧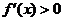 ,右侧
,右侧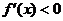 ,则
,则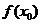 是极大值;
是极大值;
(2)如果在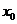 附近的左侧
附近的左侧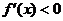 ,右侧
,右侧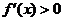 ,则
,则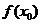 是极小值.
是极小值.
1.导数的定义:f(x)在点x0处的导数记作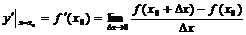 ;
;
2.根据导数的定义,求函数的导数步骤为:(1)求函数的增量
(2)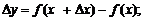 (2)求平均变化率
(2)求平均变化率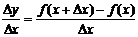 ;
;
(3)取极限,得导数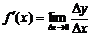 ;
;
3..导数的几何意义:曲线y=f(x)在点P(x0,f(x0))处的切线的斜率是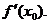 相应地,
相应地,
切线方程是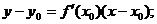
4.导数的应用:
(1)利用导数判断函数的单调性:设函数y=f(x)在某个区间内可导,
如果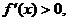 那么f(x)为增函数;
那么f(x)为增函数;
如果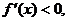 那么f(x)为减函数;
那么f(x)为减函数;
如果在某个区间内恒有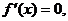 f(x)为常数;
f(x)为常数;
(2)求可导函数极值的步骤:
①求导数 ;
;
②求方程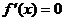 的根;
的根;
③检验 在方程
在方程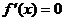 根的左右的符号,如果左正右负,那么函数y=f(x)在这个根处取得最大值;如果左负右正,那么函数y=f(x)在这个根处取得最小值;
根的左右的符号,如果左正右负,那么函数y=f(x)在这个根处取得最大值;如果左负右正,那么函数y=f(x)在这个根处取得最小值;
5导数与函数的单调性的关系
㈠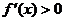 与
与 为增函数的关系。
为增函数的关系。
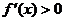 能推出
能推出 为增函数,但反之不一定。㈡
为增函数,但反之不一定。㈡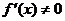
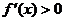 与
与 为增函数的关系。
为增函数的关系。
若将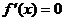 的根作为分界点,因为规定
的根作为分界点,因为规定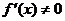 ,即抠去了分界点,此时
,即抠去了分界点,此时 为增函数,就一定有
为增函数,就一定有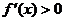 。∴当
。∴当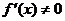 时,
时,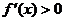 是
是 为增函数的充分必要条件。
为增函数的充分必要条件。
㈢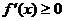 与
与 为增函数的关系。
为增函数的关系。
 为增函数,一定可以推出
为增函数,一定可以推出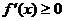 ,但反之不一定,因为
,但反之不一定,因为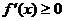 ,即为
,即为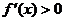 或
或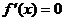 。当函数在某个区间内恒有
。当函数在某个区间内恒有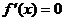 ,则
,则 为常数,函数不具有单调性。∴
为常数,函数不具有单调性。∴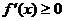 是
是 为增函数的必要不充分条件。
为增函数的必要不充分条件。
7.函数的单调性:如果函数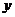 =
= 在某个区间内可导,那么若
在某个区间内可导,那么若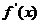 >0,则
>0,则 为增函数;
为增函数;
若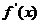 <0则
<0则 为减函数;若
为减函数;若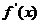 =0则
=0则 为常数;
为常数;
说明:利用导数可以证明或判断函数的单调性,注意当f ’(x)≥0或f ’(x)≤0,带上等号。
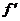 (x0)=0是函数f(x)在x0处取得极值的非充分非必要条件。
(x0)=0是函数f(x)在x0处取得极值的非充分非必要条件。
8.函数的极值
①极值定义:如果函数 在点
在点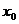 附近有定义,那么对
附近有定义,那么对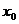 附近的点,都有
附近的点,都有 <
<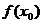 我们就说
我们就说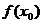 函数的一个极大值,记作
函数的一个极大值,记作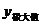 =
=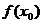 ;
;
 在点
在点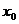 附近的点,都有
附近的点,都有 >
>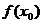 我们就说
我们就说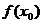 函数的一个极小值,记作
函数的一个极小值,记作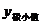 =
=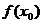 ;极大值与极小值统称为极值。
;极大值与极小值统称为极值。
②极值判别法:当函数 在点
在点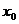 处连续时,极值判断法是:
处连续时,极值判断法是:
如果在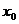 附近的左侧
附近的左侧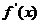 >0,右侧
>0,右侧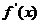 <0,那么
<0,那么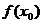 是极大值;
是极大值;
如果在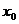 附近的左侧
附近的左侧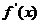 <0,右侧
<0,右侧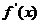 >0,那么
>0,那么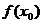 是极小值。
是极小值。
③求可导函数极值的步骤:
首先:求导数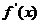 ;再求导数
;再求导数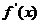 =0的根;最后:检查
=0的根;最后:检查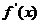 在方程根左右的值的符号,如果左正右负,那么
在方程根左右的值的符号,如果左正右负,那么 在这个根处取极大值;如果左负右正,那么
在这个根处取极大值;如果左负右正,那么 在这个根处取极小值。
在这个根处取极小值。
说明:曲线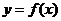 在
在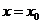 处有极值
处有极值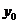 ,可以说明以下四个内容:
,可以说明以下四个内容:
①点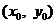 在曲线上,满足
在曲线上,满足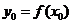 ;②该处导数
;②该处导数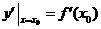 =0;
=0;
③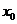 是方程
是方程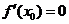 的根;
的根;
④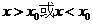 ,
, 符号各异。
符号各异。
9函数的最大值与最小值
在闭区间[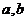 ]上连续,在(
]上连续,在(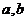 )内可导,
)内可导, 在[
在[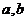 ]上求最大值与最小值的步骤:
]上求最大值与最小值的步骤:
先求 在(
在(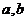 )内的极值;再将
)内的极值;再将 的各极值与
的各极值与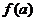 、
、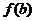 比较,其中最大的一个是最大值,最小的一个是最小值。
比较,其中最大的一个是最大值,最小的一个是最小值。
说明:利用导数求最值的步骤:
(1)求导数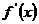 ;
;
(2)求方程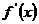 =0的根
=0的根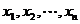
(3)计算极值及端点函数值的大小;(4)根据上述值的大小,确定最大值与最小值.