
1、已知集合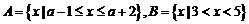 ,则能使
,则能使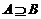 成立的实数
成立的实数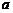 的取值范围是(
)
的取值范围是(
)
A.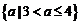 B.
B.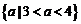 C.
C.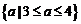 D.
D.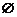
2、等比数列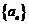 中,
中,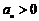 且
且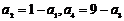 ,则
,则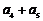 等于( )
等于( )
A.16
B.27
C.36
D.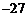
3、不等式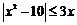 的解集为( )
的解集为( )
A.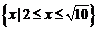 B.
B. C.
C.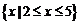 D.
D.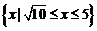
4、曲线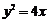 关于直线
关于直线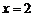 对称的曲线方程是(
)
对称的曲线方程是(
)
A.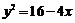 B.
B.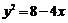 C.
C.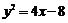 D.
D.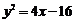
5、已知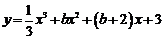 是
是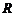 上的单调增函数,则
上的单调增函数,则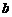 的范围(
)
的范围(
)
A.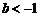 或
或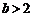 B.
B.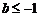 或
或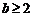 C.
C.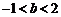 D.
D.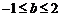
6、直线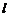 是双曲线
是双曲线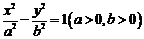 的右准线,以原点为圆心且过双曲线的焦点的圆被直线
的右准线,以原点为圆心且过双曲线的焦点的圆被直线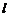 分成弧长为
分成弧长为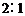 的两段圆弧,则该双曲线的离心率是( )
的两段圆弧,则该双曲线的离心率是( )
A.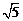 B.
B.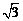 C.
C.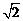 D.
D.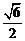
7、空间四点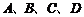 ,若直线
,若直线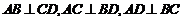 同时成立,则
同时成立,则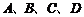 四点的位置关系是( )
四点的位置关系是( )
A.一定共面 B.一定不共面 C.不一定共面 D.这样的四点不存在
8、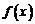 是定义在
是定义在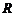 上的奇函数,它的最小正周期为
上的奇函数,它的最小正周期为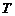 ,则
,则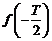 的值为( )
的值为( )
A.0
B.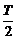 C.
C.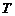 D.
D.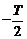
9、已知实数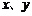 满足
满足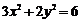 ,则
,则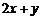 的最大值为( )
的最大值为( )
A.4 B.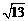 C.
C. D.
D.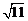
10、 函数
函数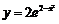 的图象大致是(
)
的图象大致是(
)
选择题答案栏
11、直线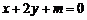 按向量
按向量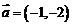 平移后与圆
平移后与圆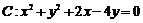 相切,则实数
相切,则实数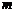 的值为____________.
的值为____________.
12、在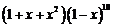 的展开式中,
的展开式中,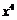 项的系数是_______________.
项的系数是_______________.
13、12名同学分别到三个不同的路口进行车流量的调查,若每个路口4人,则不同的分配方案共有____________
14、函数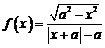 是奇函数的充要条件是____________
是奇函数的充要条件是____________
15、 ,
,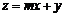 取得最大值的最优解有无数个,则
取得最大值的最优解有无数个,则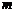 等于
等于
16、在下列四个命题中,①函数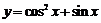 的最小值是
的最小值是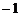 。②函数
。②函数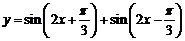 的最小正周期是
的最小正周期是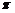 。③已知
。③已知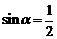 ,且
,且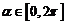 ,则
,则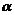 的取值集合为
的取值集合为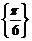 。④函数
。④函数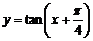 的定义域是
的定义域是 。把你认为正确命题的序号填在指定的位置上。_______________.
。把你认为正确命题的序号填在指定的位置上。_______________.
高考数学客观题限时训练二
班级 姓名 学号 记分
1.若集合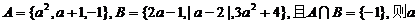 =
=
A.-1 B.0或1 C.2 D.0
2.若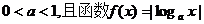 ,则下列各式中成立的是
,则下列各式中成立的是
A.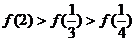 B.
B.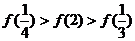
C.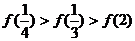 D.
D.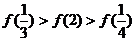
3.在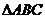 中,如果
中,如果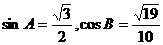 ,则角A等于
,则角A等于
A.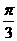 B.
B.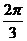 C.
C.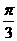 或
或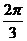 D.
D.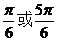
4.在等差数列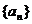 中,若
中,若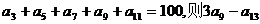 的值为
的值为
A.20 B.30 C.40 D.50
5.直线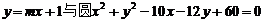 有交点,直线不过圆心,则
有交点,直线不过圆心,则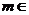
A.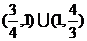 B.
B.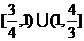 C.
C.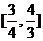 D.
D.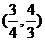
6.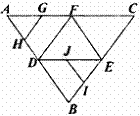 如图,在正三角形
如图,在正三角形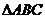 中,D、E、F分别为各边的中点,G、
中,D、E、F分别为各边的中点,G、
H、I、J分别为AF,AD,BE,DE的中点,将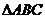 沿DE,
沿DE,
EF,DF折成三棱锥以后,GH与IJ所成角的度数为 ( )
A.90° B.60°
C.45° D.0°
7.不等式组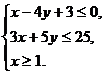 所表示的平面区域图形是 ( )
所表示的平面区域图形是 ( )
A.第一象限内的三角形 B.四边形
C.第三象限内的三角形 D.以上都不对
8. 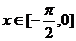 ,则函数
,则函数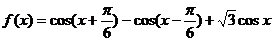 的最小值是
的最小值是
A.1 B.-1 C.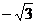 D.-2
D.-2
9.一个正四面体外切于球O1,同时又内接于球O2,则球O1与球O2的体积之比为
A.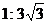 B.
B.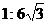 C.
C.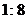 D.
D.
10.若把英语单词“hello”的字母顺序写错了,则可能出现的错误的种数是 ( )
A.119 B.59 C.120 D.60
11.E,F是随圆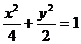 的左、右焦点,l是椭圆的一条准线,点P在l上,则∠EPF的最大值是 ( )
的左、右焦点,l是椭圆的一条准线,点P在l上,则∠EPF的最大值是 ( )
A.15° B.30° C.60° D.45°
12.关于甲、乙、丙三人参加高考的结果有下列三个正确的判断:①若甲未被录取,则乙、丙都被录取;②乙与丙中必有一个未被录取;③或者甲未被录取,或者乙被录取,则三人中被录取的是 ( )
A.甲 B.丙 C.甲与丙 D.甲与乙
选择题答案栏
13.把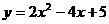 的图象按向量a平移后,得
的图象按向量a平移后,得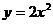 的图象,则a=
的图象,则a=
14.已知关于x的不等式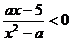 的解集为M,若
的解集为M,若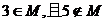 ,则实数a的取值范围是
.
,则实数a的取值范围是
.
15.设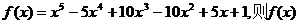 的反函数的解析式是
的反函数的解析式是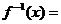
16.若E,F分别是四棱柱ABCD-A1B1C1D1的棱AB,AD
的中点,则加上条件 ,
就可得结论:EF⊥平面DA1C1. (写出你认为正确的一个
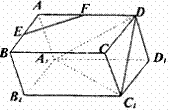 条件即可)
条件即可)
高考数学客观题限时训练三
班级 姓名 学号 记分
1.设全集U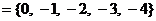 , 集合M
, 集合M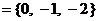 , N
, N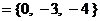 , 那么(CUM)
, 那么(CUM)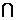 N为
N为
A.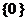 B.
B.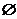 C.
C.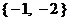 D.
D.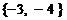
2.等差数列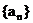 前四项和为40, 末四项和为72, 所有项和为140, 则该数列共有
前四项和为40, 末四项和为72, 所有项和为140, 则该数列共有
A.9项 B.12项 C.10项 D.13项
3.已知平面向量与向量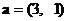 ,
,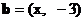 , 且
, 且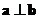 , 则
, 则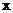 =
=
A.3 B.1 C.-1 D.-3
D.-3
4.一平面截一球得到直径是6cm的圆面, 球心到这个平面的距离是4cm , 则该球的体积是
A.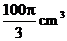 B.
B.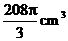
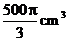 D.
D.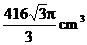
5.函数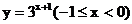 的反函数是
的反函数是
A.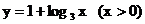 B.
B.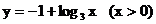
C.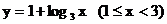 D.
D.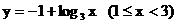
6. 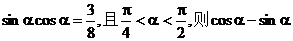 的值是
的值是
A.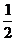 B.-
B.-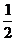 C.
C.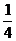 D.-
D.-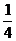
7.已知抛物线的顶点为原点, 焦点在y轴上, 抛物线上点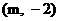 到焦点的距离为4, 则m的值为
到焦点的距离为4, 则m的值为
A.4 B.-2 C.4或-4 D.2或-2
8.函数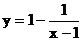
A.在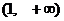 内单调递增 B.在
内单调递增 B.在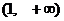 内单调递减
内单调递减
C.在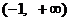 内单调递增 D.在
内单调递增 D.在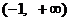 内单调递减
内单调递减
9.若P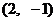 为圆
为圆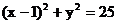 的弦AB的中点, 则直线AB的方程是
的弦AB的中点, 则直线AB的方程是
A.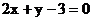 B.
B.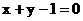
C.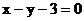 D.
D.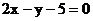
10.拟定从甲地到乙地通话m分钟的电话费由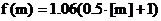 (元)决定, 其中
(元)决定, 其中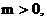
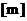 是大于或等于m的最小整数, (如
是大于或等于m的最小整数, (如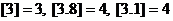 ), 则从甲地到乙地通话时间为5.5分钟的电话费为
), 则从甲地到乙地通话时间为5.5分钟的电话费为
A.3.71元 B.3.97元 C.4.24元 D.4.77元
11.已知2a+1<0,关于x的不等式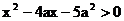 的解集是
的解集是
A.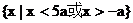 B.
B.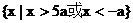
C.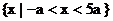 D.
D.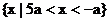
12.设函数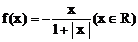 ,区间M=[a,b]
,区间M=[a,b]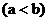 , 集合N={
, 集合N={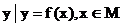 },则使M=N成立的实数对 (a, b)有
A.0个 B.1个 C.2个 D.无数多个
},则使M=N成立的实数对 (a, b)有
A.0个 B.1个 C.2个 D.无数多个
选择题答案栏
13.设a、b、c分别是△ABC的∠A、∠B、∠C的对边边长, 则直线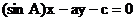 与直线
与直线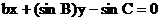 的夹角大小是
.
的夹角大小是
.
14.已知椭圆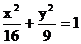 的左、右焦点分别为
的左、右焦点分别为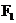 、
、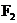 , 点P在椭圆上. 若
, 点P在椭圆上. 若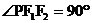 是一个直角三角形的三个顶点, 则点P到x轴的距离为
.
是一个直角三角形的三个顶点, 则点P到x轴的距离为
.
15.已知a、b为不垂直的异面直线, 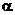 是一个平面, 则a、b在
是一个平面, 则a、b在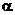 上的射影有可能是①两条平行直线 ②两条互相垂直的直线 ③同一条直线
④一条直线及其外一点称在上面结论中, 正确结论的编号是 .(写出所有正确结论)
上的射影有可能是①两条平行直线 ②两条互相垂直的直线 ③同一条直线
④一条直线及其外一点称在上面结论中, 正确结论的编号是 .(写出所有正确结论)
16.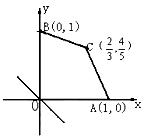 给出平面区域如图所示,
目标函数为:
给出平面区域如图所示,
目标函数为: 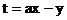
若当且仅当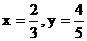 时, 目标函数t取最小值,
时, 目标函数t取最小值,
则实数a的取值范围是 .
高考数学客观题限时训练四
班级 姓名 学号 记分
1. 设实数集R为全集,集合P={x|f (x)=0},Q={x|g (x)=0},H={x|h(x) =0},则方程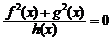 的解集是
A.
的解集是
A.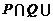 ∁RH B.
∁RH B.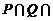 ∁RH C.
∁RH C.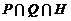 D.
D.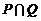
2. 在等差数列{an}中,若a4+a6+a8+a10+a12=120,则2 a10-a12的值为 A.20 B.22 C.24 D.28
3. 函数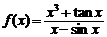 的奇偶性是
A.是奇函数不是偶函数 B.是偶函数不是奇函数
C.既是奇函数又是偶函数 D.既不是奇函数也不是偶函数
的奇偶性是
A.是奇函数不是偶函数 B.是偶函数不是奇函数
C.既是奇函数又是偶函数 D.既不是奇函数也不是偶函数
4. 设O是平面上任意一点,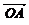 =a,
=a,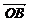 =b,
=b,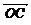 =ma+nb (m、n∈R),若A、B、C三点共线,则m、n满足
A.m+n=-1 B.m+n=1 C.m+n=0 D.m-n=1
=ma+nb (m、n∈R),若A、B、C三点共线,则m、n满足
A.m+n=-1 B.m+n=1 C.m+n=0 D.m-n=1
5.
要使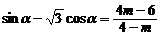 有意义,则m范围是
A.m≤
有意义,则m范围是
A.m≤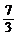 B.m≥-1
C.m≤-1或m≥
B.m≥-1
C.m≤-1或m≥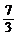 D.-1≤m≤
D.-1≤m≤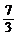
6. 设P=1+5(x+1)+10 (x+1)2+10(x+1) 3+5(x+1) 4+(x+1) 5,则P等于 A.x5 B.(x+2)5 C.(x-1) 5 D.(x+1) 5
7. 若a、b∈R,则下列不等式:①a2+3>2a;②a2+b2≥2(a-b-1);③a5+b5>a3b2+a2b3;④a+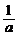 ≥2.其中一定成立是
A.①②③ B.①②④ C.①② D.②④
≥2.其中一定成立是
A.①②③ B.①②④ C.①② D.②④
8. 若函数f (x)的定义域为(0,+∞),且f (x)>0,f / (x)>0,那么函数y=xf (x) A.存在极大值 B.存在极小值 C.是增函数 D.是减函数
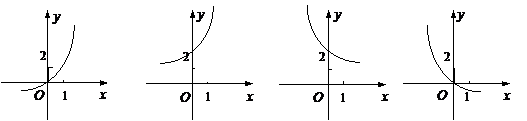
9. 已知函数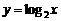 的反函数是
的反函数是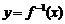 ,则函数
,则函数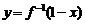 的图象是
A B C D
的图象是
A B C D
10. 在6个电子产品中,有两个次品,4个合格品,每次任取一个测试,测试完后不放回,直到两个次品都找到为止,那么经过四次测试恰好将两个次品全部找出来的概率是
A.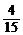 B.
B.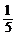 C.
C.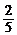 D.
D.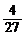
11. 直线y=m(m为常数)与正切曲线y= (
(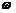 >0)相交,则相邻两个交点的距离是
A.
>0)相交,则相邻两个交点的距离是
A.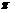 B.
B.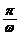 C.
C.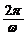 D.
D.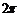
12. 若函数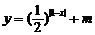 的图象与x轴有公共点,则m的取值范围是
A.m≤-1 B.-1≤m<0 C.m≥1 D.0<m≤ 13若sin2α<0,sin α-cos α>0,则cos α
的图象与x轴有公共点,则m的取值范围是
A.m≤-1 B.-1≤m<0 C.m≥1 D.0<m≤ 13若sin2α<0,sin α-cos α>0,则cos α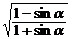 +sin α
+sin α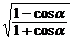 = .
= .
14不等式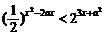 对一切实数x都成立,则a的取值范围是 .
对一切实数x都成立,则a的取值范围是 .
15采用简单随机抽样从个体数为6的总体中抽取一个容量为3的样本,则每个个体被抽到的概率为 .
16设 是函数
是函数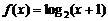 的反函数,若
的反函数,若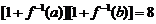 ,则f (a+b)的值为 .
,则f (a+b)的值为 .
选择题答案栏
高考数学客观题限时训练五
班级 姓名 学号 记分
1.给出下列函数:①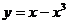 ,②
,②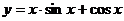 ,③
,③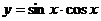 ,
,
④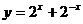 ,其中是偶函数的有 ( )
,其中是偶函数的有 ( )
A.1个 B.2个 C.3个 D.4个
2.若α、β终边关于y轴对称,则下列等式成立的是 ( )
A.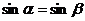 B.
B.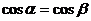
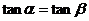 D.
D.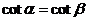
 3.设全集U=R,
3.设全集U=R,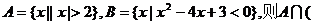 B)是 ( )
B)是 ( )
A.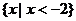 B.
B.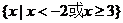 C.
C.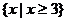 D.
D.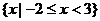
4.函数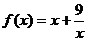 的单调递增区间是 ( )
的单调递增区间是 ( )
A.(-3,3)B.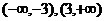 C.(-3,+∞)D.(-3,0),(0,3)
C.(-3,+∞)D.(-3,0),(0,3)
5.设等比数列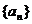 的前n项和为Sn,若
的前n项和为Sn,若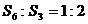 ,则
,则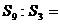 ( )
( )
A.1:2 B.2:3 C.3:4 D.1:3
6.若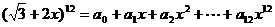 ,则
,则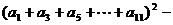
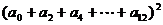 的值是 ( )
的值是 ( )
A.1 B.-1 C.2 D.-2
7.在平面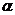 内的两条直线
内的两条直线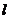 、
、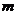 都平行于平面
都平行于平面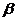 是平面
是平面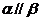 的 ( )
的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.不充分也不必要条件
8.把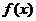 =3x的反函数
=3x的反函数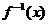 图象向右平移2个单位就得到曲线C,函数
图象向右平移2个单位就得到曲线C,函数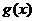 的图象与曲线C关于
的图象与曲线C关于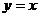 成轴对称,那么
成轴对称,那么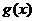 等于 ( )
等于 ( )
A.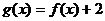 B.
B.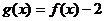
C.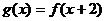 D.
D.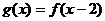
9.已知点A为双曲线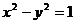 的顶点,点B和点C在双曲线的同一分支上,且A与B在y轴的异侧,则正△ABC的面积是 ( )
的顶点,点B和点C在双曲线的同一分支上,且A与B在y轴的异侧,则正△ABC的面积是 ( )
A.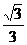 B.
B.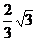 C.
C.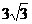 D.
D.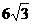
10.设坐标原点为O,抛物线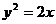 与过其焦点的直线交于两点A、B,则
与过其焦点的直线交于两点A、B,则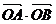 等于A.
等于A.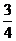 B.
B.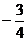 C.-3 D.3
C.-3 D.3
11.记函数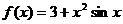 在区间[-2,2]上的最大值为M,最小值为m,那么M+m的值为 A.0 B.3 C.6 D.8
在区间[-2,2]上的最大值为M,最小值为m,那么M+m的值为 A.0 B.3 C.6 D.8
12.13年前有一笔扶贫助学资金,每年的存款利息(年利率11.34%,不扣税)可以资助100人上学,平均每人每月94.50元。现在(存款年利率1.98%,并且扣20%税)用同样一笔资金每年的存款利息最多可以资助( )人上学(平均每人每月100元).A.10 B.13 C.15 D.20
13.若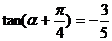 则
则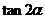 的值是
.
的值是
.
14.一个单位有职工360人,其中业务人员276人,管理人员36人,后勤人员48人.为了了解职工的住房情况,要从中抽取一个容量为30的样本,则应该采用 的抽样方法,且应从后勤人员中抽取 人.
15.某学校要从高三的6个班中派9名同学参加市中学生外语口语演讲,每班至少派1人,则这9个名额的分配方案共有 种.(用数字作答)
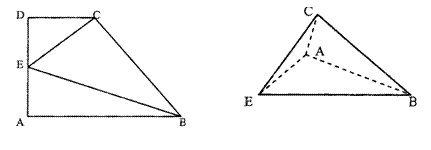
16.一直角梯形ABCD,AB⊥AD,AD⊥DC,AB=2,BC=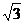 ,CD=1,E为AD中点,沿CE、BE把梯形折成四个面都是直角三角形的三棱锥,使点A、D重合,则这三棱锥的
,CD=1,E为AD中点,沿CE、BE把梯形折成四个面都是直角三角形的三棱锥,使点A、D重合,则这三棱锥的
体积等于 .
选择题答案栏
高考数学客观题限时训练六
班级 姓名 学号 记分
1.已知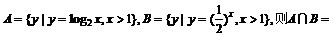 ( )
( )
A.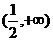 B.(
B.(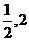 ) C.
) C.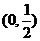 D.(0,2)
D.(0,2)
2.下列函数中,最小正周期为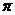 ,且图象关于直线
,且图象关于直线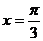 对称的是 ( )
对称的是 ( )
A.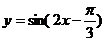 B.
B.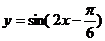 C.
C.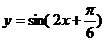 D.
D.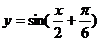
3.若不等式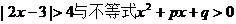 的解集相同,则
的解集相同,则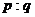 等于 ( )
等于 ( )
A.12 : 7 B.7 : 12 C.(-12 : 7) D.(-3): 4
4.已知函数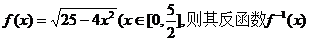 为 ( )
为 ( )
A.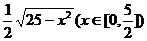 B.
B.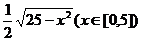
C.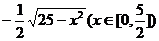 D.
D.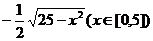
5.等差数列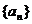 的前n项和为
的前n项和为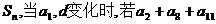 是一个定值,那么下列各数中也为定值的是A.S13;B.S15 C.S7 D.S8
是一个定值,那么下列各数中也为定值的是A.S13;B.S15 C.S7 D.S8
6.要得到函数 的图象,只要将函数
的图象,只要将函数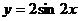 的图象 ( )
的图象 ( )
A.向左平移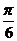 B.向右平移
B.向右平移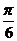 C.向左平移
C.向左平移 D.向右平移
D.向右平移
7.若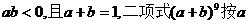 降幂展开后,其第二项不大于第三项则实数a的取值范围为 ( )
降幂展开后,其第二项不大于第三项则实数a的取值范围为 ( )
A.(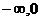 ) B.
) B.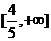 C.
C.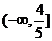 D.(1,+
D.(1,+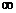 )
)
8.已知向量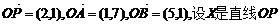 上的一点(O为坐标原点),那么
上的一点(O为坐标原点),那么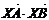 的最小值是A.-16 B.-8 C.0 D.4 ( )
的最小值是A.-16 B.-8 C.0 D.4 ( )
9.2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较小的锐角为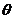 ,
,
大正方形的面积是1,小正方形的面积是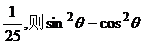 的值等于
的值等于
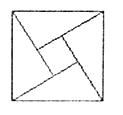 A.1 B.
A.1 B.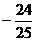 C.
C.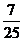 D.-
D.-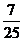
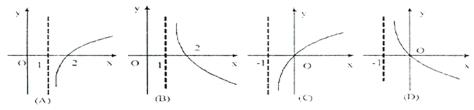
10.若奇函数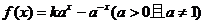 在R上是增函数,那么
在R上是增函数,那么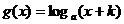 的大致图像是
的大致图像是
11.一文艺演出中,需给舞台上方安装一排彩灯共15只,以不同的点亮方式增加舞台效果,要求设计者按照每次点亮时,必须有6只是关的,且相邻的灯不能同时被关掉,两端的灯必须点亮的要求进行设计,那么不同点亮方式的种数是A.28 B.84 C.180 D.360
12.由方程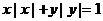 确定的函数
确定的函数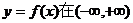 上是 (
)
上是 (
)
A.奇函数 B.偶函数 C.增函数 D.减函数
13.已知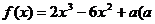 为常数)在[-2,2]上有最小值3,那么
为常数)在[-2,2]上有最小值3,那么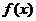 在[-2,2]上的最大值是
.
在[-2,2]上的最大值是
.
14.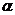 为锐角,
为锐角,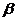 为钝角,
为钝角,
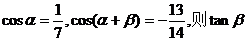 =( )
=( )
15.已知数列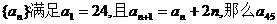 =
.
=
.
16.如图是某企业几年来关于生产销售的一张统计图表,关于该企业近几年的销售情况,有以下几种说法:
①这几年该企业的利润逐年提高;(注:利润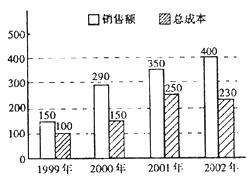 =销售额-总成本);
=销售额-总成本);
②1999年至2000年是该企业销售额增长最快的一年;③2000年至2001年是该企业销售额增长最慢的一年;④2001年至2002年该企业销售额增长最慢,但由于总成本有所下降,因而2002年该企业的利润比上一年仍有所增长.
其中说法正确的是 (注:把你认为是正确的说法的序号都填上).
高考数学客观题限时训练七
班级 姓名 学号 记分
1.已知集合M={a,0},N={x|2x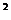 -5x<0,x∈z},若M∩N≠
-5x<0,x∈z},若M∩N≠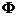 ,则a等于 ( )
,则a等于 ( )
A.1
B.2 C.1或2 D.1或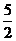
2.一枚硬币连掷三次至少出现一次正面的概率为 ( )
A. B.
B.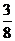 C.
C.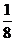 D.
D.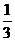
3.已知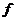 (x)=ax
(x)=ax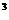 +3x
+3x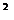 +2,若
+2,若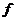 ′(-1)=4,则a的值等于 (
)
′(-1)=4,则a的值等于 (
)
A. 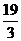 B.
B.
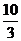 C.
C.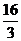 D.
D.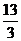
4.已知а、b是直线,а、β、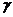 是平面,给出下列命题:①а∥а,а∥β,а∩β=b,则а∥b;②а⊥
是平面,给出下列命题:①а∥а,а∥β,а∩β=b,则а∥b;②а⊥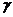 ,β⊥
,β⊥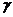 ,则а∥β;③а⊥а,b⊥β,а⊥b,则а⊥β;④а∥β,β∥
,则а∥β;③а⊥а,b⊥β,а⊥b,则а⊥β;④а∥β,β∥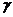 ,а⊥а,则а⊥
,а⊥а,则а⊥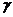 ,其中错误的命题的序号是
,其中错误的命题的序号是
A.① B.② C.③ D.④
5.已知双曲线等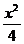 +
+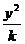 =1的离心率e<2,则k的取值范围是
( )
=1的离心率e<2,则k的取值范围是
( )
A.k<0或k>3 B.-3<k<0 C.-12<k<0 D.-8<k<3
6.若向量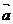 =(COSа,sinа),
=(COSа,sinа),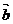 = (COSβ,sinβ),则
= (COSβ,sinβ),则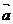 与
与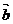 一定满足
( )
一定满足
( )
A.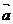 与
与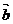 的夹角等于а-β B.(
的夹角等于а-β B.(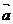 +
+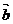 )⊥(
)⊥(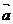 -
-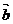 )
)
C. ∥
∥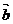 D.
D.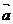 ⊥
⊥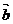
7.下列命题中,使命题M是命题N成立的充要条件的一组命题是 ( )
A.M:a>b; N:ac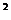 >bc
>bc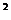 B.M:a>b,c>d,N:a-d>b-c
B.M:a>b,c>d,N:a-d>b-c
C.M:a>b>0,c>d>0,N:ac>bd D.M:|a-b|=|a|+|b|,N:ab≤O
8.某商场对顾客实行购物优惠活动,规定一次购物:(1)如不超过200元,则不予优惠;(2)如超过200元但不超过500元的按9折优惠;(3)如超过500元,其中500元按9折给予优惠,超过500元的部份给予8折优惠。某人两次去购物,分别付款168元和423元,若他只去一次购买同样价值的商品,则应付款
A. 472.8元 B. 510.4元 C. 522.8元 D. 560.4元
9.圆x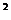 +y
+y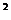 -4x-2y+c=0与y轴交于A、B两点,圆心为P,若
-4x-2y+c=0与y轴交于A、B两点,圆心为P,若 APB=90°,则c的值为( )A.8 B.3 C.-
APB=90°,则c的值为( )A.8 B.3 C.-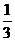 D.-3
D.-3
10.数列2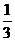 ,4
,4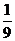 ,6
,6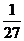 ,…,2n
,…,2n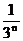 ,…的前n项和为S
,…的前n项和为S ,则
,则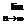
 的值等于 ( ) A.1
B.0 C.2 D.
的值等于 ( ) A.1
B.0 C.2 D.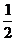
11.满足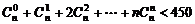 的最大自然数
的最大自然数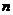 等于
等于
A. 4 B. 5 C. 6 D. 7
12.一盛满水的三棱锥容器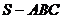 ,不久后发现三条侧棱上各有一个小洞
,不久后发现三条侧棱上各有一个小洞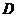 、
、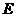 、
、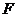 ,且已知
,且已知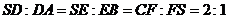 若仍用这个容器盛水,则最多可盛原来水的
若仍用这个容器盛水,则最多可盛原来水的
A. 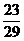 B.
B. 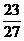 C.
C. 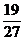 D.
D. 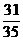
选择题答案栏
13.某高校的某一专业从8名优秀毕业生中选派5名支援中国西部开发建设,某人必须被选派的种数是________________。
14.设抛物线y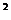 =4x的一条弦AB以P(
=4x的一条弦AB以P(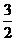 ,1)为中点,则该弦所在直线的斜率为_______。
,1)为中点,则该弦所在直线的斜率为_______。
15.已知两异面直线a、b所成的角为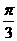 ,直线
,直线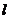 分别与a、b所成的角都是
分别与a、b所成的角都是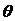 ,则
,则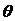 的取值范围是_____________________。
的取值范围是_____________________。
16.某地区重视环境保护,绿色植被面积呈上升趋势,经调查,从1989年到1998年这10年间每两年上升2%,1997年和1998年这两年种植植被815×10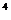 m
m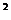 ,当地政府决定今后四年内仍按这一比例发展下去,那么从1999年到2002年种植植被面积为_______(保留整数)。
,当地政府决定今后四年内仍按这一比例发展下去,那么从1999年到2002年种植植被面积为_______(保留整数)。
高考数学客观题限时训练八
班级 姓名 学号 记分
1.
已知函数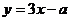 ,它的反函数是
,它的反函数是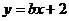 ,则
,则
A.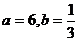 B.
B.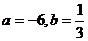 C.
C. 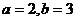 D.
D.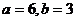
2. 函数 周期是 奇偶性情况是
周期是 奇偶性情况是
A.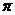 、奇函数; B.
、奇函数; B. 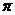 、偶函数;C. 2
、偶函数;C. 2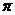 、奇函数;D. 2
、奇函数;D. 2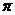 、偶函数
、偶函数
3.命题甲: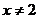 或
或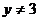 ;命题乙:
;命题乙: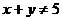 ,则甲是乙的
,则甲是乙的
A.充分非必要条件; B.必要非充分条件;
C.充要条件; D.既不是充分条件,也不是必要条件.
4.不等式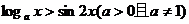 对任意
对任意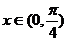 都成立,则
都成立,则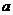 的取值范围为A.
的取值范围为A.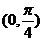 B.
B.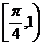 C.
C.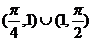 D.
D.
5.双曲线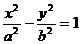 的一条准线被它的两条渐近线所截得线段长度恰好等于它的一个焦点到一条渐近线的距离,则双曲线的离心率为
的一条准线被它的两条渐近线所截得线段长度恰好等于它的一个焦点到一条渐近线的距离,则双曲线的离心率为
A.3 B.2 C.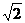 D.
D.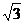
6.已知函数f (x)的导数为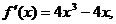 且图象过点(0,-5),当函数f (x)取得极大值-5时,x的值应为
且图象过点(0,-5),当函数f (x)取得极大值-5时,x的值应为
A.-1 B.0 C.1 D.±1
7.若四面体的六条棱中,有五条棱长为a,则该四面体的体积的最大值为 A.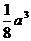 B.
B.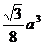 C.
C.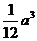 D.
D.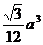
8.不等式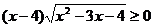 的解集是
的解集是
A.  B.
B. 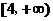 C.
C.
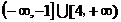 D.
D. 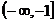
9.数列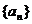 满足
满足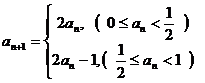 ,若
,若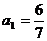 ,则
,则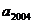 =
=
A.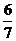 B.
B. 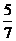 C.
C.
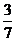 D.
D.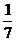
10.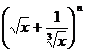 的各项系数之和大于8,小于32,则展开式中系数最大的项是
的各项系数之和大于8,小于32,则展开式中系数最大的项是 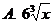
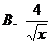
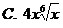
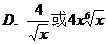
11.定义集合 的新运算:
的新运算: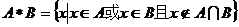 ,则
,则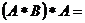
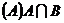
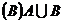
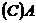
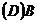
12.已知向量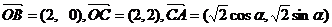 ,则
,则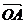 与
与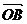 夹角的范围是A.
夹角的范围是A.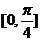 B.
B.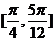 C.
C.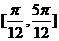 D.
D.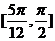
选择题答案栏
13.已知直线 平行,则直线
平行,则直线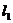 的倾斜角的大小是 (用反三角符号表示).
的倾斜角的大小是 (用反三角符号表示).
14.已知函数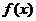 满足:
满足: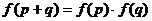 ,
,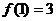 ,则
,则
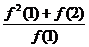 +
+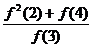 =
=
15.一个田径队,有男运动员56人,女运动员42人,比赛后,立即用分层抽样的方法,从全体队员中抽出一个容量为28的样本进行尿样兴奋剂检查,其中男运动员应抽___________人.
16. 已知正方体ABCD-A1B1C1D1的棱长为单位1,黑白两个蚂蚁从点A出发沿棱向前爬行,每走完一条棱称为“走完一段”。白蚂蚁爬地的路线是AA1→A1D1→……,黑蚂蚁爬行的路线是AB→BB1→……,它们都遵循如下规则:所爬行的第i+2与第i段所在直线必须是异面直线(其中i是正整数).设白,黑蚂蚁都走完2005段后各停止在正方体的某个顶点处,这时黑,白两蚂蚁的距离是
高考数学客观题限时训练九
班级 姓名 学号 记分
1、已知f(x)=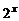 ,则f -1(
,则f -1(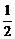 )=( )
)=( )
(A)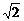 (B)-1 (C)
(B)-1 (C)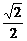 (D)
(D)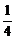
2、一个单位职工150人,其中有业务人员110人,管理人员15人,后勤服务人员25人。为了了解职工的某种情况,要从中抽取一个容量为30的样本,则应抽取管理人员 ( )A、15人 B、5人 C、3人 D、2人
3、已知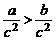 ,则下列不等式一定成立的是( )
,则下列不等式一定成立的是( )
(A)a2>b2 (B)ln a>ln b (C)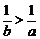 (D)
(D)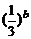 >
>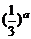
4、如果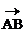 =a,
=a,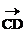 =b,,则a=b是四点A、B、D、C构成平行四边形的 条件.
=b,,则a=b是四点A、B、D、C构成平行四边形的 条件.
(A)充分非必要;(B)必要不充分 (C)充要 (D)既不充分也不必要
5、已知{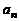 }的前n项和Sn=n2-4n+1,则|a1|+|a2|+…+|a10|=( )
}的前n项和Sn=n2-4n+1,则|a1|+|a2|+…+|a10|=( )
(A)67 (B)65 (C)61 (D)56
6.下列函数中,最小正周期为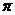 ,且图象关于直线
,且图象关于直线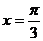 对称的是 ( )
对称的是 ( )
A.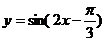 B.
B.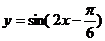
C.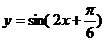 D.
D.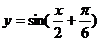
7、方程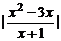 =
=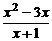 的解集是
(
)
的解集是
(
)
(A)(-1,0)∪(3,+∞) (B)(-∞,-1)∪(0,3)
(C)(-1,0]∪[3,+∞) (D)(-∞,-1)∪[0,3]
8、曲线y=2x-x3在横坐标为-1的点处的切线为l,则点(3,2)到l的距离等于
A、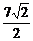 B、
B、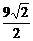 C、
C、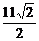 D、
D、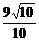 (
)
(
)
9、已知cos(α-β)=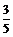 ,sinβ=-
,sinβ=-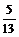 ,且α∈(0,
,且α∈(0,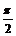 ),β∈(-
),β∈(-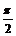 ,0)则
,0)则
sinα=( )(A)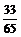 (B)
(B) (C)-
(C)-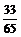 (D)-
(D)-
10、已知x、y满足 ,则z=x+y的最大值为
(
)
,则z=x+y的最大值为
(
)
(A)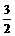 (B)4 (C)1 (D)2
(B)4 (C)1 (D)2
11、等差数列{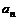 }与{
}与{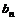 }的前n项和分别为
}的前n项和分别为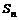 与
与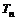 ,且
,且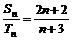 ,则
,则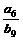 =
=
(A)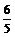 (B)
(B) (C)1 (D)
(C)1 (D)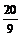 (
)
(
)
12、由等式x 4+a1x3+a2x2+a3x+a4=(x+1)4+b1(x+1)3+b2(x+1)2+b3(x+1)+b4。定义映射f:(a1,a2,a3,a4)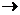 (b1,b2,b3,b4),则f(4,3,2,1)等于(
)
(b1,b2,b3,b4),则f(4,3,2,1)等于(
)
A、(1,2,3,4) B、(0,3,4,0)
C、(-1,0,2,-2) D、(0,-3,4,-1)
选择题答案栏
13、若球的体积是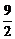 π,则其表面积为
π,则其表面积为
14、等比数列{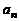 }中,a4+a6=3,则a5(a3+2a5+a7)=
}中,a4+a6=3,则a5(a3+2a5+a7)=
15、某物体一天中的温度T是时间t的函数,T(t)=t3-3t+60,时间单位是小时,温度单位是℃。t=0时表示12时,其后t取正值。则上午9时该物体的温度为 ℃
16、关于函数f(x)=2sin(3x-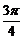 ),有下列命题:
),有下列命题:
①其最小正周期是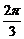 ;②其图象可由y=2sin3x向左平移
;②其图象可由y=2sin3x向左平移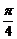 个单位得到;
个单位得到;
③其表达式可改写为y=2cos(3x-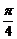 );④在x∈[
);④在x∈[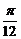 ,
,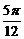 ]上为增函数。
]上为增函数。
其中正确的命题的序号是
高考数学客观题限时训练十
班级 姓名 学号 记分
1.已知a为不等于零的实数,那么集合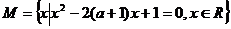 的子集的个数为
的子集的个数为
A.1个 B.2个 C.4个 D.1个或2个或4个
2.函数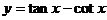 的最小正周期是
的最小正周期是
A.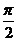 B.π
C.2π
D.3π
B.π
C.2π
D.3π
3.已知关于x的不等式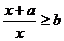 的解集是[-1,0)则a+b=
的解集是[-1,0)则a+b=
A.-2 B.-1 C.1 D.3
4.过双曲线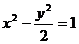 的右焦点作直线l交双曲线于A、B两点,若
的右焦点作直线l交双曲线于A、B两点,若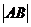 =4,则满足条件的直线l有
=4,则满足条件的直线l有
A.2条 B.3条 C.4条 D.无数条
5.若向量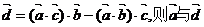 的夹角是
的夹角是
A.30° B.60° C.90° D.120°
6.设a、b是两条异面直线,P是a、b外的一点,则下列结论正确的是
A.过P有一条直线和a、b都平行;B.过P有一条直线和a、b都相交;
C.过P有一条直线和a、b都垂直;D.过P有一个平面和a、b都垂直。
7.互不相等的三个正数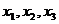 成等比数列,且点
成等比数列,且点
P1(
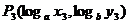 共线
共线
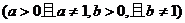 则
则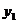 ,
,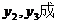
A.等差数列,但不等比数列; B.等比数列而非等差数列
C.等比数列,也可能成等差数列 D.既不是等比数列,又不是等差数列
8.若从集合P到集合Q=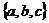 所有的不同映射共有81个,则从集合Q到集合P可作的不同映射共有
所有的不同映射共有81个,则从集合Q到集合P可作的不同映射共有
A.32个 B.27个 C.81个 D.64个
9.对于函数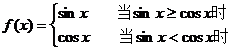 给出下列四个命题:
给出下列四个命题:
①该函数的值域为[-1,1]
②当且仅当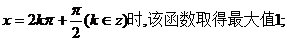
③该函数是以π为最小正周期的周期函数;
④当且仅当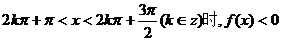 上述命题中错误命题的个数为A.1
B.2
C.3
D.4
上述命题中错误命题的个数为A.1
B.2
C.3
D.4
10.已知球的表面积为20π,球面上有A、B、C三点,如果AB=AC=2,BC=2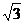 ,则球心到平面ABC的距离为
,则球心到平面ABC的距离为
A.1 B.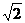 C.
C.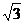 D.2
D.2
11.设x、y满足约束条件: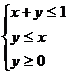 则
则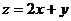 的最大值为
的最大值为
A.1 B.2 C.3 D.4
12.已知等差数列 ,那么,A.
,那么,A.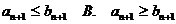 C、
C、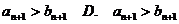
选择题答案栏
13.椭圆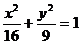 中,以点M(一1,2)为中点的弦所在直线方程是___________。
中,以点M(一1,2)为中点的弦所在直线方程是___________。
14.在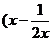 )
)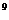 的展开式中,x3的系数是_________。
的展开式中,x3的系数是_________。
15.在△ABC中,边AB为最长边,且sinA.sinB=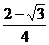 ,则cosA.cosB的最大值是
。
,则cosA.cosB的最大值是
。
16.一项“过关游戏”规则规定:在第n关要抛掷一颗骰子n次,如果这n次抛掷所出现的点数之和大于n2,则算过关,那么,连过前二关的概率是。_______。
高考数学客观题限时训练十一
班级 姓名 学号 记分
1.已知f(x)=sinx+cosx,则f( )的值为
)的值为
A.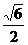 B.
B.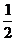 C.
C.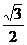 D.
D.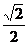
2.若 <
< <0,则下列结论不正确的是
<0,则下列结论不正确的是
A.a2<b2 B.ab<b2
C.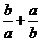 >2 D.|a|+|b|>|a+b|
>2 D.|a|+|b|>|a+b|
3.已知a,b,c为任意非零向量,下列命题中可作为a=b的必要不充分的条件是
①|a|=|b|;②(a)2=(b)2;③c.(a-b)=0.
A.①② B.②③
C.①②③ D.①
4.从6人中任选4人排成一排,其中甲、乙必入选,且甲必须排在乙的左边(可以不相邻),则所有不同排法种数是
A.36 B.72
C.144 D.288
5.正项等比数列{an}满足:a2.a4=1,S3=13,bn=log3an,则数列{bn}的前10项的和是 A.65 B.-65 C.25 D.-25
6.椭圆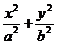 =1(a>b>0)的长轴被圆x2+y2=b2与x轴的两个交点三等分,则椭圆的离心率是 A.
=1(a>b>0)的长轴被圆x2+y2=b2与x轴的两个交点三等分,则椭圆的离心率是 A.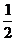 B.
B.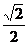 C.
C.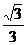 D.
D.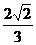
7.甲、乙、丙投篮一次命中的概率分别为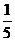 、
、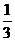 、
、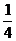 ,现三人各投篮一次至少有1人命中的概率为
,现三人各投篮一次至少有1人命中的概率为
A.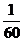 B.
B.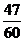 C.
C.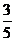 D.
D.
8.正四面体棱长为1,其外接球的表面积为
A.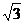 π B.
π B.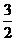 π
C.
π
C.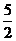 π D.3π
π D.3π
9.如图,正四棱柱ABCD-A1B1C1D1,底面边长为1,侧棱长为2,E为BB1中点,则异面直线AD1与A1E所成的角为
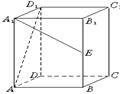 A.arccos
A.arccos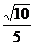 B.arcsin
B.arcsin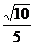
C.90° D.arccos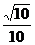
10.已知,命题p:x+ 的最小值是2,q:(1-x)5的展开式中第4项的系数最小,下列说法正确的是
的最小值是2,q:(1-x)5的展开式中第4项的系数最小,下列说法正确的是
A.命题“p或q”为假 B.命题“p且q”为真
C.命题“非p”为真 D.命题q为假
11.已知f(x)为奇函数,周期T=5,f(-3)=1,且tanα=2,则f(20sinαcosα)的值为
A.1 B.-1 C.2 D.-2
12.已知f(x)=3x-b(2≤x≤4,b为常数)的图象经过点(2,1),则
F(x)=[f-1(x)]2-f-1(x2)的值域为
A.[2,5] B.[1,+∞) C.[2,10] D.[2,13]
选择题答案栏
13.若双曲线离心率为2,则它的两条渐近线的夹角等于_________.
14.已知函数y=f(x)的反函数f-1(x)=log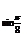 (x-cos2
(x-cos2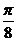 ),则方程f(x)=1的解是_________.
),则方程f(x)=1的解是_________.
15.对于实数x、y,定义新运算x*y=ax+by+1,其中a、b是常数,等式右边是通常的加法和乘法运算.若3*5=15,4*7=28,则1*1=_________.
16.设α、β表示平面,l表示不在α内也不在β内的直线,存在下列三个事实:
①l⊥α;②l∥β;③α⊥β,若以其中两个作为条件,另一个作为结论,可构成三个命题,其中真命题是_________.(要求写出所有真命题)
高考数学客观题限时训练一 班级 姓名 学号 记分 参考答案
参考答案
训练一
1-4 CBCA 5-8 DCCA 9-10 DC
11、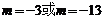 12、135
13、
12、135
13、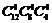 14、
14、 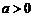 15
15
15、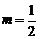 16、①②
16、①②
训练二
1.D 2.C 3.A 4.C 5.B 6.B 7.A 8.A 9.D 10.B 11.B 12.D
13.(-1,-1) 14.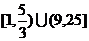 .
.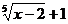
训练三、
|
答案 |
D |
C |
B |
C |
D |
B |
C |
A |
C |
C |
A |
A |
13. 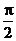 ; 14.
; 14. 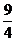 ;
15. ① ② ④
; 16.
;
15. ① ② ④
; 16. 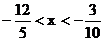 ;
;
训练四、
一.选择题:BCBBD BCCCA BB
二.填空题:13. 14.(
14.(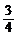 ,+∞) 15.
,+∞) 15.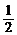 16.2
16.2
训练五、
1.B 2.A 3.B 4.B 5.C 6.B 7.B 8.A 9.C 10.B 11.C 12.B
二、填空题答案:
13.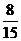 14.分层抽取;4 15.56 16.
14.分层抽取;4 15.56 16.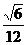
训练六
一、选择题
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
答案 |
C |
B |
A |
B |
A |
D |
D |
B |
D |
C |
A |
D |
二、填空题
13.43 14.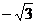 15.2004 16.②④
15.2004 16.②④
训练七
CABBCBDCDAAD
(13..)
35 (14) 2 (15) [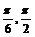 ]
( 16). 1679
]
( 16). 1679
训练8
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
答案 |
A |
C |
B |
B |
B |
B |
A |
A |
C |
A |
D |
C |
二、 填空题:(本大题共4小题,每小题4分,共16分,把答案填在题目中的横线上。)
13.  14. 12 15. ___16__
16.
14. 12 15. ___16__
16.
训练九
一、1、B 2、C 3、D 4、B 5、A 6、C 7、C 8、A 9、A 10、D
11、A 12、D
二、13、9π 14、9 15、42 16、①④
客观题限时训练十
一、选择题:(每题5分,共60分)
1.D 2. A 3.C 4.B 5.C 6.C 7.C 8.D 9.D 10.A 11.B 12.B
二、填空题:(每题4分,共16分)
13.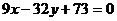 14.
14.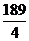 15.
15. 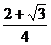 16.
16.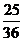
客观题限时训练十一
ADCBD,DCBAC;BA
13.60° 14.x=2 15.-11 16.①②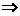 ③,①③
③,①③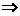 ②
②