1．(人教A版选修2-3第22页例4)

用 0 到 9 这 10 个数字，可以组成多少个没有重复数字的三位数 ？

变式1： 由1，4，5，x可组成没有重复数字的四位数，若所有这些四位数的各位数字之和为288，则x＝　　　　　　 　．

[解析]：(1+4+5+x)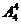=288，解得10+x=12．

[答案]：x=2．

变式2：在由数字1，2，3，4，5组成的所有没有重复数字的5位数中，大于23145且小于43521的数共有 (　　 )

(A)56个　　　(B)57个　　(C)58个　　(D)60个

[解答]解法一：(直接法)

当首位排2，次位排3时，有A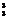-1种；次位排4、5时有2 A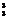种，共计17种；

当首位排3，A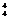种，共计24种；

当首位排4，次位排3时，有A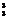-1种；次位排1、2时有2 A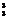种，共计17种；

以上总计17+24+17=58种。

解法二：(间接法)

不作限定时有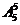=120种；

当首位排1或5时，各有A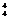种，共计48种不满足要求；

当首位排2，次位排1时，有A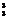种；而次位排3时有1种，共计7种不满足要求；

当首位排4，次位排5时，有A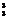种；而次位排3时有1种，共计7种不满足要求；

因此共有120-48-7-7=58种排法，即58个数．

变式3：给定数字0、1、2、3、5、9每个数字最多用一次

(1)可能组成多少个四位数？

(2)可能组成多少个四位奇数？

(3)可能组成多少个四位偶数？

(4)可能组成多少个自然数？

[分析]：注意0不能放在首位，还要注意个位数字，方法多种多样，利用特殊优先法，即特殊的元素，特殊的位置优先考虑．

[解答](1)解法一：从“位置”考虑，由于0不能放在首位，因此首位数字只能有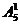种取法，其余3个数位可以从余下的5个数字(包括0)中任取3个排列，所以可以组成个四位数；

解法二：从“元素”考虑，组成的四位数可以按有无数字0分成两类，有数字0的有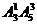个，无数字0的有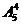个，所以共组成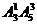+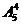=300个四位数；

解法三：“排除法”从6个元素中取4个元素的所有排列中，减去0在首位上的排列数即为所求，所以共有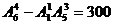个四位数；

(2)从“位置”考虑，个位数字必须是奇数有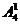种排法，由于0不能放在首位，因此首位数字只能有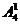种取法，其余两个数位的排法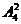有，所以共有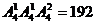个四位奇数；

(3)解法一：由(1)(2)知共有300-192=108个四位偶数；

解法二：从“位置”考虑，按个位数字是否为0分成两种情况，0在个位时，有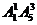个四位偶数；2在个位时，有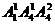个四位偶数，所以共有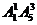+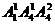=108个四位偶数；

(4)一位数：有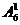=6个；

两位数：有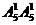=25个；

三位数：有=100个；

四位数：有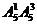=300个；

五位数：有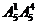=600个；

六位数：有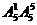=600个；

所以共有6+25+100+300+600+600=1631个自然数．

[点评]解有条件限制的排列问题思路：①正确选择原理；②处理好特殊元素和特殊位置，先让特殊元素占位，或特殊位置选元素；③再考虑其余元素或其余位置；④数字的排列问题，0不能排在首位．

2．(人教A版选修2-3第29页例4)

在 100 件产品中，有 98 件合格品，2 件次品，从这 100 件产品中任意抽出 3 件。

(1)有多少种不同的抽法 ？

(2)抽出的 3 件中恰好有 1 件是次品的抽法有多少种 ？

(3)抽出的 3 件中至少有 1 件是次品的抽法有多少种 ？

变式1：某人手中有5张扑克牌，其中2张为不同花色的2，3张为不同花色的A，有5次出牌机会，每次只能出一种点数的牌但张数不限，此人有多少种不同的出牌方法？

[分析]：分类讨论，由于情况太多，要做到不重不漏．

[解答]出牌的方法可分为以下几类：

(1)5张牌全部分开出，有种方法；　　

(2)2张2一起出，3张A一起出，有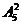种方法；　　

(3)2张2一起出，3张A分开出，有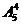种方法；　　

(4)2张2一起出，3张A分两次出，有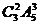种方法；　

(5)2张2分开出，3张A一起出，有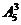种方法；　　

(6)2张2分开出，3张A分两次出，有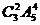种方法；

因此，共有不同的出牌方法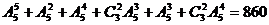种．

[点评]分类讨论一直是高中的难点，但更是高考的热点内容之一，所以同学们不能回避，应加强训练．

变式2：将7个小球任意放入四个不同的盒子中，每个盒子都不空，

　 (1)若7个小球相同，共有多少种不同的放法？

　 (2)若7个小球互不相同，共有多少种不同的放法？

[解析]：(1)解法1：∵7=1+1+1+4=1+1+2+3=1+2+2+2，

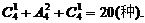∴分三类，共有分法

解法2(隔板法)：将7个小球排成一排，插入3块隔板，

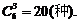故共有分法

　 (2)∵7=1+1+1+4=1+1+2+3=1+2+2+2，

∴共有分法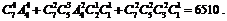

变式3：一个口袋内有4个不同的红球，6个不同的白球，

　 (1)从中任取4个球，红球的个数不比白球少的取法有多少种？

　 (2)若取一个红球记2分，取一个白球记1分，从中任取5个球，使总分不少于7分的

取法有多少种？

[解析]：(1)将取出4个球分成三类情况1)取4个红球，没有白球，有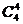种　 2)取3个红球1个白球，有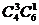种；3)取2个红球2个白球，有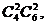

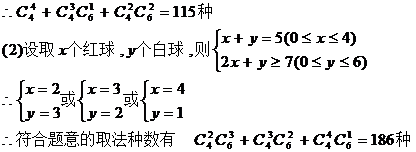
3．(人教A版选修2-3第36页例2)

(1)求 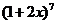　的展开式的第 4 项的系数 ；

(2)求 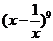　的展开式中 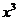　的系数 ？

变式1：在二项式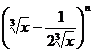的展开式中，前三项系数的绝对值成等差数列．

(1)求展开式的第四项；

(2)求展开式的常数项；

(3)求展开式的各项系数的和．

[分析]：本题旨在训练二项式定理通项公式的运用．

[解答]第一项系数的绝对值为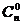，第二项系数的绝对值为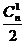，第三项系数的绝对值为，

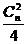依题意有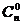+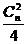=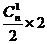，解得n=8，

(1)第四项；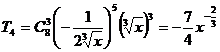

(2)通项公式为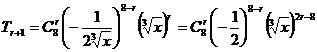，展开式的常数项有2r-8=0，即r=4，

常数项为；

(3)令x=1，得展开式的各项系数的和．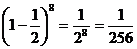

[点评]本题旨在训练二项式定理通项公式的运用，但要注意通项为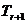而不是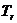，这是同学们最容易出错的地方．

变式2：设．

(1)求；

(2)求；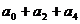

(3)求；

(4)求；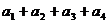

(5)求各项二项式系数的和．

[分析]：本题旨在训练二项展开式各项的系数与二项式系数．

[解答](1)令x=1得；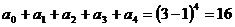

(2)令x=-1得，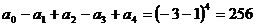

而由(1)知：，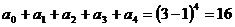

两式相加得；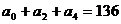

(3)将(2)中的两式相减得；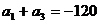

(4)令x=0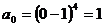得，得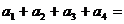-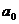=16-1=15；

(5)各项二项式系数的和为．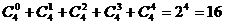

[点评]①要注意二项展开式各项的系数与二项式系数是不同的两个概念；②系数和与二项式系数和不一定相同，本题的(1)与(5)结果相同纯属巧合；③注意求系数和上述是最一般的方法，一定要理解．

变式3：二项展开式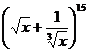中，有理项的项数是(　　 )

(A) 3

(B) 4

(C) 5

(D) 6

[解析]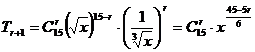：(r = 0，1，2，…，14 )，

当r = 3，9，15时，为有理项．

[答案]：A

变式4： 若，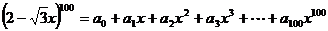

求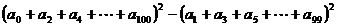的值．

[解析]：令x=1得，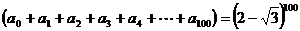

令x=-1得

=

=

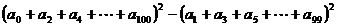
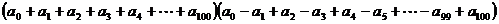
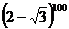
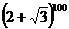
=1

[答案]：1