
例2、
已知数列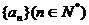 满足:
满足: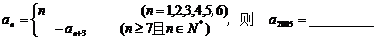 。
。
解:由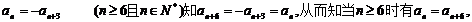 于是知
于是知
 。
。
评析:本题主要通过对数列形式的挖掘得出数列特有的性质,从而达到化归转化解决问题的目的。其中性质探求是关键。
例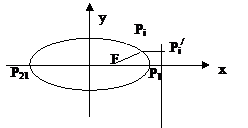 3、设F是椭圆
3、设F是椭圆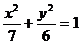 的右焦点,且椭圆上至少有21个不同的点Pi(i=1,2,3,…),使|FP1|,|FP2|,|FP3|,…组成公差为d的等差数列,则d的取值范围为
.
的右焦点,且椭圆上至少有21个不同的点Pi(i=1,2,3,…),使|FP1|,|FP2|,|FP3|,…组成公差为d的等差数列,则d的取值范围为
.
解析:由椭圆第二定义知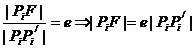 ,这些线段长度的最小值为右焦点到右顶点的距离即|FP1|=
,这些线段长度的最小值为右焦点到右顶点的距离即|FP1|=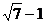 ,最大值为右焦点到左顶点的距离即|FP21|=
,最大值为右焦点到左顶点的距离即|FP21|=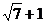 ,故若公差d>0,则
,故若公差d>0,则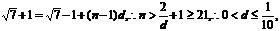 同理若公差d<0,则可求得
同理若公差d<0,则可求得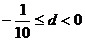 。
。
评析:本题很好地将数列与椭圆的有关性质结合在一起,形式新颖,内容深遂,有一定的难度,可见命题设计者的良苦用心。解决的关键是确定该数列的最大项、最小项,然后根据数列的通项公求出公差的取值范围。
例4、
若数列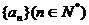 是等差数列,则有数列
是等差数列,则有数列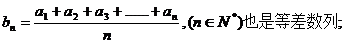 类比上述性质,相应地:若数列
类比上述性质,相应地:若数列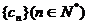 是等比数列,且
是等比数列,且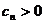 ,则有数列
,则有数列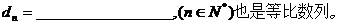
解析:由已知“等差数列前n项的算术平均值是等差数列”可类比联想“等比数列前n项的几何平均值也应该是等比数列”不难得到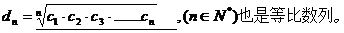
评析:本题只须由已知条件的特征从形式和结构上对比猜想不难挖掘问题的突破口。
例5、将自然数不清,2,3,4……排成数陈(如右图),在2处转第一个弯,在3转第二个弯,在5转第三个弯,….,则第2005个转弯处的数为____________。
解:观察由1起每一个转弯时递增的数字可发现为“1,1,2,2,3,3,4,4,……”。故在第2005个转弯处的数为:
1+2(1+2+3+……+1002)+1003=1006010。
评析:本题求解的关键是对图表转弯处数字特征规律的发现。具体解题时需要较强的观察能力及快速探求规律的能力。因此,它在高考中具有较强的选拔功能。
例6、下表给出一个“等差数阵”:
|
4 |
7 |
(
) |
(
) |
(
) |
…… |
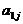 |
…… |
|
7 |
12 |
(
) |
(
) |
(
) |
…… |
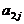 |
…… |
|
(
) |
(
) |
(
) |
(
) |
(
) |
…… |
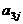 |
…… |
|
(
) |
(
) |
(
) |
(
) |
(
) |
…… |
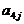 |
…… |
|
…… |
…… |
…… |
…… |
…… |
…… |
…… |
…… |
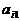 |
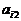 |
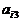 |
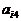 |
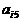 |
…… |
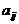 |
…… |
|
…… |
…… |
…… |
…… |
…… |
…… |
…… |
…… |
其中每行、每列都是等差数列,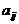 表示位于第i行第j列的数。
表示位于第i行第j列的数。
(I)写出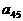 的值;(II)写出
的值;(II)写出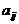 的计算公式;
的计算公式;
(III)证明:正整数N在该等差数列阵中的充要条件是2N+1可以分解成两个不是1的正整数之积。
解:(I)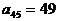 (详见第二问一般性结论)。
(详见第二问一般性结论)。
(II)该等差数阵的第一行是首项为4,公差为3的等差数列: 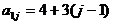 ; 第二行是首项为7,公差为5的等差数列:
; 第二行是首项为7,公差为5的等差数列: 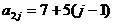 , ……,第i行是首项为
, ……,第i行是首项为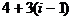 ,公差为
,公差为 的等差数列,因此
的等差数列,因此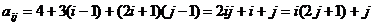
(III)必要性:若N在该等差数阵中,则存在正整数i,j使得 ,从而
,从而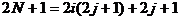
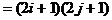 。
即正整数2N+1可以分解成两个不是1的正整数之积。
。
即正整数2N+1可以分解成两个不是1的正整数之积。
充分性:若2N+1可以分解成两个不是1的正整数之积,由于2N+1是奇数,则它必为两个不是1的奇数之积,即存在正整数k,l,使得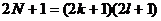 , 从而
, 从而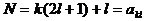 可见N在该等差数阵中。
可见N在该等差数阵中。
综上所述,正整数N在该等差数阵中的充要条件是2N+1可以分解成两个不是1的正整数之积。
评析: 本小题主要考查等差数列、充要条件等基本知识,考查逻辑思维能力、分析问题和解决问题的能力。求解关键是如何根据图表信息求出行列式中对应项的通项公式。
例7、如图,第n个图形由第n+2边形“扩展”而来的。记第n个图形的顶点数为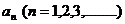 ,则
,则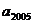 = 。
= 。
解:由图易知: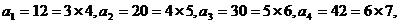 从而易知
从而易知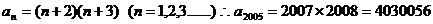
评析:求解几何计数问题通常采用“归纳-猜想-证明”解题思路。本题也可直接求解。第n个图形由第n+2边形“扩展”而来的,这个图形共由n+3个n+2边形组成,而每个n+2边形共有n+2个顶点,故第n个图形的顶点数为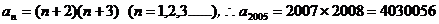 。
。
例8、如图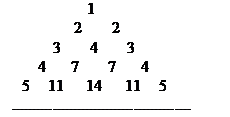 是一个类似“杨辉三角”的图形,第n行共有n个数,且该行的第一个数和最后一个数都是n,中间任意一个数都等于第n-1行与之相邻的两个数的和,
是一个类似“杨辉三角”的图形,第n行共有n个数,且该行的第一个数和最后一个数都是n,中间任意一个数都等于第n-1行与之相邻的两个数的和, 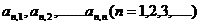 分别表示第n行的第一个数,第二个数,…….第n 个数。
分别表示第n行的第一个数,第二个数,…….第n 个数。
求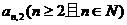 的通项式。
的通项式。
解:(1)由图易知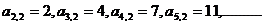 从而知
从而知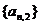 是一阶等差数列,即
是一阶等差数列,即
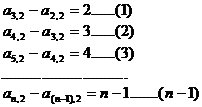
以上n-1个式相加即可得到:
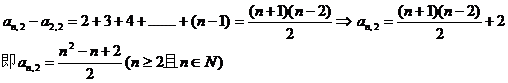
评析:“杨辉三角”型数列创新题是近年高考创新题的热点问题。求解这类题目的关键是仔细观察各行项与行列式的对应关系,通常需转化成一阶(或二阶)等差数列结合求和方法来求解。有兴趣的同学不妨求出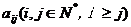 的通项式。
的通项式。