
1.函数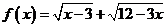 的值域为( )
的值域为( )
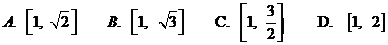
解: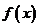 的定义域为
的定义域为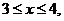 则
则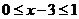 ,令
,令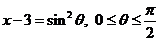 ,则
,则
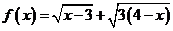

因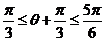 ,则
,则 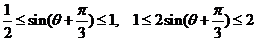 .
.
故选D
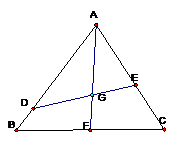
2.如图,已知△ABC是边长为1的正三角形,点D、E分别是边AB、AC上的点,线段DE经过△ABC的中心G, ,
,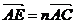 (0<m
(0<m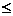 1,0<n
1,0<n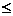 1)。
1)。
 (1)求证:
(1)求证: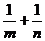 =3
=3
(2)求△ADE的面积的最小值和最大值。
解:(1)如图延长AG交BC与F,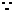 G为△ABC的中心
G为△ABC的中心
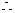 F为BC的中点,则有
F为BC的中点,则有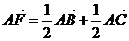
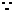
 ,
,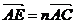 ,
,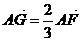
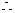
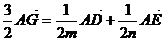 即
即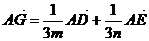
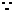 D、G、E三点共线
D、G、E三点共线
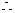
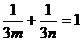 故
故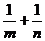 =3
=3
(2)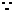 △ABC是边长为1的正三角形
△ABC是边长为1的正三角形
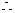
 ,
,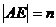
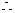 S
S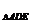 =
=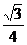 mn
mn
由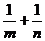 =3,0<m
=3,0<m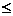 1,0<n
1,0<n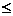 1
1
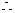 n=
n=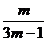 ,
,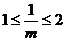 即
即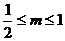 。
。
 S
S =
=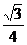 mn=
mn=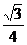

设t=m-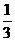 则m=t+
则m=t+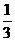 (
(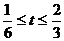 )
)
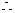 S
S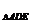 =
=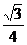 mn=
mn=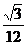 (t+
(t+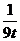 +
+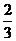 )
)
易知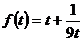 在
在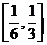 为减函数,在
为减函数,在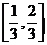 为增函数。
为增函数。
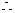 t=
t=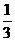 时,
时,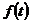 取得最小值
取得最小值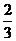 ,即S
,即S 取得最小值
取得最小值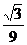
又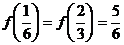 ,
,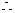
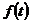 取得最大值是
取得最大值是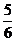 ,则S
,则S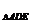 取得最大值
取得最大值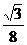
3.若集合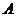 中的每个元素都可表为
中的每个元素都可表为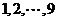 中两个不同的数之积,则集
中两个不同的数之积,则集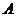 中元素个数的最大值为
.
中元素个数的最大值为
.
解:从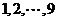 中每次取一对作乘积,共得
中每次取一对作乘积,共得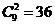 个值,但其中有重复,重复的情况为
个值,但其中有重复,重复的情况为  ,共
,共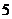 种,因此集合
种,因此集合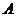 中至多有
中至多有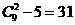 个数。故答:
个数。故答: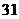 .
.
4.在数列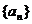 中,
中,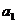 =2,
=2,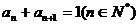 ,设
,设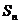 为数列
为数列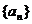 的前n项和,则
的前n项和,则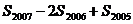 的值为
的值为
解:法-
当n为偶数时,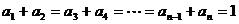 ,故
,故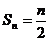
当n奇数时,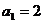 ,
,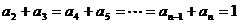 ,故
,故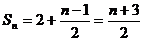
故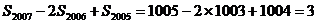
法二
由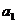 =2,
=2,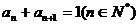 ,可得an=
,可得an=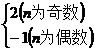
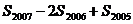 =S2007-S2006-(S2006-S2005)=a2007-a2006=2-(-1)=3
=S2007-S2006-(S2006-S2005)=a2007-a2006=2-(-1)=3
5.已知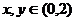 ,且xy=1,则
,且xy=1,则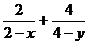 的最小值是 ( )
的最小值是 ( )
A、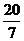 B、
B、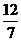 C、
C、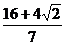 D、
D、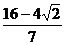
解:由已知得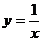 ,所以
,所以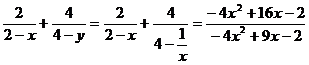
=
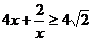 当且仅当
当且仅当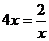 ,即
,即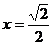 时,取等号
时,取等号
故当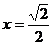 时,
时,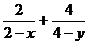 有最小值
有最小值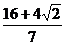
6.数列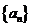 定义如下:
定义如下: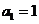 ,且当
,且当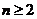 时,
时,
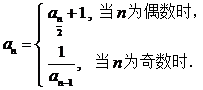
已知an=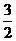 ,则正整数n=
。
,则正整数n=
。
解:由题设易知,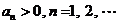 .又由
.又由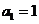 ,可得,当n为偶数时,
,可得,当n为偶数时,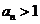 ;当
;当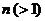 是奇数时,
是奇数时,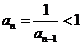 .
.
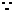 an=
an=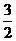 >1
>1 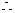 n为偶数,an=
n为偶数,an=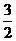 =
=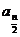 +1
+1
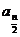 =
=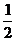 <1
<1 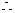
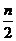 为奇数,
为奇数,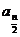 =
=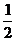 =
=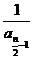
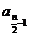 =2>1
=2>1 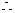
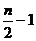 为偶数,
为偶数,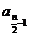 =2=
=2=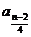 +1
+1
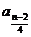 =1
=1 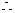
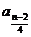 =a1
=a1
故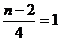 即n=6
即n=6
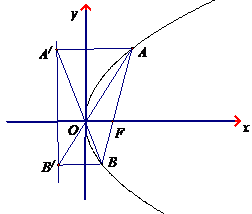
7.已知抛物线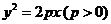 ,其焦点为F,一条过焦点F,倾斜角为
,其焦点为F,一条过焦点F,倾斜角为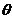
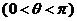 的直线交抛物线于A,B两点,连接AO(O为坐标原点),交准线于点
的直线交抛物线于A,B两点,连接AO(O为坐标原点),交准线于点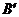 ,连接BO,交准线于点
,连接BO,交准线于点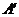 ,求四边形
,求四边形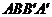 的面积.
的面积.
解 当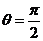 时,
时,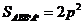 .
.
 当
当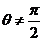 时,令
时,令 .设
.设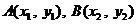 ,则由
,则由
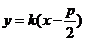 , ①
, ①
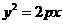 ,
②
,
②
消去x得,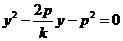 ,所以
,所以
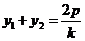 ,
, 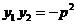 . ③
. ③
又直线AO的方程为: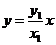 ,即为
,即为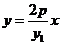 ,所以,AO与准线的交点的坐标为
,所以,AO与准线的交点的坐标为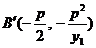 ,而由③知,
,而由③知,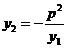 ,所以B和
,所以B和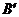 的纵坐标相等,从而
的纵坐标相等,从而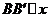 轴.同理
轴.同理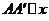 轴,故四边形
轴,故四边形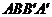 是直角梯形
是直角梯形
所以,它的面积为
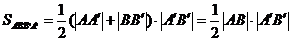
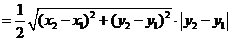
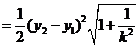
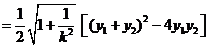
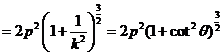 .
.