
1.在等比数列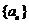 中,
中,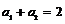 ,
,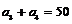 ,则公比
,则公比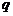 的值为 ( )
的值为 ( )
A.25 B.5 C.-5 D.±5
2.已知等差数列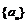 中,
中,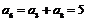 ,则
,则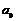 的值是
( )
的值是
( )
A.5 B. 15 C.20 D.25
3.给定正数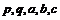 ,其中
,其中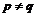 ,若
,若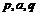 成等比数列,
成等比数列,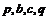 成等差数列,则一元二次方程
成等差数列,则一元二次方程
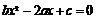 ( )
( )
A.无实数根 B.有两个相等的实数根
C.有两个同号的相异的实数根 D.有两个异号的相异的实数根
4.等差数列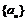 的前
的前 项和记为
项和记为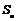 ,若
,若 为一个确定的常数,则下列各数中也是常数的是(
)
为一个确定的常数,则下列各数中也是常数的是(
)
A.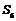 B.
B.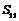 C.
C.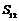 D.
D.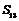
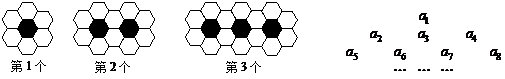
5.设数列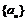 为等差数列,且
为等差数列,且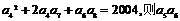 等于
(
)
等于
(
)
A.501 B.±501 C.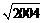 D.±
D.±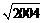
6.已知等差数列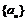 的前
的前 项和为
项和为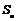 ,若
,若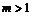 ,且
,且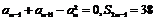 ,则
,则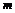 等于(
)
等于(
)
A.38 B.20 C.10 D.9
7.设等比数列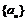 的前
的前 项和为
项和为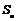 ,若
,若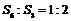 ,则
,则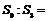 (
)
(
)
A.1:2 B.2:3 C.3:4 D.1:3
8.某人为了观看2008年奥运会,从2001年起,每年5月10日到银行存入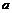 元定期储蓄,若年利率为
元定期储蓄,若年利率为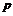 且保持不变,并约定每年到期存款均自动转为新的一年定期,到2008年将所有的存款及利息全部取回,则可取回的钱的总数(元)为
( )
且保持不变,并约定每年到期存款均自动转为新的一年定期,到2008年将所有的存款及利息全部取回,则可取回的钱的总数(元)为
( )
A.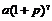 B.
B.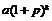
C.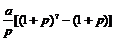 D.
D.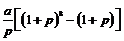
9.已知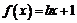 为
为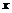 的一次函数,
的一次函数,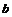 为不等于1的常量,且
为不等于1的常量,且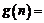
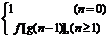 ,
设
,
设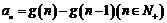 ,则数列
,则数列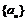 为 ( )
为 ( )
A.等差数列 B.等比数列 C.递增数列 D.递减数列
10.已知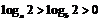 ,则
,则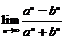 的值为
( )
的值为
( )
A.1 B.-1 C.0 D.不存在
11.北京市为成功举办2008年奥运会,决定从2003年到2007年5年间更新市内现有全部出租车,若每年更新的车辆数比前一年递增10%,则2003年底更新车辆数约为现有总车辆数的(参考数据1.14=1.46 1.15=1.61) ( )
A.10% B.16.4% C.16.8% D.20%
12.已知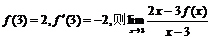 的值为 ( )
的值为 ( )
A.-4 B.8 C.0 D.不存在
13.已知等比数列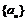 及等差数列
及等差数列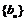 ,其中
,其中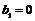 ,公差
,公差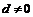 .将这两个数列的对应项相加,得一新数列1,1,2,…,则这个新数列的前10项之和为
.
.将这两个数列的对应项相加,得一新数列1,1,2,…,则这个新数列的前10项之和为
.
14.设数列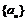 满足
满足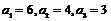 ,且数列
,且数列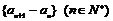 是等差数列,求数列
是等差数列,求数列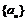 的通项公式
.
的通项公式
.
15.设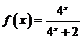 ,利用课本中推导等差数列前
,利用课本中推导等差数列前 项和方法,求
项和方法,求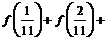 …
…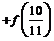 的值为
.
的值为
.
16.(文)黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案:
则第 个图案中有白色地面砖
块.
个图案中有白色地面砖
块.
(理)已知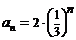 ,把数列
,把数列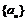 的各项排成三角形状;
的各项排成三角形状;
记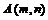 表示第
表示第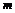 行,第
行,第 列的项,则
列的项,则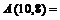 .
.
17.(本小题满分12分)已知一个数列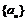 的各项是1或3.首项为1,且在第
的各项是1或3.首项为1,且在第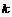 个1和第
个1和第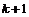 个1之间有
个1之间有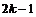 个3,即1,3,1,3,3,3,1,3,3,3,3,3,1,….记数列的前
个3,即1,3,1,3,3,3,1,3,3,3,3,3,1,….记数列的前 项的和为
项的和为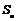 .
.
(1)试问第2004个1为该数列的第几项?(2)求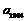 ;(3)
;(3)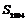 ;
;
(4)是否存在正整数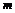 ,使得
,使得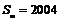 ?如果存在,求出
?如果存在,求出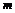 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
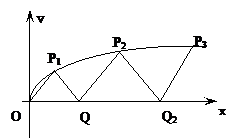
18.(本小题满分12分)如图,曲线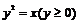 上的点
上的点 与
与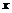 轴的正半轴上的点
轴的正半轴上的点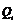 及原点
及原点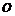 构成一系列正三角形△
构成一系列正三角形△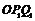 ,△
,△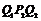 ,…△
,…△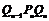 …设正三角形
…设正三角形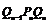 的边长为
的边长为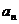 ,
,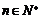 (记
(记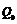 为
为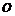 ),
),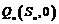 .
.
 (1)求
(1)求 的值;(2)求数列
的值;(2)求数列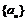 的通项公式
的通项公式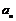 ;
;
(3)求证:当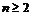 时, 有
时, 有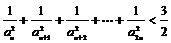 .
.
19.(本小题满分12分)假设你正在某公司打工,根据表现,老板给你两个加薪的方案:
(Ⅰ)每年年末加1000元; (Ⅱ)每半年结束时加300元。请你选择。
(1)如果在该公司干10年,问两种方案各加薪多少元?
(2)对于你而言,你会选择其中的哪一种?
20.(本小题满分12分)已知数列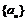 的前
的前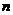 项的“均倒数”为
项的“均倒数”为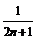 ,
,
(1)求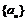 的通项公式;(2)设
的通项公式;(2)设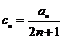 ,试判断并说明
,试判断并说明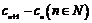 的符号;
的符号;
(3)(理)设函数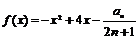 ,是否存在最大的实数
,是否存在最大的实数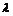 ,当
,当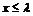 时,对于一切自然数
时,对于一切自然数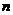 ,都有
,都有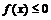 。
。
(文)已知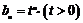 ,数列
,数列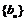 的前
的前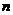 项为
项为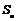 ,求
,求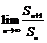 的值。
的值。
21.(本小题满分12分)若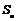 和
和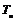 分别表示数列
分别表示数列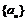 和
和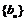 的前
的前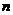 项和,对任意正整数
项和,对任意正整数
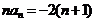 ,
,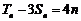 .
.
(Ⅰ)求数列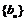 的通项公式;
的通项公式;
(Ⅱ)在平面直角坐标系内,直线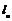 的斜率为
的斜率为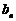 .且与曲线
.且与曲线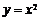 有且仅一个交点,与
有且仅一个交点,与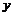 轴交于
轴交于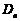 ,记
,记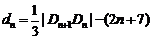 求
求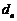 ;
;
(Ⅲ)若
22.(本小题满分14分)已知数列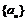 中,
中,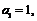 且点
且点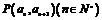 在直线
在直线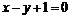 上.
上.
(1)求数列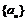 的通项公式;
的通项公式;
(2)若函数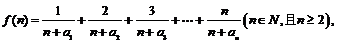 求函数
求函数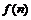 的最小值;
的最小值;
(3)设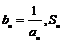 表示数列
表示数列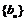 的前项和。试问:是否存在关于
的前项和。试问:是否存在关于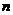 的整式
的整式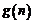 ,使得
,使得
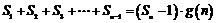 对于一切不小于2的自然数
对于一切不小于2的自然数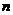 恒成立?若存在,写出
恒成立?若存在,写出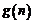 的解析式,并加以证明;若不存在,试说明理由。
的解析式,并加以证明;若不存在,试说明理由。
高考数学数列与极限专项训练(02)参考答案
参 考 答 案(二)
一、选择题(每小题5分,共60分):
(1).D (2). C (3).A (4).B (5). A (6). C (7).C (8). D (9).B (10).B (11). B (12).B
提示(9)B 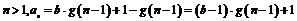
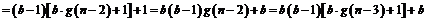
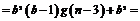 ……
……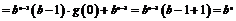
二、填空题(每小题4分,共16分)
(13). 978; (14). 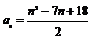 (n∈N*);(15).5;(16).(文)
(n∈N*);(15).5;(16).(文)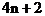 (理)
(理)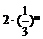
提示13.设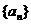 的公比为q,由题知:
的公比为q,由题知: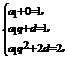 解得
解得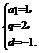 则
则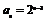 ,
,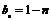 .这个新数列的前10项之和为
.这个新数列的前10项之和为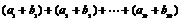
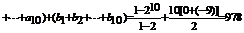
14. 由已知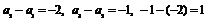 ∴
∴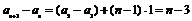
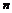 ≥2时,
≥2时,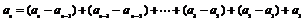
=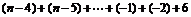 =
=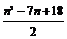
 也合适 ∴
也合适 ∴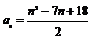
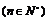
15. 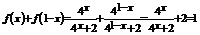
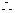 设
设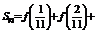 …
…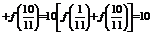
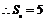
三、解答题(共74分,按步骤得分)
17. 解:将第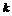 个1与第
个1与第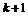 个1前的3记为第
个1前的3记为第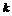 对,即(1,3)为第1对,共1+1=2项;(1,3,3,3)为第2对,共1+(2×2-1)=4项;
对,即(1,3)为第1对,共1+1=2项;(1,3,3,3)为第2对,共1+(2×2-1)=4项;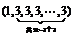 为第
为第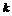 对,共
对,共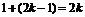 项;….故前
项;….故前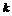 对共有项数为
对共有项数为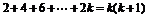 .
…………2分
.
…………2分
(Ⅰ)第2004个1所在的项为前2003对所在全部项的后1项,即为2003(2003+1)+1=4014013(项).…4分
(Ⅱ)因44×45=1980,45×46=2070,故第2004项在第45对内,从而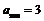 .…7分
.…7分
(Ⅲ)由(Ⅱ)可知,前2004项中共有45个1,其余1959个数均为3,于是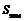 =45+3×1959=5922.…9分
=45+3×1959=5922.…9分
(Ⅳ)前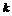 对所在全部项的和为
对所在全部项的和为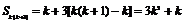 .
.
易得,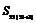 =3×252+25=1900,
=3×252+25=1900,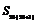 =3×262+26=2054,
=3×262+26=2054,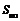 =1901,且自第652项到第702项均为3,而2004-1901=103不能被3整除,故不存在
=1901,且自第652项到第702项均为3,而2004-1901=103不能被3整除,故不存在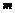 ,使
,使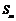 =2004.…………12分
=2004.…………12分
18. 解 (1)由条件可得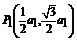 ,代入曲线
,代入曲线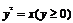 得
得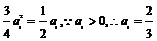 ;……5分
;……5分
(2) 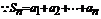 ∴点
∴点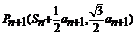 代入曲线
代入曲线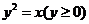 并整理得
并整理得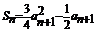 ,
,
于是当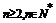 时,
时,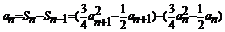 即
即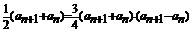
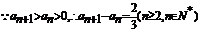 …………10分
…………10分
又当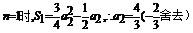
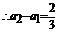 ,故
,故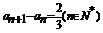
所以数列{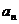 }是首项为
}是首项为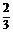 、公差为
、公差为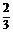 的等差数列,
的等差数列, 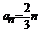 ;…………12分
;…………12分
19.解:设方案一第n年年末加薪an,因为每年末加薪1000元,则an=1000n;
设方案二第n个半年加薪bn,因为每半年加薪300元,则bn=300n;
(1)在该公司干10年(20个半年),方案1共加薪S10=a1+a2+……+a10=55000元。
方案2共加薪T20=b1+b2+……+b20=20×300+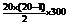 =63000元;……6分
=63000元;……6分
(2)设在该公司干n年,两种方案共加薪分别为:
Sn=a1+a2+……+an=1000×n+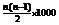 =500n2+500n
=500n2+500n
T2n=b1+b2+……+b2n=2n×300+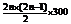 =600n2+300n …………10分
=600n2+300n …………10分
令T2n≥Sn即:600n2+300n>500n2+500n,解得:n≥2,当n=2时等号成立。
∴如果干3年以上(包括3年)应选择第二方案;如果只干2年,随便选;如果只干1年,当然选择第一方案…12分
20. 解:(1)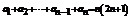 ,
,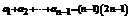 两式相减,得
两式相减,得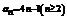 ,
,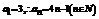
(2)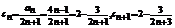 ,
,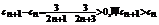 .…………8分
.…………8分
(3)(理)由(2)知 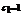 是数列
是数列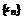 中的最小项,∵
中的最小项,∵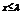 时,对于一切自然数
时,对于一切自然数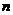 ,都有
,都有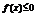 ,即
,即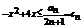 ,
,
∴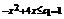 ,即
,即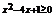 ,解之,得
,解之,得 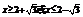 , ∴取
, ∴取 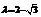 。 ……12分
。 ……12分
(文)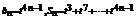 ,
,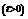 当
当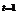 时,
时,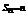 ,
,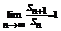 ;当
;当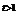 时,
时,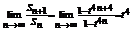 ;
;
当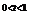 时,
时,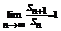 。综上得,
。综上得,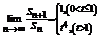 ………………12分
………………12分
21.解:(I)
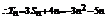 ……2分 当
……2分 当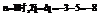
当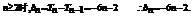 ……4分
……4分
(II)设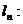
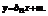 由
由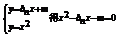 由于仅有一个公共点.
由于仅有一个公共点.
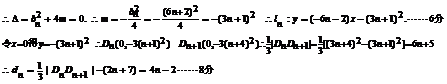
(III) …10分
…10分
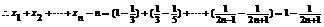
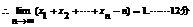
22.(本小题满分14分)
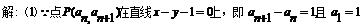

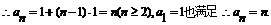 ………………3分
………………3分
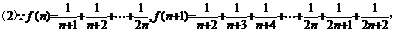
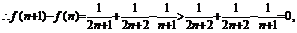 …6分
…6分
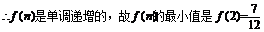 …12分
…12分
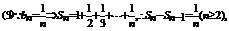
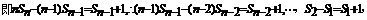
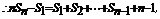
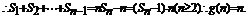 ……13分
……13分
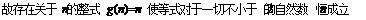 ……14分
……14分