
1.设集合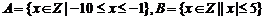 ,则
,则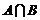 中元素的个数是
中元素的个数是
A.5 B.6 C.15 D.16
2.若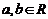 ,则使
,则使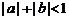 成立的一个充分不必要条件是
成立的一个充分不必要条件是
A.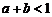 B.
B.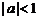 且
且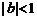
C.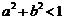 D.
D.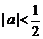 且
且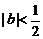
3.一个棱长为1的正方体的八个顶点都在同一个球面上,则此球的表面积为
A.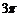 B.
B.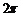 C.
C.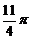 D.
D.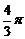
4.集合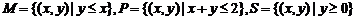 ,若
,若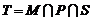 ,点
,点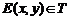 ,则
,则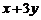 的最大值是
的最大值是
A.0 B.2 C.3 D.4
5.若向量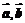 满足
满足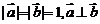 且
且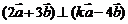 ,则实数k的值为
,则实数k的值为
A.-6 B.6 C.3 D.-3
6.已知a、b、c为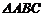 三内角A,B,C的对边,若
三内角A,B,C的对边,若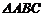 的面积为
的面积为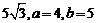 ,则c的值为
,则c的值为
A.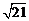 B.
B.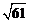 C.
C.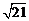 或
或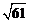 D.
D.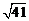
7.直线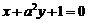 与
与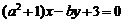 互相垂直,
互相垂直,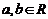 ,则
,则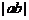 的最小
的最小
A.1 B.2 C.4 D.5
8.根据表格中的数据,可以判定方程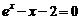 的一个根所在的区间为
的一个根所在的区间为
|
x |
-1 |
0 |
1 |
2 |
3 |
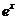 |
0.37 |
1 |
2.72 |
7.39 |
20.09 |
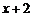 |
1 |
2 |
3 |
4 |
5 |
A.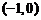 B.
B.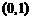 C.
C.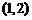 D.
D.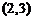
9.点P满足:到点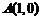 和直线
和直线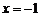 的距离相等,且到直线
的距离相等,且到直线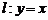 的距离为
的距离为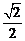 ,满足条件的点P的个数为
,满足条件的点P的个数为
A.1 B.2 C.3 D.4
10.正方体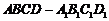 的校长为1,点M是棱AB上异于点A的一定点,点P是平面ABCD上的一动点,且点P到直线
的校长为1,点M是棱AB上异于点A的一定点,点P是平面ABCD上的一动点,且点P到直线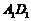 的距离两倍的平方比到点M的距离的平方大4,则点P的轨迹为
的距离两倍的平方比到点M的距离的平方大4,则点P的轨迹为
A.圆 B.椭圆 C.双曲线 D.抛物线
第Ⅱ卷(非选择题,共100分)
11.直线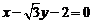 被圆
被圆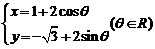 所截得的弦长为 ▲ .
所截得的弦长为 ▲ .
12.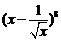 的展开式中x2的系数为
▲
.
的展开式中x2的系数为
▲
.
13.设函数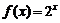 ,其反函数记为
,其反函数记为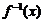 ,则函数
,则函数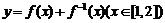 的值域
的值域
为 ▲ .
14.已知函数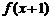 为奇函数,函数
为奇函数,函数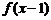 为偶函数,且
为偶函数,且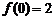 ,则
,则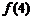 =
▲
=
▲
15.甲乙两人投篮中的概率分别为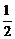 、
、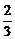 ,现两人各投两次,则投中总数为2的概率为
,现两人各投两次,则投中总数为2的概率为
▲ .
16.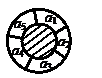 一个同心圆形花坛,分为两部分,如右图,中间小圆部分种
一个同心圆形花坛,分为两部分,如右图,中间小圆部分种
植草坪,周围的圆环分5等份为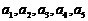 ,种植红、黄、蓝
,种植红、黄、蓝
三色不同的花,要求相邻两部分种植不同颜色的花,则不同的种
植方法种数为 ▲ .
17.(本小题满分12分)
已知函数 最小正周期为
最小正周期为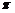 。
。
(1)求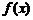 在区间
在区间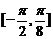 上的最小值;
上的最小值;
(2)求函数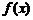 图象上与坐株原点最近的对称中心的坐标。
图象上与坐株原点最近的对称中心的坐标。
18..(本小题满分15分)
如图,已知四棱柱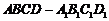 的底面ABCD为直角梯形,
的底面ABCD为直角梯形,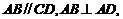 ,
,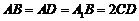 ,侧面
,侧面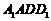 为正方形。
为正方形。
(1)求直线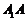 与底面ABCD所成角的大小;
与底面ABCD所成角的大小;
(2)求二面角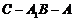 正切值的大小;
正切值的大小;
 (3)在棱
(3)在棱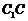 上是否存在一点P,使得
上是否存在一点P,使得 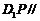 平面
平面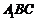 ,若存在,试说明点P的位置;若不存在,请说明理由.
,若存在,试说明点P的位置;若不存在,请说明理由.
19.(本小题满分14分)
数列 的前n项和为
的前n项和为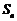 ,且满足
,且满足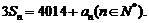
(1)求数列 的通项公式;
的通项公式;
(2)设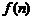 表示该数列的前n项的积,n取何值时,
表示该数列的前n项的积,n取何值时,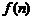 有最大值?
有最大值?
20.(本小题满分14分)
已知点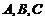 都在椭圆
都在椭圆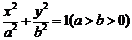 上,
上,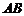 、AC分别过两个焦点
、AC分别过两个焦点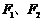 ,当
,当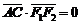 时,有
时,有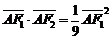 成立.
成立.
(1)求此椭圆的离心率;
(2)设 当点A在椭圆上运动时,求证
当点A在椭圆上运动时,求证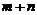 始终是定值.
始终是定值.
21.(本小题满分15分)
已知函数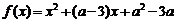 (a为常数).
(a为常数).
(1)如果对任意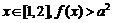 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(2)设实数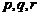 满足:
满足: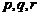 中的某一个数恰好等于a,且另两个恰为方程
中的某一个数恰好等于a,且另两个恰为方程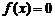 的两实根,判断①
的两实根,判断①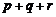 ,②
,②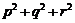 ,③
,③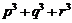 是否为定值?若是定值请求出:若不是定值,请把不是定值的表示为函数
是否为定值?若是定值请求出:若不是定值,请把不是定值的表示为函数 ,并求
,并求 的最小值;
的最小值;
(3)对于(2)中的 ,设
,设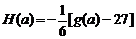 ,数列
,数列 满足
满足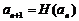
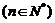 ,且
,且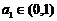 ,试判断
,试判断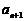 与
与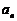 的大小,并证明.
的大小,并证明.