
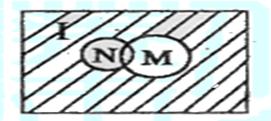
1. 设全集I是实数集R,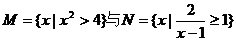 都是I的子集,则阴影部分(如图所示)所表示的集合为 ( )
都是I的子集,则阴影部分(如图所示)所表示的集合为 ( )
 A.
A.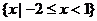 B.
B.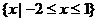
C.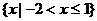 D.
D.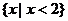
2、函数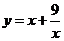 的单调递增区间为( )
的单调递增区间为( )
(A)(-3,3) (B)(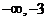 )(3,+
)(3,+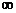 )(C)(-3,+
)(C)(-3,+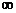 )(D)(-3,0),(0,3)
)(D)(-3,0),(0,3)
3、正四棱锥的一个对角面的面积是一个侧面面积的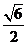 倍,则侧面与底面所成的角为(
)
倍,则侧面与底面所成的角为(
)
(A) 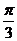 (B)
(B) 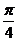 (C)
(C) 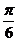 (D)
(D)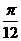
4、原点关于直线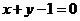 的对称点坐标为( )
的对称点坐标为( )
(A) (B)
(B)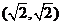 (C)
(C)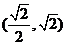 (D)(1,1)
(D)(1,1)
5、若D点在三角形ABC的BC边上,且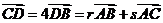 ,则
,则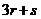 的值为( )
的值为( )
(A)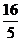 (B)
(B)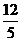 (C)
(C)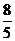 (D)
(D)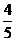
6、将一个各面均涂有油漆的正方体锯成1000个同样大小的小正方体,若将这些小正方体均匀地搅拌在一起,则任取一个小正方体,恰好是一个具有两面漆的正方体的概率是( )
(A) 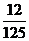 (B)
(B)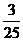 (C)
(C)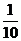 (D)
(D)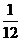
7、已知点A为双曲线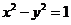 的顶点,点B和点C在双曲线的同一分支上,且A与B在y轴异侧,则正三角形ABC的面积是(
)
的顶点,点B和点C在双曲线的同一分支上,且A与B在y轴异侧,则正三角形ABC的面积是(
)
(A)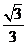 (B)
(B)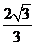 (C)
(C) (D)6
(D)6
8、给定性质:①最小正周期为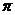 ,②图象关于直线
,②图象关于直线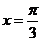 对称,则下列四个函数中,同时具有性质①②的是( )
对称,则下列四个函数中,同时具有性质①②的是( )
(A) 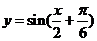 (B)
(B)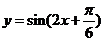 (C)
(C)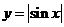 (D)
(D)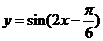
9、在等比数列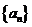 中
中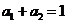 ,
,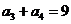 那么
那么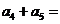 ( )
( )
(A)27 (B)-27 (C)81或-36 (D)27或-27
10、若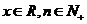 ,定义
,定义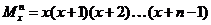 ,
,
列如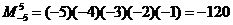 ,则函数
,则函数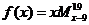 的奇偶性为( )
的奇偶性为( )
(A)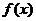 为偶函数,但不是奇函数
(B)
为偶函数,但不是奇函数
(B)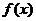 为奇函数,但不是偶函数
为奇函数,但不是偶函数
(C)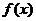 既是奇函数 ,又是偶函数
(D)
既是奇函数 ,又是偶函数
(D)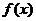 既不是奇函数,又不是偶函数
既不是奇函数,又不是偶函数
11.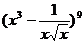 的展开式中的常数项是______.(用数字作答)
的展开式中的常数项是______.(用数字作答)
12.已知球的内接正方体的棱长为2,则该球的体积为 .
13.已知数列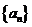 满足:
满足: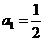 ,
,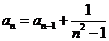
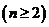 ,则
,则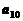 等于______
等于______
14.函数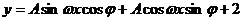
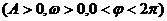 的图象如右,则
的图象如右,则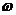 =______,
=______,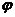 =______.
=______.
15.给出如下4个命题:①若α、β是两个不重合的平面,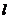 、m是两条不重合的直线,则α∥β的一个充分而不必要条件是
、m是两条不重合的直线,则α∥β的一个充分而不必要条件是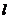 ⊥α,m⊥β,且
⊥α,m⊥β,且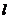 ∥m;②对于任意一条直线a,平面α内必有无数条直线与a垂直;③已知命题P:若四点不共面,那么这四点中任何三点都不共线.而命题P的逆否命题是假命题;④已知a、b、c、d是四条不重合的直线,如果a⊥c,a⊥d,b⊥c,b⊥d,则“a∥b”与“c∥d”不可能都不成立.在以上4个命题中,正确命题的序号是______. (要求将所有你认为正确的命题序号都填上)
∥m;②对于任意一条直线a,平面α内必有无数条直线与a垂直;③已知命题P:若四点不共面,那么这四点中任何三点都不共线.而命题P的逆否命题是假命题;④已知a、b、c、d是四条不重合的直线,如果a⊥c,a⊥d,b⊥c,b⊥d,则“a∥b”与“c∥d”不可能都不成立.在以上4个命题中,正确命题的序号是______. (要求将所有你认为正确的命题序号都填上)
16、
(本小题满分12分)已知数列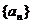 是等差数列,其前n项和为Sn,
是等差数列,其前n项和为Sn,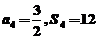 .
.
(1)求数列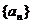 的通项公式;
的通项公式;
(2)求n取何值时,Sn最大,并求Sn的最大值.
17、
(本小题满分12分)在△ABC中,A,B,C是三角形的三内角,a,bc是三内角对应的三边,已知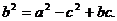
(1)求角A大小;
(2)若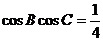 ,判断△ABC的形状.
,判断△ABC的形状.
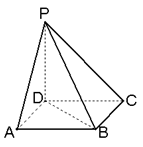
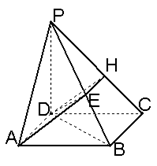
18、(本小题满分14分)如图,已知ABCD是正方形,PD⊥平面ABCD,PD=AD.
(1)求二面角A-PB-D的大小,
(2)在线段PB上是否存在一点E,使PC⊥平面ADE?若存在,确定E点的位置,若不存在,说明理由.
19、(本小题满分14分) 甲、乙两名射击运动员,甲射击一次命中10环的概率为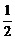 ,乙射击一次命中10环的概率为s。若他们各自独立地射击两次,乙至少有一次命中10环的概率为
,乙射击一次命中10环的概率为s。若他们各自独立地射击两次,乙至少有一次命中10环的概率为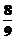 ,
,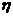 表示甲与乙命中10环的次数的差的绝对值。
表示甲与乙命中10环的次数的差的绝对值。
(1)求s的值;
(2)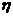 的所有可能值有哪些?
的所有可能值有哪些? 取这些值时的概率分别是多少?
取这些值时的概率分别是多少?
20、
(本小题满分14分)函数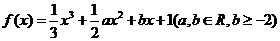 ,
,
当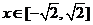 ,总有
,总有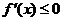 .
.
(1)求函数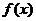 的解析式;
的解析式;
(2)设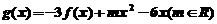 ,求证:当
,求证:当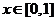 时,
时, 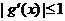 成立的充要条件是:
成立的充要条件是: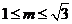
21、(本小题满分14分)已知点H(0,―3),点P在x轴上,点Q在y轴正半轴上,点M在直线PQ上,且满足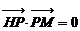 ,
,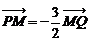 .
.
(1)当点P在x轴上移动时,求动点M的轨迹曲线C的方程; (2)过定点A(a,b)的直线与曲线C相交于两点S、R,求证:曲线C在S、R 两点处的切线的交点B恒在一条直线上.
(文科)1答案
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
B |
B |
A |
D |
C |
A |
C |
D |
D |
A |
16、解:(1)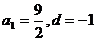 …………4分
…………4分
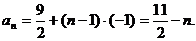 ………………6分
………………6分
(2)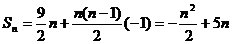 ………………9分
………………9分
当n=5时Sn取大值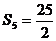 ………………12分
………………12分
17、解:(1)由已知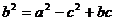 ,得
,得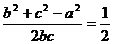
∴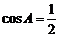 ,∴
,∴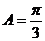 . …………6分
. …………6分
(2)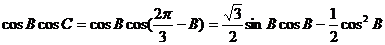

∴△ABC为等边三角形。 …………12分
18、(1)解法一:联结AC交DB于点O. ∵ABCD是正方形,∴AC⊥DB.
又PD⊥平面ABCD,AC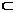 平面ABCD,
∴AC⊥PD, ∴AC⊥平面PBD.
平面ABCD,
∴AC⊥PD, ∴AC⊥平面PBD.
作OF⊥PB于点F,联结AF,则AF⊥PB.
∴∠OFA就是二面角A-PB-D的平面角. …………2分
∵PD⊥平面ABCD,AB⊥AD,∴PA⊥AB.
令PD=AD=2,则在RT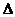 ABC中,PA=
ABC中,PA=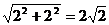 ,AB=2.
,AB=2.
∴PB=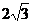 ,∴
,∴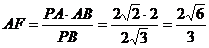 .
.
∴在RT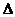 AOF中,sin
AOF中,sin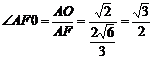 ,∴
,∴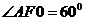 .
.
∴二面角A-PB-D的大小为 . …………7分
. …………7分
解法二:建立如图所示的直角坐标系.
联结AC,交BD于点O,取PA中点G,联结DG.
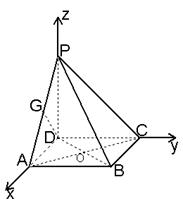 ∵ABCD是正方形,∴AC⊥DB.
∵ABCD是正方形,∴AC⊥DB.
又PD⊥平面ABCD,AC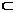 平面ABCD,
平面ABCD,
∴AC⊥PD, ∴AC⊥平面PBD.
∵PD⊥平面ABCD,AB⊥AD,∴PA⊥AB.
∴AB⊥平面PAD.
∵PD=AD,G为PA中点, ∴GD⊥平面PAB.
故向量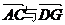 分别是平面PBD与平面PAB的法向量.
分别是平面PBD与平面PAB的法向量.
令PD=AD=2,则A(2,0,0),C(0,2,0),∴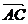 =(-2,2,0).
=(-2,2,0).
∵P(0,0,2),A(2,0,0), ∴G(1,0,1),∴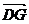 =(1,0,1). …………4分
=(1,0,1). …………4分
∴向量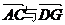 的夹角余弦为
的夹角余弦为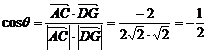 ,
,
∴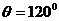 ,∴二面角A-PB-D的大小为
,∴二面角A-PB-D的大小为 . ………7分
. ………7分
 (2)解法一: 当点E是线段PB中点时,
(2)解法一: 当点E是线段PB中点时,
有PC⊥平面ADE. …7分
证明如下:
取PC中点H,联结EH,DH,则有EH∥BC,
又BC∥AD,故有EH∥AD.
∴平面ADE即平面ADHE. …………9分
∵PD=DC,H为PC中点, ∴PC⊥DH.
又∵PD⊥平面ABCD,AD⊥CD,∴AD⊥PC.
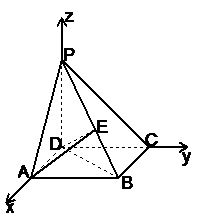 ∴PC⊥平面ADHE,即PC⊥平面ADE.
…………14分
∴PC⊥平面ADHE,即PC⊥平面ADE.
…………14分
解法二:建立如图所示的直角坐标系.
∵PD⊥平面ABCD,AD⊥CD,∴AD⊥PC.
设E是线段PB上的一点,令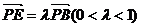 .
.
令PD=AD=2,则P(0,0,2),A(2,0,0),B(2,2,0),
C(0,2,0),
∴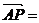 (-2,0,2),
(-2,0,2),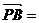 (2,2,-2),
(2,2,-2),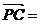 (0,2,-2).
(0,2,-2).
∴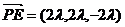 .
.
∴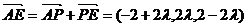 .
.
令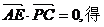 2
2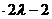 (
(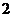 -
-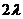 )=0,得
)=0,得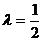 .
.
∴当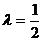 ,即点E是线段PB中点时,有AE⊥PC.
,即点E是线段PB中点时,有AE⊥PC.
又∵PD⊥平面ABCD,AD⊥CD,∴AD⊥PC.
∴当点E是线段PB中点时,有PC⊥平面ADE. …………14分
19、解:(1)依题意知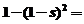
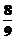 , ∴s=
, ∴s=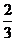 . ………3分
. ………3分
(2)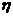 的取值可以是0,1,2.…………………………5分
的取值可以是0,1,2.…………………………5分
甲、乙两人命中10环的次数均为0次的概率是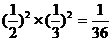 ,
,
甲、乙两人命中10环的次数均为1次的概率是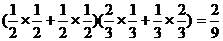 ,
,
甲、乙两人命中10环的次数均为2次的概率是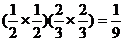 ,
,
∴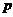 (
(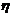 =0)=
=0)=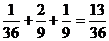 .
…………8分
.
…………8分
甲命中10环的次数为2次且乙命中10环的次数为0次的概率是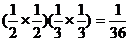 ,
,
甲命中10环的次数为0次且乙命中10环的次数为2次的概率是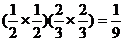 .∴
.∴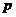 (
(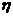 =2)=
=2)=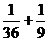 =
=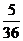 , ……11分
, ……11分
∴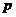 (
(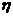 =1)=1
=1)=1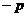 (
(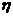 =0)
=0)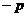 (
(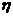 =2)=
=2)=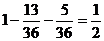 . ……14分
. ……14分
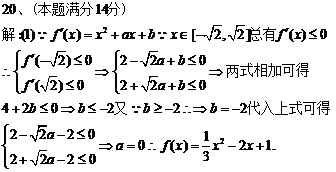
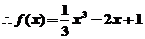

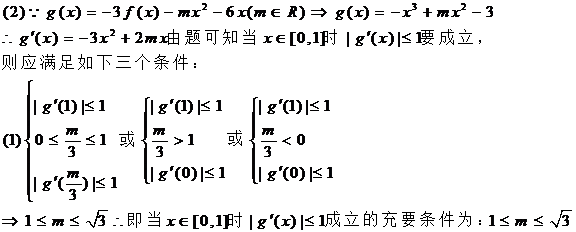
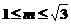
21、(1)解:设P(a,0),Q(0,b)则: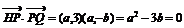 ∴
∴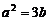 …………1分 设M(x,y)∵
…………1分 设M(x,y)∵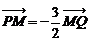 ∴
∴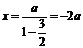
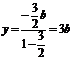 …4分 ∴点M的轨迹曲线C的方程是
…4分 ∴点M的轨迹曲线C的方程是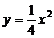 (x≠0) .6分
(x≠0) .6分
(2)解法一:设A(a,b),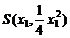 ,
,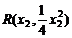 (x1≠x2)
(x1≠x2)
则:直线SR的方程为: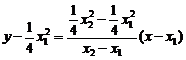 ,即4y = (x1+x2)x-x1x2 ∵A点在SR上,∴4b=(x1+x2)a-x1x2 ①
…………8分
,即4y = (x1+x2)x-x1x2 ∵A点在SR上,∴4b=(x1+x2)a-x1x2 ①
…………8分
对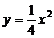 求导得:y′=
求导得:y′=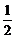 x∴抛物线上S、R处的切线方程为:
x∴抛物线上S、R处的切线方程为:
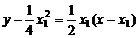 即4
即4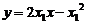 ②
②
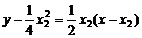 即4
即4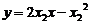 ③ …………11分
③ …………11分
联立②③,并解之得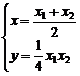 ,代入①得:ax-2y-2b=0
,代入①得:ax-2y-2b=0
故B点恒在直线ax-2y-2b=0上. …………14分
解法二:设A(a,b)
当过点A的直线斜率不存在时l与抛物线有且仅有一个公共点,与题意不符,可设直线SR的方程为y-b=k(x-a)与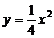 联立消去y得:x2-4kx+4ak-4b=0 …8分
设
联立消去y得:x2-4kx+4ak-4b=0 …8分
设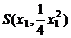 ,
,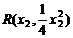 (x1≠x2)
(x1≠x2)
则由韦达定理: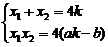 …………9分
…………9分
又过S、R点的切线方程分别为: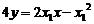 ,
,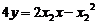 …11分
…11分
故有 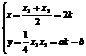 (k为参数)消去k,得:ax-2y-2b=0
(k为参数)消去k,得:ax-2y-2b=0
故B点恒在直线ax-2y-2b=0上. …………14分