
(1)掌握平面的基本性质,会用斜二测的画法画水平放置的平面图形的直观图.能够画出空间两条直线、直线和平面的各种位置关系的图形.能够根据图形想像它们的位置关系.
(2)掌握两条直线平行与垂直的判定定理和性质定理.掌握两条直线所成的角和距离的概念,对于异面直线的距离,只要求会计算已给出公垂线时的距离.
(3)掌握直线和平面平行的判定定理和性质定理.掌握直线和平面垂直判定定理和性质定理.掌握斜线在平面上的射影、直线和平面所成角、直线和平面的距离的概念.掌握三垂线定理及其逆定理.
(4)掌握两个平面平行的判定定理和性质定理.掌握二面角、二面角平面角、两个平行平面间的距离概念.掌握两个平面垂直的判定定理和性质定理.
(5)会用反证法证明简单的问题.
(6)了解多面体、凸多面体的概念,了解正多面体的概念.
(7)了解棱柱的概念,掌握棱柱的性质
(8)了解棱锥的概念,掌握正棱锥的性质
(9)了解球的概念,掌握球的性质,掌握球的表面积、体积公式.
1..证明直线与直线的平行的思考途径
(1)转化为判定共面二直线无交点;
(2)转化为二直线同与第三条直线平行;
(3)转化为线面平行;
(4)转化为线面垂直;
(5)转化为面面平行.
2.证明直线与平面的平行的思考途径
(1)转化为直线与平面无公共点;
(2)转化为线线平行;
(3)转化为面面平行.
3.证明平面与平面平行的思考途径
(1)转化为判定二平面无公共点;
(2)转化为线面平行;
(3)转化为线面垂直.
4.证明直线与直线的垂直的思考途径
(1)转化为相交垂直;
(2)转化为线面垂直;
(3)转化为线与另一线的射影垂直;
(4)转化为线与形成射影的斜线垂直.
5.证明直线与平面垂直的思考途径
(1)转化为该直线与平面内任一直线垂直;
(2)转化为该直线与平面内相交二直线垂直;
(3)转化为该直线与平面的一条垂线平行;
(4)转化为该直线垂直于另一个平行平面;
(5)转化为该直线与两个垂直平面交线垂直.
6.证明平面与平面的垂直的思考途径
(1)转化为判断二面角是直二面角;
(2)转化为线面垂直.
7.三余弦定理
设AC是α内的任一条直线,且BC⊥AC,垂足为C,又设AO与AB所成的角为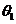 ,AB与AC所成的角为
,AB与AC所成的角为 ,AO与AC所成的角为
,AO与AC所成的角为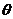 .则
.则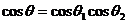 .
.
8. 长度为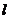 的线段在三条两两互相垂直的直线上的射影长分别为
的线段在三条两两互相垂直的直线上的射影长分别为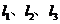 ,夹角分别为
,夹角分别为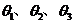 ,则有
,则有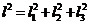
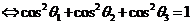
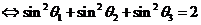 .
.
(长方体对角线长的公式是特例.
9. 面积射影定理 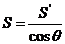 .(平面多边形及其射影的面积分别是
.(平面多边形及其射影的面积分别是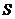 、
、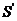 ,它们所在平面所成锐二面角的为
,它们所在平面所成锐二面角的为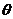 ).
).
10. 斜棱柱的直截面
已知斜棱柱的侧棱长是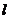 ,侧面积和体积分别是
,侧面积和体积分别是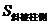 和
和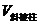 ,它的直截面的周长和面积分别是
,它的直截面的周长和面积分别是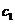 和
和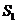 ,则
,则
①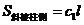 .②
.②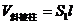 .
.
11.棱锥的平行截面的性质
如果棱锥被平行于底面的平面所截,那么所得的截面与底面相似,截面面积与底面面积的比等于顶点到截面距离与棱锥高的平方比(对应角相等,对应边对应成比例的多边形是相似多边形,相似多边形面积的比等于对应边的比的平方);相应小棱锥与小棱锥的侧面积的比等于顶点到截面距离与棱锥高的平方比.
12.球的半径是R,则
其体积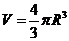 ,其表面积
,其表面积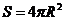 .
.
13.球的组合体
(1)球与长方体的组合体:
长方体的外接球的直径是长方体的体对角线长.
(2)球与正方体的组合体:
正方体的内切球的直径是正方体的棱长, 正方体的棱切球的直径是正方体的面对角线长, 正方体的外接球的直径是正方体的体对角线长.
(3) 球与正四面体的组合体:
棱长为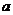 的正四面体的内切球的半径为
的正四面体的内切球的半径为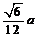 ,
,
外接球的半径为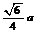 .
.
14.柱体、锥体的体积
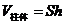 (
(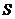 是柱体的底面积、
是柱体的底面积、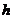 是柱体的高).
是柱体的高).
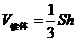 (
(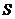 是锥体的底面积、
是锥体的底面积、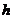 是锥体的高).
是锥体的高).
15.经纬度及球面距离
⑴根据经线和纬线的意义可知,某地的经度是一个二面角度数,某地的纬度是一个线面角度数,
⑵两点间的球面距离就是连结球面上两点的大圆的劣弧的长,因此,求两点间的球面距离的关键就在于求出过这两点的球半径的夹角。
16.二面角的求法
(1)定义法:直接在二面角的棱上取一点,分别在两个半平面内作棱的垂线,得出平面角,;
(2)三垂线法:已知二面角其中一个面内一点到一个面的垂线,用三垂线定理或逆定理作出二面角的平面角;
(3)垂面法:已知二面角内一点到两个面的垂线时,过两垂线作平面与两个半平面的交线所成的角即为平面角,由此可知,二面角的平面角所在的平面与棱垂直;
(4)射影法:利用面积射影公式S射=S原cos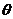 ,其中
,其中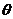 为平面角的大小,此方法不必在图形中画出平面角;
为平面角的大小,此方法不必在图形中画出平面角;
特别:对于一类没有给出棱的二面角,应先延伸两个半平面,使之相交出现棱,然后再选用上述方法(尤其要考虑射影法)。
17直线和平面所成的角:
(1)定义:平面的一条斜线和它在平面内的射影所成的锐角,叫这条直线和这个平面所成的角。
(2)范围: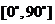 ;(3)求法:作出直线在平面上的射影;(4)斜线与平面所成的角的特征:斜线与平面中所有直线所成角中最小的角。
;(3)求法:作出直线在平面上的射影;(4)斜线与平面所成的角的特征:斜线与平面中所有直线所成角中最小的角。
18.空间距离的求法
(1)两异面直线间的距离,高考要求是给出公垂线,一般利用垂直作出公垂线,然后再进行计算;
(2)求点到直线的距离,一般用三垂线定理作出垂线再求解;
(3)求点到平面的距离,
一是用垂面法,借助面面垂直的性质来作,因此,确定已知面的垂面是关键;
二是不作出公垂线,转化为求三棱锥的高,利用等体积法列方程求解;
19。几个公式
(1).斜三棱柱的体积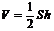 其中S表示一个侧面的面积,
其中S表示一个侧面的面积,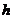 表示侧棱到相对的侧面的距离。该公式对于解决以知侧棱到相对侧面距离和该侧面面积求棱柱体积的问题非常有效。
表示侧棱到相对的侧面的距离。该公式对于解决以知侧棱到相对侧面距离和该侧面面积求棱柱体积的问题非常有效。
(2)直棱柱剪截体体积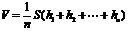 巧用
巧用
(3)长方体的对角线长的公式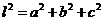
20.几个定理
1.两直线平行的判定:
(1)公理4:平行于同一直线的两直线互相平行;(2)线面平行的性质:如果一条直线和一个平面平行,那么经过这条直线的平面和这个平面相交的交线和这条直线平行;
(3)面面平行的性质:如果两个平行平面同时与第三个平面相交,那么它们的交线平行;
(4)线面垂直的性质:如果两条直线都垂直于同一个平面,那么这两条直线平行。
2、直线与平面的位置关系:
(1)直线在平面内;
(2)直线与平面相交。其中,如果一条直线和平面内任何一条直线都垂直,那么这条直线和这个平面垂直。注意:任一条直线并不等同于无数条直线;(3)直线与平面平行。其中直线与平面相交、直线与平面平行都叫作直线在平面外。
3、直线与平面平行的判定和性质:
①判定定理:如果平面内一条直线和这个平面平面平行,那么这条直线和这个平面平行;
②面面平行的性质:若两个平面平行,则其中一个平面内的任何直线与另一个平面平行。
性质:如果一条直线和一个平面平行,那么经过这条直线的平面和这个平面相交的交线和这条直线平行。在遇到线面平行时,常需作出过已知直线且与已知平面相交的辅助平面,以便运用线面平行的性质。
4、直线和平面垂直的判定和性质:
(1)判定:①如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线和这个平面垂直。②两条平行线中有一条直线和一个平面垂直,那么另一条直线也和这个平面垂直。
(2)性质:①如果一条直线和一个平面垂直,那么这条直线和这个平面内所有直线都垂直。②如果两条直线都垂直于同一个平面,那么这两条直线平行。
5、两个平面平行的判定和性质:
(1)判定:一个如果平面内有两条相交直线和另一个平面平行,则这两个平面平行。
(2)性质:如果两个平行平面同时与第三个平面相交,那么它们的交线平行。)