
直线的倾斜角和斜率、直线方程的点斜式、直线方程的斜截式
[知识点]
1. 直线的方程和方程的直线:
定义:
(1)以一个方程f(x,y)=0的解为坐标的点都在直线l上。
(2)直线l上的点的坐标都是方程f(x,y)=0的解。
满足(1)(2)的方程f(x,y)=0是直线l的方程,同时称直线l为方程f(x,y)=0的直线。
2. 直线的倾斜角:
定义:在平面直角坐标系中,对于一条与x轴相交的直线,如果把x轴绕交点逆时针旋转与直线重合时,所转过的最小正角为直线倾斜角。
规定:当直线与x轴平行或重合时,倾斜角为0°。
范围:0°≤α<180°
注意:(1)定义分两部分:一部分是与x轴相交,另一部分与x轴平行。
(2)与x轴相交的定义中,应理解三个地方:①x轴绕交点旋转;②逆时针方向;③最小正角。
(3)应特别注意倾斜角的范围[0,π)。
(4)任何一条直线有唯一倾斜角,表示直线的倾斜程度,但倾斜角为α的直线有无穷多条。
3. 直线的斜率:
定义:倾斜角不是90°的直线,其倾斜角的正切,叫做这条直线的斜率。
符号:常用k表示,即k=tanα。
注意:(1)所有直线都有倾斜角,但不是所有直线都有斜率。
调区间。
(3)当倾斜角为90°时斜率不存在,但直线存在。
4. 过两点的直线斜率公式:
公式推导:如图,已知直线l过两点P1(x1,y1),P2(x2,y2),倾斜角为α,求斜率k。
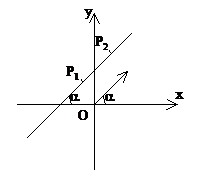
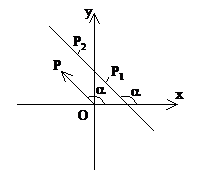
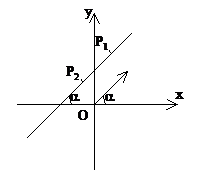
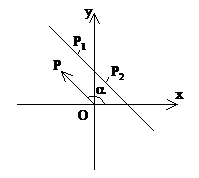

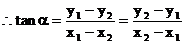
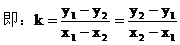
注意:(1)斜率公式与点的顺序无关。
(2)由公式可知表示直线倾斜程度,可以由直线上两点确点,无需求倾斜角。
(3)当x1=x2,y1≠y2时,α=90°没有斜率。
(4)利用公式求斜率时,应注意隐含条件x1≠x2。
5. 直线的方向向量:
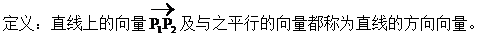
意义:表示直线的方向。
6. 直线方程的点斜式:
(1)方程的推导:略
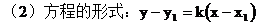
(3)方程的特殊情况:y=y1
(4)不能用点斜式表示的直线:x=x1
7. 直线方程的斜截式:
(1)方程的推导:(略)
(2)截距的概念:(是坐标不是距离)
(3)方程的形式:y=kx+b
(4)方程的特殊情况:y=0
(5)不能用斜截式表示的直线:x=0
[典型例题]
例1. 已知直线l的斜率k满足k>-2,求直线l的倾斜角的范围。
解:设直线l的倾斜角为α

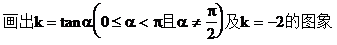
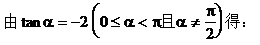
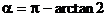
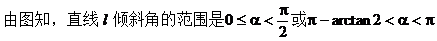
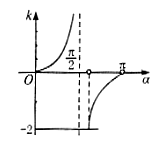
小结:已知直线l的斜率的范围,求直线l的倾斜角的范围时,常先画出函数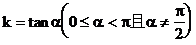 的图象,然后再由图象确定倾斜角的范围。
的图象,然后再由图象确定倾斜角的范围。
例2. 
求直线l的斜率。
解:设直线l的倾斜角为α,由题意知直线AB的倾斜角为2α
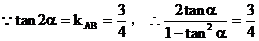
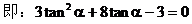
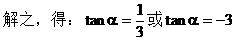
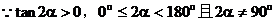
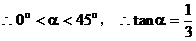
小结:由2α的正切值确定α的范围,及由α的范围求α的正切值是本例中易忽略的地方,在解同类型题的过程中应当注意。
例3. 求经过两点P1(2,1)和P2(m,2)(m∈R)的直线l的斜率,并且求出l的倾斜角α及其取值范围。
解:(1)当m=2时,x1=x2=2


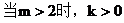

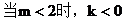
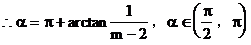
小结:利用斜率公式时,应注意公式的应用范围。当斜率k≥0时,直线的倾斜角为arctank;当k<0时,直线的倾斜角为π+arctank。
例4. 求证:A(1,-1)、B(-2,-7)、C(0,-3)三点共线。
证法一:∵A(1,-1)、B(-2,-7)、C(0,-3)
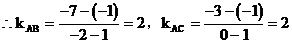
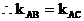
∴直线AB与直线AC倾角相同且过同一点A
∴直线AB与直线AC为同一条直线
故A、B、C三点共线
证法二:∵A(1,-1)、B(-2,-7)、C(0,-3)
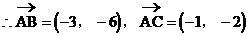
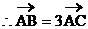
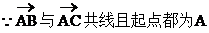
故A、B、C三点共线
小结:解法一是利用了直线上任意两个不同的点所确定的斜率都应相等这一思想方法。解法二利用了共线向量定理,此法较简单,此题还有其他一些解法。
例5. 已知两点A(-3,4)、B(3,2),过点P(2,-1)的直线l与线段AB有公共点。
(1)求直线l的斜率k的取值范围;
(2)求直线l的倾斜角α的取值范围。
解:如图所示,因为直线l与线段AB有公共点,所以l的倾斜角介于直线PB与直线PA的倾斜角之间,当l的倾斜角小于90°时,k≥kPB;当l的倾斜角大于90°时,k≤kPA。
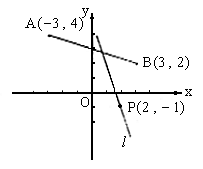
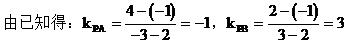
(1)∵l与线段AB有公共点
∴k的取值范围是k≤-1或k≥3。
(2)因为l的倾斜角介于直线PB的倾斜角和直线PA的倾斜角之间,又直线PB的倾斜角是arctan3,直线PA的倾斜角是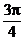
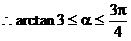
例6. 如图所示,直线l1、l2、l3的斜率分别为k1、k2、k3,则( )


(1995年全国高考题)
分析:根据直线的倾斜角与斜率的关系判断。
解:法一根据直线的斜率k与倾斜角α的关系k=tanα(0≤α<π),由图可见k2>k3>0>k1,故选D。
例7. 已知直线的倾斜角的取值范围,利用正切函数的性质,讨论直线斜率及其绝对值的变化情况。
(1)0°<α<90°;(2)90°<α<180°。
分析:本题要讨论的问题有两个:第一,直线斜率的变化情况;第二,直线斜率的绝对值的变化情况。
(2)首先要建立斜率k与倾斜角α之间的关系以及斜率k的绝对值|k|与倾斜角α之间的关系,然后讨论变化情况,必要时可先画出函数的图象,根据图象指出直线的斜率及其绝对值的变化情况。
(3)用函数的性质或图象知识去讨论。
解:当0°<α<90°时,tanα>0
(1)k=tanα,|k|=|tanα|=tanα(0°<α<90°)
∴y=k与y=|k|的图象相同(如图所示)
这时,直线的斜率与直线斜率的绝对值相等,且属于(0,+∞),直线的斜率及其绝对值随着直线倾斜角的增大而增大。

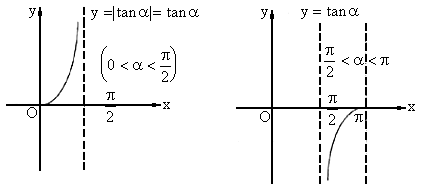
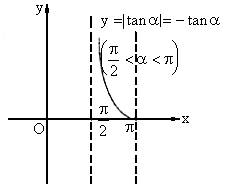
当90°<α<180°时,k=tanα<0

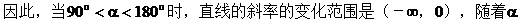

当0<α<90°时,直线斜率的变化范围是(0,+∞),随着倾斜角在开区间
当90°<α<180°时直线斜率绝对值的变化范围是(0,+∞),随着倾斜角在开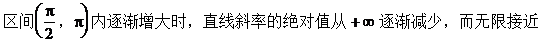
于0。
例8. 已知直线经过点P(3,2),倾斜角是直线x-4y+3=0的倾斜角的2倍,求直线l的方程。
解:设直线x-4y+3=0的倾斜角为α

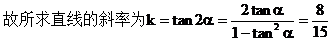
又直线经过点P(3,2)
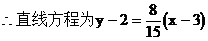

小结:先求出直线x-4y+3=0的倾斜角,然后求出直线l的倾斜角,最后代入点P求出解析式。
例9. 已知直线过点P(-2,3),且与两坐标轴围成的三角形面积为4,求直线的方程。
分析:关键是要求出斜率k。
解:显然,直线l与两坐标轴不垂直,设直线的方程为y-3=k(x+2)
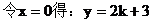
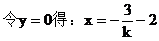

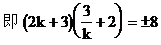


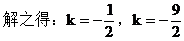
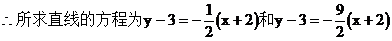
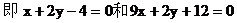
例10. 如果AC<0,且BC<0,那么直线Ax+By+C=0不通过( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
(1991年全国高考题.文)
答案:C
分析:先求出直线与两坐标轴的交点,再判断。
解:法一,由BC<0,知B≠0
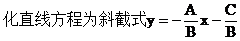
因为AC<0,BC<0,所以AB>0

所以直线不通过第三象限,故选C。
法二,取特殊值:A=B=1,C=-1知满足题设,此时方程为x+y-1=0,由其图象知,直线不通过第三象限,故选C。
例11. 
线方程
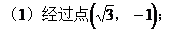
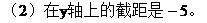
解: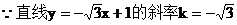
∴其倾斜角α=120°

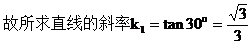
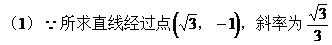
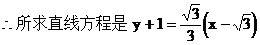
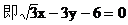

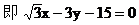
小结:

[模拟试题]
1. 直线 的倾斜角是( )
的倾斜角是( )
A. 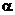 B.
B.
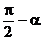
C. 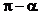 D.
D.
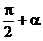
2. 若直线的斜率为k,并且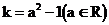 ,则直线l的倾斜角α的范围是__________。
,则直线l的倾斜角α的范围是__________。
3. 已知直线l过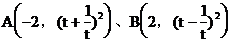 两点,则此直线的斜率和倾斜角分别为(
)
两点,则此直线的斜率和倾斜角分别为(
)
A. 1,135° B.
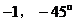
C. 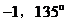 D.
1,45°
D.
1,45°
4. 过点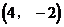 ,倾斜角为150°的直线的方程是( )
,倾斜角为150°的直线的方程是( )
A. 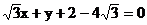
B. 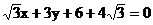
C. 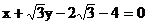
D. 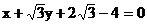
5. 已知直线的方程是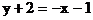 ,则( )
,则( )
A. 直线经过点(2,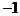 ),斜率为
),斜率为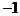
B. 直线经过点(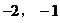 ),斜率为1
),斜率为1
C. 直线经过点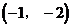 ,斜率为
,斜率为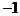
D. 直线经过点(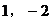 ),斜率为
),斜率为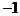
6. 直线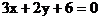 的斜率为k,在y轴上的截距为b,则有( )
的斜率为k,在y轴上的截距为b,则有( )
A. 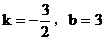
B. 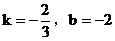
C. 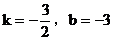
D. 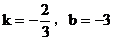
7. 若直线l的倾斜角为α,并且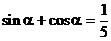 ,求直线l的斜率k。
,求直线l的斜率k。
8. 已知某直线的倾斜角α满足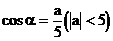 ,求该直线的斜率。
,求该直线的斜率。
9. 已知直线l过点A(2,-1),倾斜角α的范围是 。在直角坐标系中给定两点
。在直角坐标系中给定两点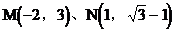 ,问l与线段MN是否有交点?若有交点,请说明理由。
,问l与线段MN是否有交点?若有交点,请说明理由。
10. 分别在下列条件下求直线的倾斜角和斜率。
(1)直线l的倾斜角的正弦值为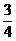 ;
;
(2)直线l的方向向量为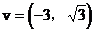 。
。

直线的倾斜角和斜率、直线方程的点斜式、直线方程的斜截式参考答案
[试题答案]
1. 答案:D
解析:把直线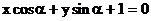 写成
写成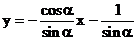
 ,而
,而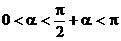
∴直线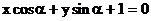 的倾斜角是
的倾斜角是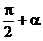
2. 答案: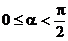 或
或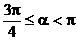
解析: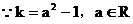
 ,即
,即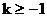
由函数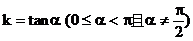 的图象及
的图象及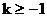 ,知l的倾斜角α的范围是
,知l的倾斜角α的范围是
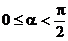 或
或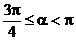
3. 答案:C
解析: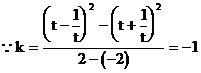
∴直线的倾斜角为135°
4. 答案:D
所求直线的斜率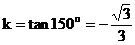
由点斜式得:
即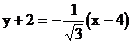
故所求直线方程为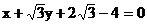
5. 答案:C
解析:直线方程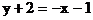 可化为
可化为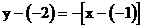
故直线过点( ),斜率为
),斜率为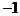
6. 答案:C
解析:直线方程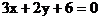 化为斜截式得:
化为斜截式得:
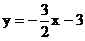 故
故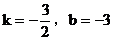
7. 解: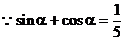
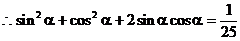
即 
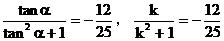
解之,得: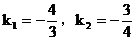
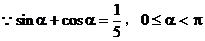
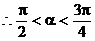
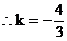 为所求
为所求
8. 解:当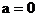 时,
时,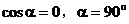 ,该直线的斜率不存在。
,该直线的斜率不存在。
当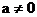 时,
时,
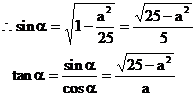
综上所述,当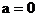 时,所求直线的斜率不存在;
时,所求直线的斜率不存在;
当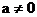 时,所求直线的斜率为
时,所求直线的斜率为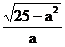 。
。
9. 解:l与线段MN有交点
因为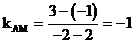 ,所以直线AM的倾斜角为
,所以直线AM的倾斜角为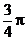 。
。
因为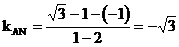 ,所以直线AN的倾斜角为
,所以直线AN的倾斜角为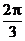 。
。
因为l的倾斜角α的范围是 ,所以l与线段MN有交点。
,所以l与线段MN有交点。
10. 分析:(1)由已知条件求出直线的倾斜角,再求直线的斜率。注意到在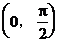 与
与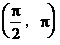 内角的正弦值都取正值,因此用反正弦表示角时,应区分角是锐角还是钝角。
内角的正弦值都取正值,因此用反正弦表示角时,应区分角是锐角还是钝角。
(2)利用方向向量与x轴所夹的最小正角与l的倾斜角相等求解。
解:(1)设直线l的倾斜角为α,则
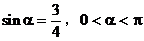
当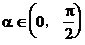 时,
时,

当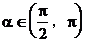 时,
时,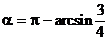

(2)法一:∵v是l的方向向量
∴v∥l
∴v与x轴所夹的最小正角与l的倾斜角α相等,则
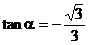
∴l的斜率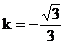 ,倾斜角为
,倾斜角为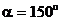
法二:设l的斜率为k,则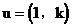 是l的一个方向向量
是l的一个方向向量
由已知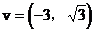 是l的一个方向向量
是l的一个方向向量
∴u∥v,则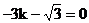
即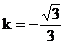
∴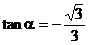 ,倾斜角为
,倾斜角为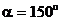
[励志故事]
沉静--思考--判断--成功
从前有位地主巡视谷仓时,不慎将一只名表遗失,因遍寻不获,便定下赏金,要农场上的小孩帮忙寻找,谁能找到手表,奖金500美元。众小孩在重赏之下,无不卖力搜寻,奈何谷仓内到处都是成堆的谷粒和稻草,大家忙到太阳下山仍无所获,结果一个接着一个都放弃了。
只有一个贫穷小孩,为了那笔巨额奖金,仍不死心地寻找。当天色渐黑,众人离去,杂沓人声静下来之后,他突然听到一个奇怪的声音。那声音“滴答、滴答”不停地响着,小孩立刻停下所有的动作,谷仓内更安静了,滴答声也响得更为清晰。小孩循着声音,终于在诺大漆黑的谷仓中找到了那只名贵手表。
“静坐无所为,春来草自青。”
惟有让流水平静下来,太阳和月亮才能在它的表面上显现倒影。
当人沉静下来,才能看出所有干扰清晰思考,蒙蔽真实感情,影响智慧判断,以及阻碍自己找到答案的问题所在。
在自己的内心保留一处梦想可以停驻的宁静地方。