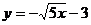1、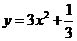 已知P为抛物线
已知P为抛物线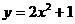 上的动点,定点A(0,1),点M分
上的动点,定点A(0,1),点M分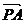 所成的比为2,则点M的轨迹方程为( )
所成的比为2,则点M的轨迹方程为( )
A、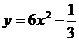 B、
B、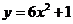 C、
D、
C、
D、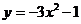
2、已知点F1(-4,0),F2(4,0),又P(x,y)是曲线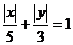 上的点,则( )
上的点,则( )
A、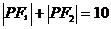 B、
B、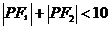
C、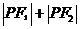 ≤10
D、
≤10
D、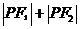 ≥10
≥10
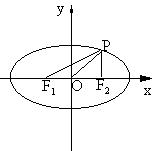
3、已知点P是椭圆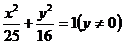 上的动点,F1,F2为椭圆的两个焦点,O为坐标原点,若M是∠F1PF2的角平分线上一点,
上的动点,F1,F2为椭圆的两个焦点,O为坐标原点,若M是∠F1PF2的角平分线上一点,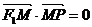 ,则
,则 取值范围是(
)
取值范围是(
)
A、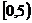 B、
B、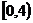 C、
C、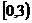 D、
D、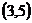
4、已知F1,F2分别为双曲线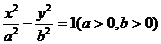 的左右焦点,P为双曲线左支上任意一点,若
的左右焦点,P为双曲线左支上任意一点,若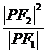 最小值是8
最小值是8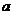 ,则双曲线离心率e的取值范围是( )
,则双曲线离心率e的取值范围是( )
A、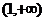 B、
B、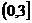 C、
C、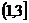 D、
D、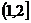
1、由动点P向圆x2+y2=1引两条切线PA,PB,切点分别为A,B,∠APB= 则动点P的轨迹方程是
则动点P的轨迹方程是
2、已知椭圆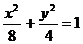 ,P为椭圆上任意一点,F1,F2分别为椭圆的左、右焦点,则
,P为椭圆上任意一点,F1,F2分别为椭圆的左、右焦点,则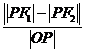 的范围是
的范围是
1、已知O为坐标原点,P( )(
)(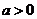 )为
)为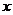 轴上一动点,过P作直线交抛物线
轴上一动点,过P作直线交抛物线 于A、B两点,设S△AOB=
于A、B两点,设S△AOB=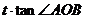 ,试问:
,试问: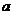 为何值时,t取得最小值,并求出最小值。
为何值时,t取得最小值,并求出最小值。
2、若F1,F2为双曲线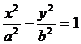 的左、右焦点,0为坐标原点,P在双曲线左支上,M在右准线上,且满足
的左、右焦点,0为坐标原点,P在双曲线左支上,M在右准线上,且满足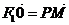 ,
,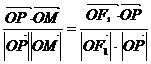
① 求此双曲线离心率
②若双曲线过点N(2,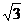 ),虚轴端点为B1,B2(B1在y 轴正半轴上),点A,B在双曲线上,且
),虚轴端点为B1,B2(B1在y 轴正半轴上),点A,B在双曲线上,且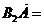 λ
λ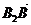
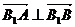 ,求直线AB方程。
,求直线AB方程。
答案详解:
1、设M(x,y) P (x0,y0)
∵M分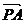 所成的比为2
所成的比为2
∴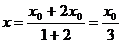
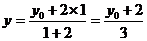
∴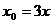
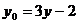 又
又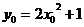
∴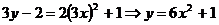 应选B
应选B
2、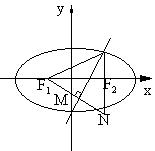 考察曲线
考察曲线 及椭圆
及椭圆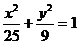 图形
图形
由随圆第一定义可得:
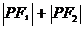 ≤2
≤2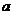 =10 应选C
=10 应选C
3、由对称性不妨设P位于第一家限,延长F1M交PF2于N,可得M为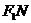 中点
中点
∴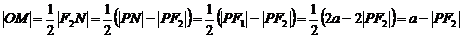
∵P在第一部分 ∴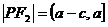
∴0≤ 即0≤
即0≤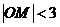 应选C
应选C
4、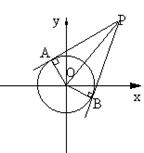
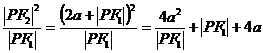 ≥8
≥8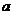 可得
可得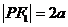
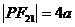 由三角形边角关系可得:
由三角形边角关系可得:
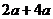 ≥
≥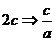 ≤3 应选C
≤3 应选C
1、 设P(x,y) 在Rt△AOP中,∠APO=30°
 sin30° ∴1=
sin30° ∴1=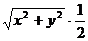 ∴
∴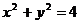
2、设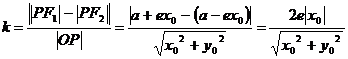
 当
当 时
时 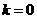
当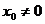 时
时
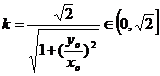
∴0≤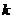 ≤
≤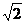
1、解:交AB与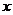 轴不重叠时,设AB的方程为
轴不重叠时,设AB的方程为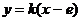
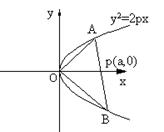 合
合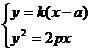 消y可得:
消y可得: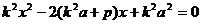
设A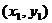 B
B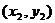 则
则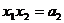 ,
,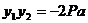 交AB与x轴重叠时,上述结论仍然成立
交AB与x轴重叠时,上述结论仍然成立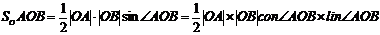
∴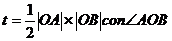 又
又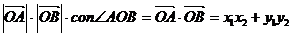
∴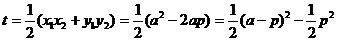 ≥
≥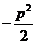
当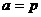 时 取“=”, 综上 当
时 取“=”, 综上 当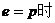
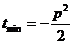
2、(1)由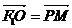 知四边形PF1OM为平行四边形
知四边形PF1OM为平行四边形
又由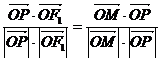 知OP平分
知OP平分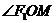
∴四边形PF1OM为棱形
设半焦距为C,由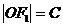 知
知
∴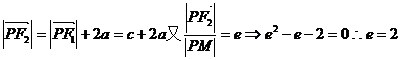
(2)∵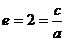 ∴
∴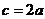 ∴双曲线方程为
∴双曲线方程为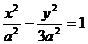
∵点(2,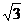 )在双曲线上 所以有
)在双曲线上 所以有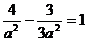 ∴
∴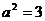
∴双曲线方程为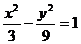 ∴
∴
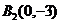 ∵
∵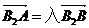
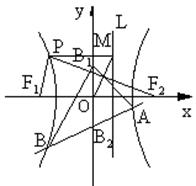
∴A,B2,B其线设自线AB的方程为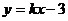 ,A
,A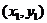 B
B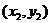
合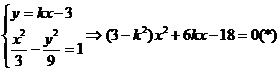 ∵AB与双曲线有两个交点
∵AB与双曲线有两个交点
∴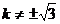 ∵
∵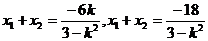
∴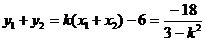
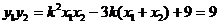
又∵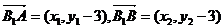
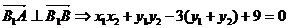 ∴
∴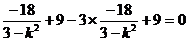
得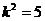 ∴
∴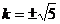
 经检验,此时适合公式中O>0
经检验,此时适合公式中O>0
故所求自成方程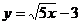 成
成