
1.化简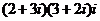 (其中i是虚数单位)的结果是( )
(其中i是虚数单位)的结果是( )
A.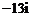 B.
B.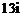 C.
C.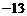 D.13
D.13
2.双曲线 的两条准线间的距离等于( )
的两条准线间的距离等于( )
A.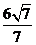 B.
B. C.
C.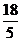 D.
D.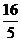
3.已知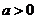 ,
,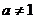 ,函数
,函数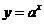 ,
,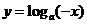 的图象大致是下面的( )
的图象大致是下面的( )
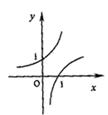
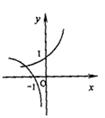
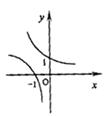
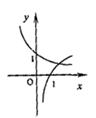
A B C D
4.若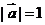 ,
,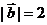 ,
, ,且
,且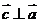 ,则向量
,则向量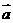 与
与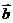 的夹角是( )
的夹角是( )
A.30° B.60° C.120° D.150°
5.在2006年北京国际汽车展上,某汽车生产厂家准备推出10款不同的轿车参加车展,若主办方只能为该厂提供6个展位,每个展位摆放一辆车,且甲、乙两款车不能摆放在2号展位上,则该厂家参展轿车的不同摆放方案有( )
A. 种 B.
种 B.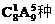 C.
C.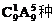 D.
D.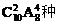
6.若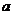 、
、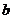 为空间两条不同的直线,
为空间两条不同的直线,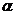 、
、 为空间两个不同的平面,则
为空间两个不同的平面,则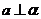 的一个充分条件是( )
的一个充分条件是( )
A.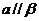 且
且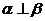 B.
B.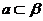 且
且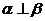
C.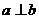 且
且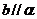 D.
D.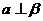 且
且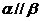
7.在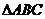 中,已知
中,已知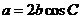 ,那么这个三角形一定是( )
,那么这个三角形一定是( )
A.等边三角形 B.直角三角形
C.等腰三角形 D.等腰直角三角形
8.已知椭圆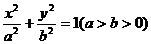 与双曲线
与双曲线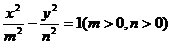 有相同的焦点
有相同的焦点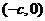 和
和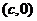 ,若
,若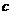 是
是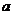 与
与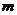 的等比中项,
的等比中项,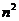 是
是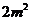 与
与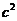 的等差中项,则该椭圆的离心率是( )
的等差中项,则该椭圆的离心率是( )
A.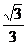 B.
B.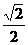 C.
C.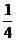 D.
D.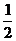
9.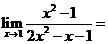 ___________.
___________.
10.在△ABC中,若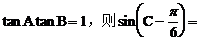 ____________.
____________.
11.在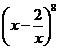 展开式中,常数项是__________________,展开式中各项系数和为__________.(用数字作答)
展开式中,常数项是__________________,展开式中各项系数和为__________.(用数字作答)
12.已知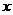 ,
,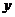 满足
满足 ,则函数
,则函数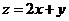 的最大值是______________.
的最大值是______________.
13.在等差数列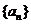 中,
中, 为数列
为数列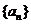 的前
的前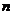 项和,且
项和,且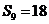 ,
,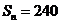 ,若
,若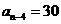
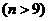 ,则
,则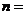 __________________.
__________________.
14.已知点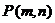 位于第一象限,且在直线
位于第一象限,且在直线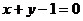 上,则使
上,则使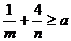 恒成立的实数a的取值范围是__________________.
恒成立的实数a的取值范围是__________________.
高三数学综合练习
班级________ 姓名__________ 成绩___________
|
题 号 |
一 |
二 |
三 |
|||||
|
15 |
16 |
17 |
18 |
19 |
20 |
|||
|
得 分 |
|
|
|
|
|
|
|
|
15.本小题满分12分
已知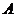 、
、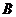 、
、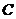 三点的坐标分别为
三点的坐标分别为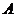
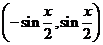 ,
,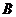
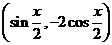 ,
,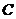
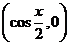 .
.
⑴ 求向量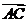 和向量
和向量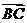 的坐标;
的坐标;
⑵ 设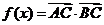 ,求
,求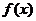 的最小正周期;
的最小正周期;
⑶ 求当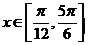 时,
时,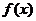 的最大值及最小值.
的最大值及最小值.
16.本小题满分14分
在某次测试中,甲、乙、丙三人能达标的概率分别为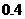 ,
,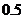 ,
,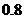 ,在测试过程中,甲、乙、丙能否达标彼此间不受影响.
,在测试过程中,甲、乙、丙能否达标彼此间不受影响.
⑴ 求甲、乙、丙三人均达标的概率;
⑵ 求甲、乙、丙三人中至少一人达标的概率;
⑶ 设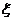 表示测试结束后达标人数与没达标人数之差的绝对值,求
表示测试结束后达标人数与没达标人数之差的绝对值,求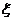 的概率分布及数学期望
的概率分布及数学期望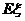 .
.
17.本小题满分13分
已知函数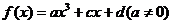 是
是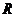 上的奇函数,当
上的奇函数,当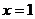 时,
时,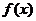 取得极值
取得极值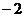 .
.
⑴ 求函数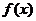 的解析式;
的解析式;
⑵ 求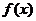 的单调区间;
的单调区间;
⑶ 当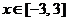 时,
时,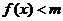 恒成立,求实数
恒成立,求实数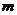 的取值范围.
的取值范围.
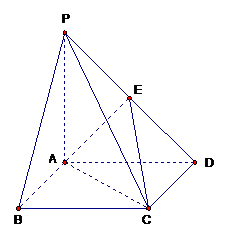
18.本小题满分14分
如图,在四棱锥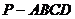 中,四边形
中,四边形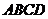 为正方形,
为正方形,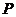 点在平面
点在平面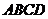 内的射影为
内的射影为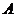 ,且
,且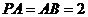 ,
,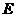 为
为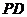 中点.
中点.
⑴ 证明: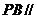 平面
平面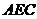 ;
;
⑵ 证明:平面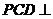 平面
平面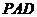 ;
;
⑶ 求二面角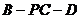 的大小.
的大小.
19.本小题满分13分
已知数列 满足
满足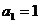 ,且
,且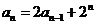
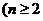 ,且
,且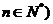 .
.
⑴ 求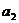 ,
,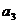 ;
;
⑵ 证明数列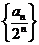 是等差数列;
是等差数列;
⑶ 求数列 的前
的前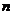 项之和
项之和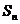 .
.
20.本小题满分14分
设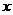 ,
,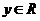 ,
,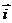 ,
,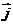 为直角坐标平面内
为直角坐标平面内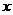 ,
,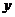 轴正方向上的单位向量,若
轴正方向上的单位向量,若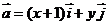 ,
, ,
,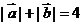 .
.
⑴ 求点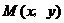 的轨迹
的轨迹 的方程;
的方程;
⑵ 过点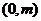 作直线
作直线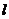 与曲线
与曲线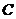 交于
交于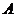 、
、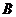 两点,若
两点,若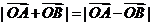 ,求
,求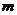 的取值范围.
的取值范围.