
1.在△ABC中,角A、B、C的对边分别为a、b、c,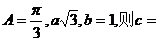 ( )
( )
A.1 B.2 C.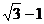 D.
D.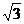
2.已知命题P: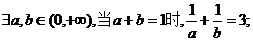 命题
命题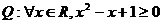
恒成立,则下列命题是假命题的是( )
A.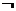 P∨
P∨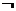 Q B.
Q B.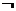 P∧
P∧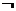 Q C.
Q C.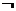 P∨Q D.
P∨Q D.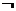 P∧Q
P∧Q
3.已知圆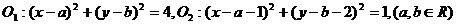 那么两圆的位置关系是 ( )
那么两圆的位置关系是 ( )
A.内容 B.内切 C.相交 D.外切
4.右图为一个几何体的三视国科,尺寸如图所示,则该几何体的表面积(不考虑接触点)
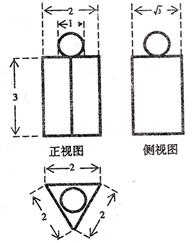 为( )
为( )
A.6+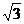 +
+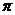
B.18+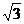 +4
+4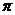
|
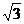 +
+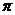
D.32+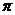
5.函数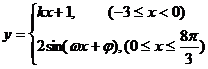 的图象如下图,则 ( )
的图象如下图,则 ( )
 A.
A.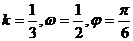
B.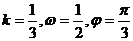
C.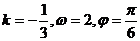
D.
6.如果函数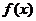 在区间D上是“凸函数”,则对于区间D内任意的
在区间D上是“凸函数”,则对于区间D内任意的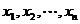 ,有
,有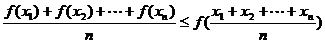 成立. 已知函数
成立. 已知函数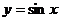 在区间[0,π]上是“凸函数”,则在△ABC中,
在区间[0,π]上是“凸函数”,则在△ABC中, 的最大值是( )
的最大值是( )
A.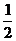 B.
B.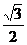 C.
C.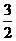 D.
D.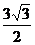
7.某种游戏中,黑、黄两个“电子狗”从棱长为1的正方体ABCD-A1B1C1D1的顶点A出发沿棱向前爬行,每爬完一条棱称为“爬完一段”,黑“电子狗”爬行的路线是AA1→A1D1→…,黄“电子狗”爬行的路线是AB→BB1→…,它们都遵循如下规则:所爬行的第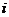 +2段与第
+2段与第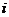 段所在直线必须成异面直线(其中
段所在直线必须成异面直线(其中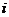 是正整数).设黑“电子狗”爬完2006段、黄“电子狗”爬完2005段后各自停止在正方体的某个顶点处,这时黑、黄“电子狗”间的距离是
(
)
是正整数).设黑“电子狗”爬完2006段、黄“电子狗”爬完2005段后各自停止在正方体的某个顶点处,这时黑、黄“电子狗”间的距离是
(
)
A.0
B.1 C.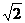 D.
D.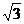
8.如果一对兔子每月能生产一对(一雌一雄)小兔子,而每一对小兔子在它出生的第三个月里,又能生产一对小兔子. 假定在不发生死亡的情况下,由一对初生的小兔子从第一个月开始,如果用a1表示初生小兔子的对数,an表示第n个月的兔子总对数,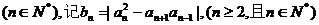 那么以下结论正确的是( )
那么以下结论正确的是( )
A.bn是n无关的常量
B.bn是n有关的变量,且既有最大值,又有最小值
C.bn是n有关的变量,且有最小值,但无最大值
D.bn是n有关的变量,且既有最大值,但无最小值
9.一个高中研究性学习小组对本地区2002年至2004年快餐公司发展情况进行了调查,制成了该地区快餐公司个数情况的条形图和快餐公司盒饭年销售量的平均数情况条形图(如图),根据图中提供的信息可以得出这三年中该地区每年平均销售盒饭__________万盒。

10.对于函数y=f(x),xÎD,若存在常数c,使对任意x1ÎD,存在唯一的x2ÎD,满足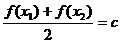 ,则称函数f(x)在D上的均值为c,现已知函数:① y=2x,② y=x5,③ y=2sinx,④ y=lgx,则满足在其定义域上均值为2的函数的序号是__________(填上所有符合要求的函数的序号)。
,则称函数f(x)在D上的均值为c,现已知函数:① y=2x,② y=x5,③ y=2sinx,④ y=lgx,则满足在其定义域上均值为2的函数的序号是__________(填上所有符合要求的函数的序号)。
11.等比数列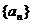 的公比为
的公比为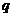 ,其前
,其前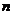 项的积为
项的积为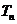 ,并且满足条件
,并且满足条件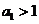 ,
,
 ,
,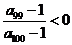 。给出下列结论:①
。给出下列结论:①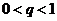 ;②
;②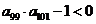 ③
③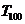 的值是
的值是 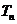 中最大的;④使
中最大的;④使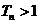 成立的最大自然数
成立的最大自然数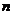 等于198。
等于198。
其中正确的结论是 .
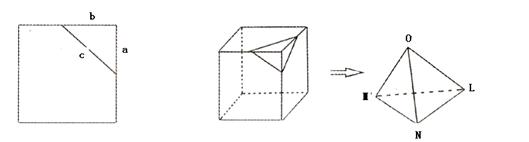
12.在平面上,我们如果用一条直线去截正方形的一个角,那么截下的一个直角三角形,按图所标边长,由勾股定理有: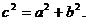
设想正方形换成正方体,把截线换成如图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥O-LMN,如果用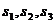 表示三个侧面面积,
表示三个侧面面积,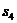 表示截面面积,那么你类比得到的结论是
.
表示截面面积,那么你类比得到的结论是
.
13.在极坐标系中,定点 ,点B在直线
,点B在直线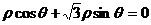 上运动,当线段AB最短时,点B的极坐标为__________.
上运动,当线段AB最短时,点B的极坐标为__________.
14.考察下列一组不等式: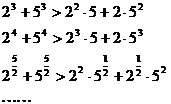 将上述不等式在左右两端视为两项和的情况下加以推广,使以上的不等式成为推广不等式的特例,则推广的不等式为 .
将上述不等式在左右两端视为两项和的情况下加以推广,使以上的不等式成为推广不等式的特例,则推广的不等式为 .
(本题满分12分)
15.设向量 .
.
|
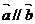 ,求
,求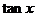 的值;
的值;
(2)求函数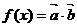 的最大值及相应x的值.
的最大值及相应x的值.
16.(本题满分12分)
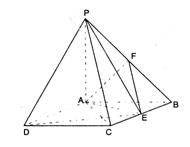 如图:四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=
如图:四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=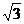 ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.
(Ⅰ)点E为BC的中点时,试判断EF与平面
PAC的位置关系,并说明理由;
(Ⅱ)证明:无论点E在BC边的何处,都有PE⊥AF;
(Ⅲ)当BE等于何值时,PA与平面PDE所成角的大小为45°
17.(本小题满分14分)班主任为了对本班学生的考试成绩进行分析,决定从全班25名女同学,15名男同学中随机抽取一个容量为8的样本进行分析.
(Ⅰ)如果按性别比例分层抽样,可以得到多少个不同的样本?(只要求写出算式即可,不必计算出结果).(Ⅱ)随机抽出8位,他们的数学分数从小到大排序是:60、65、70、75、80、85、90、95,物理分数从小到大排序是:72、77、80、84、88、90、93、95.
(1)若规定85分以上(包括85分)为优秀,求这8位同学中恰有3位同学的数学和物理分数均为优秀的概率;(2)若这8位同学的数学、物理分数对应如下表:
|
学生编号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
数学分数x |
60 |
65 |
70 |
75 |
80 |
85 |
90 |
95 |
|
物理分数y |
72 |
77 |
80 |
84 |
88 |
90 |
93 |
95 |
根据上表数据用变量y与x的相关系数或散点图说明物理成绩y与数学成绩x之间是否具有线性相关性?如果具有线性相关性,求y与x的线性回归方程(系数精确到0.01);如果不具有线性相关性,请说明理由.
参考公式:相关系数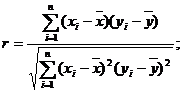 回归直线的方程是:
回归直线的方程是: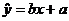 ,
,
其中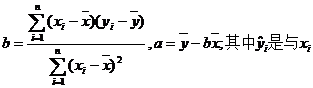 对应的回归估计值.
对应的回归估计值.
参考数据: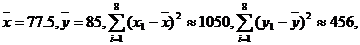
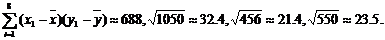
|
18.(本小题满分14分)
 已知点C为圆
已知点C为圆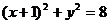 的圆心,点A(1,0),P是圆上的动点,点Q在圆的半径CP上,且
的圆心,点A(1,0),P是圆上的动点,点Q在圆的半径CP上,且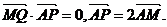
(Ⅰ)当点P在圆上运动时,求点Q的轨迹方程;
(Ⅱ)若直线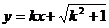 与(Ⅰ)中所求点Q
与(Ⅰ)中所求点Q
的轨迹交于不同两点F,H,O是坐标原点,
且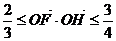 ,求△FOH的面积.
,求△FOH的面积.
19.(本小题满分14分)
各项均为正数的数列{an}的前n项和Sn,函数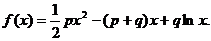
(其中p、q均为常数,且p>q>0),当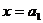 时,函数f(x)取得极小值,点
时,函数f(x)取得极小值,点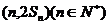 均在函数
均在函数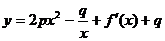 的图象上,(其中f′(x)是函数f(x)的导函数)
的图象上,(其中f′(x)是函数f(x)的导函数)
(1)求a1的值;
(2)求数列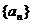 的通项公式;
的通项公式;
(3)记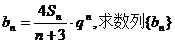 的前n项和Tn.
的前n项和Tn.
20.(本小题满分14分)
设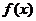 是定义在
是定义在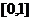 上的函数,若存在
上的函数,若存在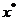
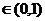 ,使得
,使得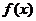 在
在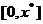 上单调递增,在
上单调递增,在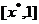 上单调递减,则称
上单调递减,则称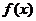 为
为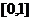 上的单峰函数,
上的单峰函数,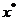 为峰点,包含峰点的区间为含峰区间. 对任意的
为峰点,包含峰点的区间为含峰区间. 对任意的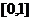 上的单峰函数
上的单峰函数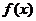 ,下面研究缩短其含峰区间长度的方法.
,下面研究缩短其含峰区间长度的方法.
(1)证明:对任意的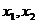
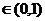 ,
,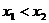 ,若
,若 ,则
,则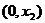 为含峰区间;若
为含峰区间;若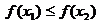 ,则
,则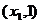 为含峰区间;
为含峰区间;
(2)对给定的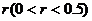 ,证明:存在
,证明:存在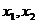
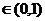 ,满足
,满足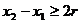 ,使得由(1)所确定的含峰区间的长度不大于
,使得由(1)所确定的含峰区间的长度不大于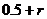 ;
;
高考数学综合模拟试卷(一)参考答案
参考答案
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
答案 |
B |
B |
C |
C |
A |
D |
D |
A |
9.85 10.②④ 11.
①②④ 12. 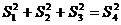
13. 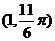 14.
14. 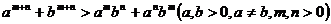
15.解:(I)∵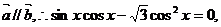 ……………………3分
……………………3分
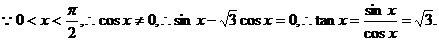 …6分
…6分
(Ⅱ)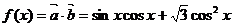 …………………………8分
…………………………8分
=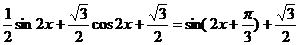 .………………10分
.………………10分
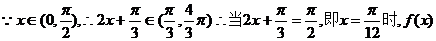
|
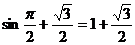 ………………………………12分
………………………………12分
16.解法1:(I)当点E为BC的中点时,
EF与平面PAC平行.∵在△PBC中,
E、F分别为BC、PB的中点,
∴EF//PC 又EF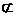 平面PAC,
平面PAC,
而PC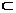 平面PAC ∴EF//平面PAC.…4分
平面PAC ∴EF//平面PAC.…4分
(II)证明:∵PA⊥平面ABCD,BE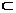 平面ABCD,
平面ABCD,
∴EB⊥PA.又EB⊥AB,AB∩AP=A,AB,AP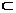 平面PAB,
平面PAB,
∴EB⊥平面PAB,
又AF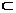 平面PAB,∴AF⊥BE.
平面PAB,∴AF⊥BE.
又PA=AB=1,点F是PB的中点,∴AF⊥PB,……………………4分
又∵PB∩BE=B,PB,BE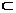 平面PBE,∴AF⊥平面PBE.
平面PBE,∴AF⊥平面PBE.
∵PE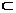 平面PBE,∴AF⊥PE.……………………8分
平面PBE,∴AF⊥PE.……………………8分
(Ⅲ)过A作AG⊥DE于G,连PG,又∵DE⊥PA,则DE⊥平面PAG,
于是,平面PAG⊥平面PDE,它们的交线是PG,过A作AM⊥PG,垂足为M,则AM⊥平面PDE,即PA在平面PDE的射影是PM,所以PA与平面PDE所成的角是∠APG=45°.
∴在RtPAG中,PA=AG=1,∴DG=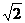 ,………………10分
,………………10分
设BE=x,∵△AGE≌△ABE,则GE=x,CE=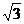 -x,
-x,
|
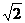 +x)2=(
+x)2=(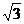 -x)2+12,得BE=x=
-x)2+12,得BE=x=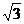 -
-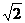 .……12分
.……12分
解法二: (II)建立图示空间直角坐标系,
则P(0,0,1),B(0,1,0),
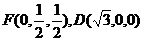 设
设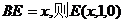
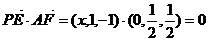 ∴AF⊥PE …8分
∴AF⊥PE …8分
(Ⅲ)设平面PDE的法向量为

而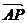 =(0,0,1)依题意PA与平面PDE所成角为45°,
=(0,0,1)依题意PA与平面PDE所成角为45°,
所以sin45°=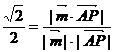 ,
,
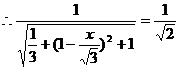 ,
,
得BE=x=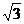 -
-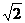 ,或BE=x=
,或BE=x=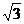 +
+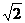 (舍).……………………12分
(舍).……………………12分
17.解:(I)应选女生25×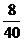 =5(个),男生15×
=5(个),男生15×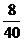 =3(个),可以得到不同的样本个数是
=3(个),可以得到不同的样本个数是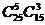 .……4分(II)(1)这8位同学中恰有3位同学的数学和物理分数均为优秀,则需要先从物理的4个优秀分数中选出3个与数学优秀分数对应,种数是
.……4分(II)(1)这8位同学中恰有3位同学的数学和物理分数均为优秀,则需要先从物理的4个优秀分数中选出3个与数学优秀分数对应,种数是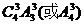 ,然后剩下的5个数学分数和物理分数任意对应,种数是
,然后剩下的5个数学分数和物理分数任意对应,种数是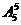 。根据乘法原理,满足条件的种数是
。根据乘法原理,满足条件的种数是 …………………………………………6分
…………………………………………6分
这8位同学的物理分数和数学分数分别对应的种数共有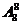 .…………7分
.…………7分
故所求的概率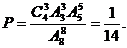 ………………………………10分
………………………………10分
|
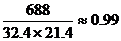 .可以看出,物理与数学成绩是高度正相关.若以数学成绩x为横坐标,
.可以看出,物理与数学成绩是高度正相关.若以数学成绩x为横坐标,
物理成绩y为纵坐标做散点图如下
从散点图可以看出这些点大至分布
在一条直线附近,并且在逐步上升,
故物理与数学成绩是高度正相关.
………………………………12分
设y与x线性回归方程y=bx+a、
根据所给的数据,可以计算出
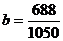 =0.65,a=85-0.65×77.5=34.63,
=0.65,a=85-0.65×77.5=34.63,
所以y与x的回归方程是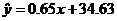 .……………………14分
.……………………14分
18. 解:(1)由题意MQ是线段AP的垂直平分线,于是
|CP|=|QC|+|QP|=|QC|+|QA|=2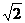 >|CA|=2,于是点 Q的轨迹是以点C,A为焦点,半焦距c=1,长半轴a=
>|CA|=2,于是点 Q的轨迹是以点C,A为焦点,半焦距c=1,长半轴a=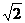 的椭圆,短半轴
的椭圆,短半轴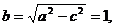
点Q的轨迹E方程是: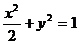 .…………………………4分
.…………………………4分
(2)设F(x1,y1)H(x2,y2),则由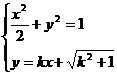 ,
,
消去y得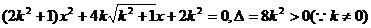
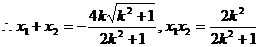 …………………………6分
…………………………6分
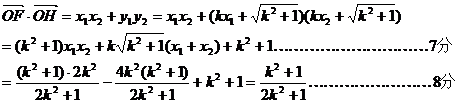
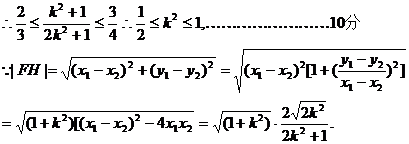
又点O到直线FH的距离d=1,
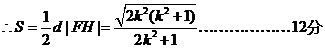
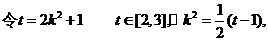

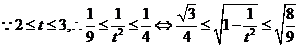

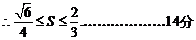
19. 解:(I)解: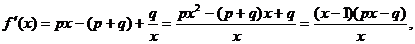
令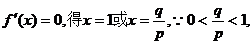
当x=变化时,f′(x),f(x)的变化情况如下表:
|
|
(0,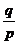 ) ) |
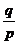 |
(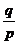 ,1) ,1) |
1 |
(1,+∞) |
|
f′(x) |
+ |
0 |
- |
0 |
+ |
|
f(x) |
 |
极大值 |
 |
极小值 |
 |
所以f(x)在x=1处取得最小值,即a1=1.………………………………5分
(II)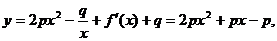
 ,
,
由于a1=1,所以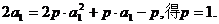 ………6分
………6分
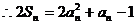 ……………………①.………………………………8分
……………………①.………………………………8分
又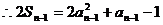 …………………………②。
…………………………②。
①-②得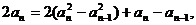
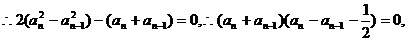
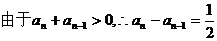 ,所以{an}是以a1=1,公差为
,所以{an}是以a1=1,公差为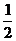 的等差数列,
的等差数列,
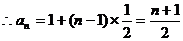 .………………………………10分
.………………………………10分
(Ⅲ)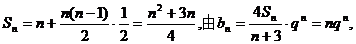

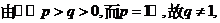
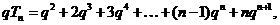
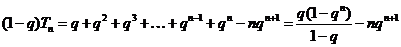
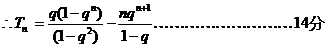
20. (1)证明:设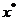 为
为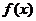 的峰点,则由单峰函数定义可知,
的峰点,则由单峰函数定义可知, 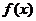 在
在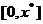 上单调递增, 在
上单调递增, 在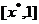 上单调递减,
上单调递减,
当 时,假设
时,假设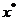
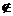
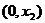 ,则
,则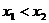 <
<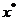 ,从而
,从而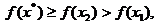 这与
这与 矛盾,所以
矛盾,所以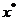
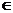
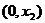 ,即
,即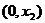 为含峰区间.
为含峰区间.
当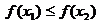 时,假设
时,假设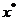
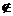
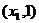 ,则
,则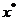
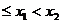 ,从而
,从而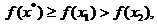 这与
这与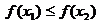 矛盾,所以
矛盾,所以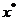
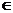
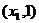 ,即
,即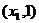 为含峰区间………………………….(7分)
为含峰区间………………………….(7分)
(2)证明:由(1)的结论可知:
当 时, 含峰区间的长度为
时, 含峰区间的长度为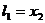 ;
;
当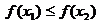 时, 含峰区间的长度为
时, 含峰区间的长度为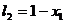 ;
;
对于上述两种情况,由题意得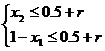 ①
①
由①得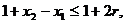 即
即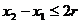 ,
,
又因为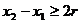 ,所以
,所以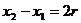 ②
②
将②代入①得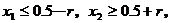 ③
③
由①和③解得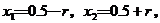
所以这时含峰区间的长度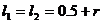 ,
,
即存在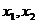 使得所确定的含峰区间的长度不大于
使得所确定的含峰区间的长度不大于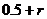 ………………………………(14分)
………………………………(14分)