
1. sin2100 =
(A)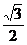 (B)
-
(B)
-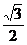 (C)
(C)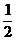 (D)
-
(D)
-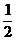
2.函数f(x)=|sinx|的一个单调递增区间是
(A)(- ,
, ) (B) (
) (B) ( ,
,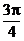 ) (C) (p,
) (C) (p,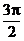 ) (D) (
) (D) (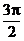 ,2p)
,2p)
3.设复数z满足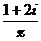 =i,则z =
=i,则z =
(A) -2+i (B) -2-i (C) 2-i (D) 2+i
4.以下四个数中的最大者是
(A) (ln2)2 (B)
ln(ln2) (C)
ln (D)
ln2
(D)
ln2
5.在∆ABC中,已知D是AB边上一点,若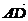 =2
=2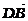 ,
,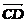 =
=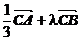 ,则l=
,则l=
(A)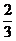 (B)
(B)
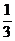 (C) -
(C) -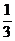 (D)
-
(D)
-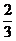
6.不等式: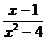 >0的解集为
>0的解集为
(A)( -2, 1) (B) ( 2, +∞)
(C) ( -2, 1)∪ ( 2, +∞) (D) ( -∞, -2)∪ ( 1, +∞)
7.已知正三棱柱ABC-A1B1C1的侧棱长与底面边长相等,则AB1与侧面ACC1A1所成角的正弦等于
(A) 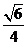 (B)
(B)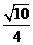 (C)
(C) 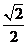 (D)
(D)
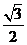
8.已知曲线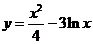 的一条切线的斜率为,则切点的横坐标为
的一条切线的斜率为,则切点的横坐标为
(A)3 (B) 2 (C) 1 (D)
9.把函数y=ex的图象按向量a=(2,3)平移,得到y=f(x)的图象,则f(x)=
(A) ex-3+2 (B) ex+3-2 (C) ex-2+3 (D) ex+2-3
10.从5位同学中选派4位同学在星期五、星期六、星期日参加公益活动,每人一天,要求星期五有2人参加,星期六、星期日各有1人参加,则不同的选派方法共有
(A)40种 (B) 60种 (C) 100种 (D) 120种
11.设F1,F2分别是双曲线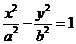 的左、右焦点。若双曲线上存在点A,使∠F1AF2=90º,且|AF1|=3|AF2|,则双曲线离心率为
的左、右焦点。若双曲线上存在点A,使∠F1AF2=90º,且|AF1|=3|AF2|,则双曲线离心率为
(A) 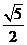 (B)
(B) 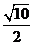 (C)
(C) 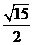 (D)
(D)
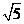
12.设F为抛物线y2=4x的焦点,A、B、C为该抛物线上三点,若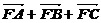 =0,则|FA|+|FB|+|FC|=
=0,则|FA|+|FB|+|FC|=
(A)9 (B) 6 (C) 4 (D) 3
第II卷(非选择题)
本卷共10题,共90分。
13.(1+2x2)(x-)8的展开式中常数项为 。(用数字作答)
14.在某项测量中,测量结果x服从正态分布N(1,s2)(s,0),若x在(0,1)内取值的概率为0.4,则x在(0,2)内取值的概率为 。
15.一个正四棱柱的各个顶点在一个直径为2cm的球面上。如果正四棱柱的底面边长为1cm,那么该棱柱的表面积为 cm2.
16.已知数列的通项an=-5n+2,其前n项和为Sn,则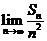 =
。
=
。
17.在 ∆ABC中,已知内角A=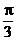 ,边 BC=2
,边 BC=2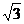 ,设内角B=x, 周长为y
,设内角B=x, 周长为y
(1)求函数y=f(x)的解析式和定义域;
(2)求y的最大值。
18. 从某批产品中,有放回地抽取产品二次,每次随机抽取1件,假设事件A:“取出的2件产品中至多有1件是二等品”的概率P(A)=0.96
(1)求从该批产品中任取1件是二等品的概率p;
(2)若该批产品共有100件,从中任意抽取2件,x表示取出的2件产品中二等品的件数,求x的分布列。
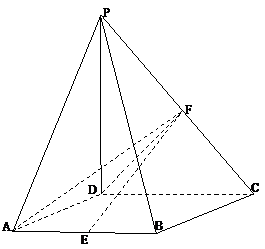
19.如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱
SD⊥ 底面ABCD,E、F分别是AB、SC的中点
(1) 求证:EF∥ 平面SAD
(2) 设SD = 2CD,求二面角A-EF-D的大小
20.在直角坐标系xOy中,以O为圆心的圆与直线:x-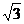 y=4相切
y=4相切
(1)求圆O的方程
(2)圆O与x轴相交于A、B两点,圆内的动点P使|PA|、|PO|、|PB|成等比数列,求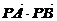 的取值范围。
的取值范围。
21.设数列{an}的首项a1∈ (0,1), an=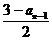 ,n=2,3,4…
,n=2,3,4…
(1)求{an}的通项公式;
(2)设 ,求证
,求证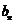 <
<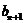 ,其中n为正整数。
,其中n为正整数。
22.已知函数f(x)=x3-x
(1)求曲线y=f(x)在点M(t,f(t))处的切线方程
(2)设a>0,如果过点(a,b)可作曲线y=f(x)的三条切线,证明:-a<b<f(a)
答案:DCCDACAACBBB