1.双曲线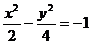 的渐近线方程为 ( )
的渐近线方程为 ( )
A.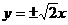 B.
B.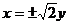 C.
C.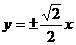 D.
D.
 2.设
2.设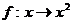 是集合A到集合B的映射,如果B={1,2},那么
是集合A到集合B的映射,如果B={1,2},那么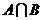 等于 ( )
等于 ( )
A. B.{1} C. 或{2} D. 或{1}
3.数列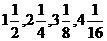 ,……的前n项和为 ( )
,……的前n项和为 ( )
A.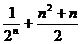 B.
B.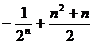
C.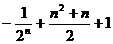 D.
D.
4.掷一个骰子的试验,事件A表示“小于5的偶数点出现”,事件B表示“小于5的点数出现”,则一次试验中,事件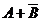 发生概率为 ( )
发生概率为 ( )
A.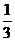 B.
B.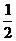 C.
C.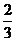 D.
D.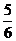
5.向量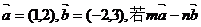 与
与 共线(其中
共线(其中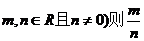 等于 ( )
等于 ( )
A.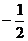 B.
B.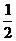 C.-2 D.2
C.-2 D.2
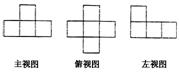 6.用若干块相同的小正方体搭成一个几何体,该几何体的三视图如下图所示,则搭成该几何体最少需要的小正方体的块数是 ( )
6.用若干块相同的小正方体搭成一个几何体,该几何体的三视图如下图所示,则搭成该几何体最少需要的小正方体的块数是 ( )
A.8 B.7
C.6 D.5
7.已知函数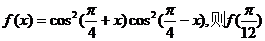 等于 (
)
等于 (
)
A.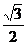 B.
B.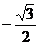 C.
C.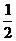 D.
D.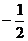
8.下列命题不正确的是(其中l,m表示直线,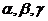 表示平面) ( )
表示平面) ( )
A.若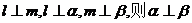 B.若
B.若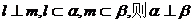
C.若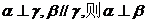 D.若
D.若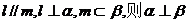
9.迄今为止,人类已借助“网格计算”技术找到了630万位的最大质数。小王发现由8个质数组成的数列41,43,47,53,61,71,83,97的一个通项公式,并根据通项公式得出数列的后几项,发现它们也是质数。小王欣喜万分,但小王按得出的通项公式,再往后写几个数发现它们不是质数。他写出不是质数的一个数是 ( )
A.1643 B.1679 C.1681 D.1697
 10.已知函数
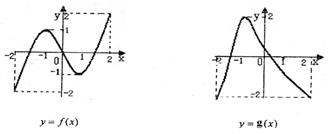
10.已知函数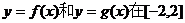 的图象如下所示
的图象如下所示
给出下列四个命题:
(1)方程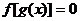 有且仅有6个根 (2)方程
有且仅有6个根 (2)方程 有且仅有3个根
有且仅有3个根
(3)方程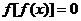 有且仅有5个根 (4)方程
有且仅有5个根 (4)方程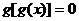 有且仅有4个根
有且仅有4个根
其中正确的命题个数是 ( )
A.4个 B.3个 C.2个 D.1个
11.函数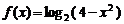 的定义域是_______________.
的定义域是_______________.
12.设直线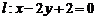 过椭圆的左焦
过椭圆的左焦
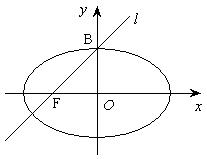 点F和一个顶点B(如图所示),则这个椭圆
点F和一个顶点B(如图所示),则这个椭圆
的离心率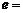 __________.
__________.
13.设平面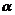 ∩平面
∩平面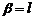 ,点
,点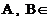 平面
平面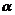 ,
,
点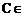 平面
平面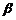 ,且三点A、B、C都不在直线l上,
,且三点A、B、C都不在直线l上,
给出下列四个命题:
① 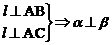 ②
② 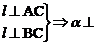 平面ABC ③
平面ABC ③ 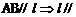 平面ABC
平面ABC
其中正确的命题是_______________.
▲选做题:在下面二道小题中选做一题,两题都选的只计算第一题的得分.
14.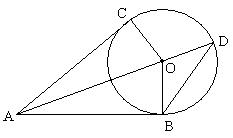 如图所示,AC和AB分别是圆O的切线,
如图所示,AC和AB分别是圆O的切线,
且OC = 3,AB = 4,延长OA到D点,则△ABD的
面积是___________.
15.在极坐标系中,点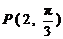 到直线
到直线
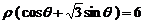 的距离是___________.
的距离是___________.
16.(本小题满分12分)在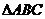 中,已知
中,已知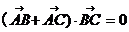 ,
,
(1) 求证: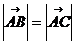 ;
;
(2)若 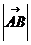 =2,
=2,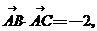 求
求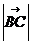
17、(本小题满分14分)如图,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面所成的角为45°,底面ABCD为直角梯形,∠ABC = ∠BAD = 90°,PA = BC = AD.
(Ⅰ)求证:平面PAC⊥平面PCD;
 (Ⅱ)在棱PD上是否存在一点E,使CE∥平面PAB ?若存在,请确定E点的位置;若不存在,请说明理由.
(Ⅱ)在棱PD上是否存在一点E,使CE∥平面PAB ?若存在,请确定E点的位置;若不存在,请说明理由.
18.(本小题满分14分)某工厂生产甲、乙两种产品,已知生产每吨甲、乙两种产品所需煤、电力、劳动力、获得利润及每天资源限额(最大供应量)如下表所示:
 产品
产品消耗量 资源 |
甲产品 (每吨) |
乙产品 (每吨) |
资源限额 (每天) |
|
煤(t) |
9 |
4 |
360 |
|
电力(kw.h) |
4 |
5 |
200 |
|
劳力(个) |
3 |
10 |
300 |
|
利润(万元) |
6 |
12 |
|
问:每天生产甲、乙两种产品各多少吨,获得利润总额最大?
19.(本小题满分14分)已知函数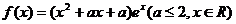
(Ⅰ)当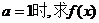 的单调区间;
的单调区间;
(Ⅱ)是否存在实数a,使f(x)的极大值为3?若存在,求出a的值,若不存在,请说明理由。
20.(本小题满分14分)已知M(4,0)、N(1,0),若动点P满足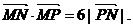
(Ⅰ)求动点P的轨迹C的方程;
(Ⅱ)设过点N的直线l交轨迹C于A、B两点,若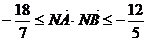 ,求直线l的斜率的取值范围。
,求直线l的斜率的取值范围。
 21(本小题满分12分)
21(本小题满分12分)
如图所示,设非负实数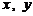 满足不等
满足不等
式组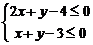 .
.
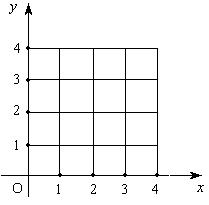
(Ⅰ)在所给坐标系中画出不等式组所表示的平面区域;
(Ⅱ)求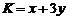 的最大值;
的最大值;
(Ⅲ)若在不等式组所表示的平面区域散点,求该点落
在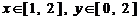 区域内的概率.
区域内的概率.
08届高考数学水平测试试题
08届高考数学水平测试试题 数学(文)试题 本卷分为选择题和非选择题两部分,满分150分,考试时间120分钟。参考答案
数学(文)试题答案
一.选择题答案:1-5 ADCCA 6-10 BDBCB
二. 填空题: 本大题共4小题,每小题5分,共20分. 把正确答案填在题中横线上.
(11)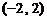 (12)
(12)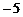 (13)
(13)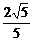 (14)②③ (15)
(14)②③ (15) (16)1
(16)1
16.
(I)证明: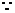
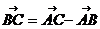 , ……………………………..(2分)
, ……………………………..(2分)
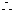
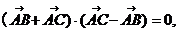
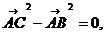 ………………………………(4分)
………………………………(4分)
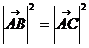 故
故 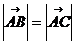 ……………(6分)
……………(6分)
(2)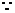
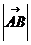 =2,
=2,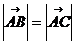 ,
, 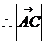 =2
又
=2
又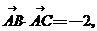
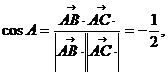 ………………………………….(10分)
………………………………….(10分)
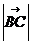 =
=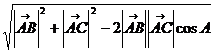 =
=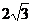 …………..(12分)
…………..(12分)
17、解:设PA = 1.
(Ⅰ)由题意 PA = BC = 1, AD = 2. …………………………………… 2分
∵ PA⊥面ABCD,∴ PB与面ABCD所成的角为∠PBA = 45°.
∴ AB = 1,由∠ABC = ∠BAD = 90°,易得CD = AC = .
由勾股定理逆定理得 AC⊥CD. …………………………………… 3分
又∵ PA⊥CD, PA∩AC = A,∴ CD⊥面PAC, …………………………………… 5分
又CD Ì 面PCD,
∴ 面PAC⊥面PCD. …………………………………… 6分
(Ⅱ)分别以AB, AD, AP所在直线分别为x轴, y轴, z轴建立空间直角坐标系.
∴ P(0, 0, 1), C(1, 1, 0), D(0, 2, 0). …………………………………… 8分
 |
设E(0, y, z),则= (0, y, z-1), = (0, 2, -1). …………………………………… 9分
∵ ∥,∴ y.(-1)-2 (z-1) = 0 … ① …………………………………… 10分
= (0, 2, 0) 是平面PAB的法向量, …………………………………… 11分
又 = (-1, y-1, z),由CE∥面PAB,∴ ⊥. …………………………… 12分
∴ (-1, y-1, z).(0, 1, 0) = 0,∴ y = 1,代入得z = . …………………………………13分
∴ E是PD中点,∴ 存在E点使得CE∥面PAB. …………………………………… 14分
18.解:设此工厂应分别生产甲、乙两种产品x吨y吨,获得利润z万元…………1分
|
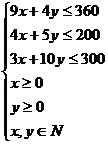 …………………………5分
…………………………5分
(图2分)
利润目标函数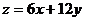 ………………………………8分
………………………………8分
如图,作出可行域,作直线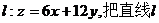 向右上方平移至l1位置,直线经过可行域上的点M,且与原点距离最大,此时
向右上方平移至l1位置,直线经过可行域上的点M,且与原点距离最大,此时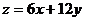 取最大值。……10分
取最大值。……10分
解方程组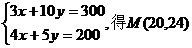 ………………………………12分
………………………………12分
所以生产甲种产品20t,乙种产品24t,才能使此工厂获得最大利润。……14分
19.解:(Ⅰ)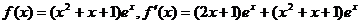
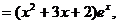 ………………………………………………………………3分
………………………………………………………………3分
当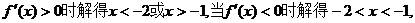
所以函数的单调增区间为(-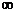 ,-3),(-1,+
,-3),(-1,+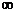 );
);
单调减区产为(-3,-1)………………………………6分)
(Ⅱ)
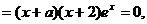 ……………………8分
……………………8分
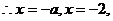
列表如下: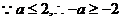 ……………………………………加表格12分
……………………………………加表格12分
|
x |
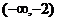 |
-2 |
(-2,-a) |
-a |
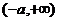 |
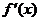 |
+ |
0 |
- |
0 |
+ |
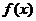 |
 |
极大 |
 |
极小 |
 |
由表可知 解得
解得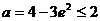 ,所以存在实数a,使
,所以存在实数a,使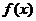 的极大值为3。………………………………………………14分
的极大值为3。………………………………………………14分
20.解答:(1)设动点P(x,y),
则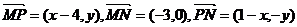 …………………………2分
…………………………2分
由已知得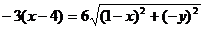 ,化简得
,化简得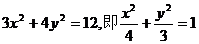
∴点P的轨迹是椭圆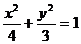 ……………………………………6分
……………………………………6分
(Ⅱ)设过N的直线l的方程为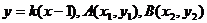
由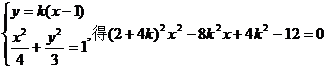 …………………………8分
…………………………8分
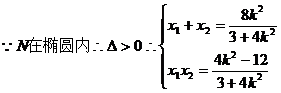 …………………………10分
…………………………10分
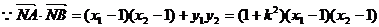
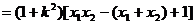
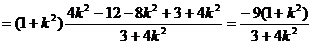 ……………………12分
……………………12分
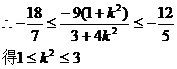
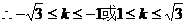 …………………………………………14分
…………………………………………14分
21.(Ⅰ)略;(Ⅱ)9;(Ⅲ)