
1.设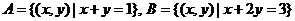 满足C
满足C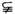
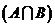 的集合C的个数为
的集合C的个数为
(A)0 (B)1 (C)2 (D)4
2. 已知函数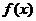 有反函数
有反函数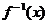 ,且函数
,且函数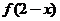 的图象过点(1,3),则函数
的图象过点(1,3),则函数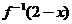 的图象必过点
的图象必过点
(A)(1,3) (B)(3,1) (C) 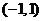 (D)(1,1)
(D)(1,1)
3.若复数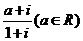 是纯虚数,则实数
是纯虚数,则实数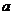 的值为
的值为
(A)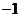 (B)
(B)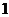 (C)
(C)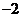 (D)
(D)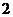
4.已知条件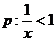 ,条件
,条件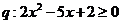 ,若
,若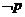 和
和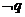 中有且只有一个成立,则
中有且只有一个成立,则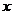 的取值范围是
的取值范围是
(A) (B)
(B)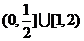 (C)
(C)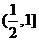 (D)
(D)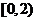
5.下列命题不正确的是(其中l,m表示直线,α,β, r表示平面) ( )
A.若l⊥m,l⊥α,m⊥β,则α⊥β B.若l⊥m,l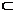 α,m
α,m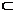 β,则α⊥β
β,则α⊥β
C.若α⊥r,β//r,则α⊥β D.若l//m,l⊥α,m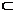 β,则α⊥β
β,则α⊥β
6.6人排成一排,要求甲、乙两人中间恰好有1人,且甲,乙都不与丙相邻,则不同的排列
方法有 ( )
A.24 B.72 C.48 D.36
7.已知F1,F2是双曲线 的左右焦点,过F1作垂直于x轴的直线
的左右焦点,过F1作垂直于x轴的直线
交双曲线于A、B两点,若△ABF2为锐角三角形,则双曲线离心率的取值范围是( )
A.(1,1+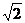 ) B.(1+
) B.(1+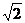 ,+∞) C.(1-
,+∞) C.(1-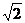 ,1+
,1+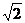 )D.(
)D.(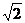 ,
,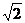 +1)
+1)
|
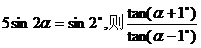 的值是 ( )
的值是 ( )
A.-2 B.-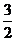 C.
C.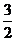 D.2
D.2
9.正四面体的内切球,与各棱都相切的球,外接球的半径之比为 ( )
A.1: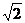 :
: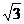 B.1:
B.1: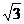 :3 C.1:
:3 C.1: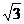 :2 D.1:2:3
:2 D.1:2:3
10.函数f(x)=x2-2ax+a在区间(-∞,1)上有最小值,则函数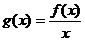 在区间(1,
在区间(1,
+∞)上一定 ( )
A.有最小值 B.有最大值 C.是减函数 D.是增函数
第Ⅱ卷
11.在由正数组成的等比数列{an}中,a1+a2=1,a3+a4=4,则a4+a5=_________
12.设f(x)=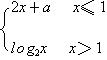 ,若
,若 f (x)存在,则常数a=___________
f (x)存在,则常数a=___________
13.已知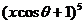 的展开式中x2的系数与
的展开式中x2的系数与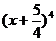 的展开式中x3的二项式系数相等,则cosθ=
.
的展开式中x3的二项式系数相等,则cosθ=
.
 14.当x,y满足条件
14.当x,y满足条件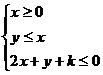 (k为常数)时,能使Z=x+3y的最大值为12的k的值是
.
(k为常数)时,能使Z=x+3y的最大值为12的k的值是
.
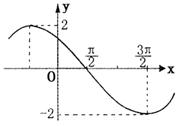
15.已知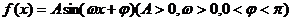
其导函数f′(x)的图象(部分)如图,则f(x)的解析式
为 .
16.已知定义在R上的函数f(x)的图象关于点(-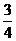 ,0)成为中心对称图形,且满足
,0)成为中心对称图形,且满足
 的值为 .
的值为 .
17.(本小题满分13分)
(本题满分12分)已知锐角△ABC三个内角为A、B、C,向量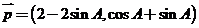 与向量
与向量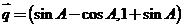 是共线向量.
是共线向量.
①求角A.②求函数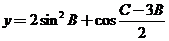 的最大值.
的最大值.
18.(本小题满分13分)一个口袋里面装有2个白球4个黑球,这些球除颜色差别外没有其它的区别. 现在从袋中随机取出一个来记好颜色,然后放回并搅匀,之后再随机取球记色,再放回搅匀,…. 记数列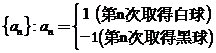 ,数列
,数列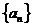 的前n项和记为
的前n项和记为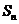 ①.求事件“
①.求事件“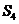 =2”的概率; ②求
=2”的概率; ②求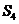 取值的分布列和数学期望
取值的分布列和数学期望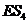 .
.
19.(本小题满分13分)如图,正方形ABCD中,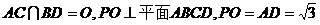 ,点E在PD上,PE:ED=2:1。
,点E在PD上,PE:ED=2:1。
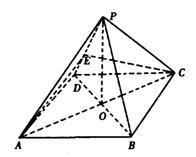 (1)证明:PD⊥平面EAC;
(1)证明:PD⊥平面EAC;
(2)求二面角A-PD-C的余弦值;
(3)求点B到平面PDC的距离。
20.(本小题满分13分)
已知函数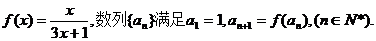
(1)求数列{an}的通项an;
(2)若数列{bn}的前n项和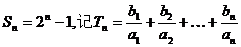 求Tn.
求Tn.
21.(本小题满分12分)
设函数y=f(x)=x(x-a)(x-b) (a,b∈R)
(1)a≠b,ab≠0,过两点(0,0),(a,0)的中点作与x轴垂直的直线与函数y=f(x)的图象交于点P(x0,f(x0)),求证:函数y=f(x)在点P处的切线经过点(b,0);
(2)若a=b(a≠0)且当x∈[0,|a|+1]时,f(x)<2a2恒成立,求实数a的取值范围 。
22.(本小题满分12分)
 如图:已知椭圆
如图:已知椭圆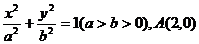 是长轴的一个端点,弦BC过椭圆的中心O,且
是长轴的一个端点,弦BC过椭圆的中心O,且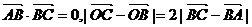 .
.
(1)求椭圆的方程;
(2)若AB上的一点F满足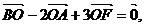
求证:CF平分∠BCA;
(3)对于椭圆上的两点P、Q,∠PCQ的平分线总是垂直于x轴时,是否存在实数λ,使得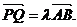
高考预测理科数学试卷 参考公式: 如果事件A、B互斥,那么 球的表面积公式 P(A+B)=P(A)+P(B) S=4πR2 如果事件A、B相互独立, 其中R表示球的半径 那么P(A.B)=P(A).P(B) 球的体积公式 如果事件A在一次试验中发生的概率 是P,那么n次独立重复试验中恰好发 其中R表示球的半径 生k 次的概率P参考答案
参考答案
一、选择题:
1-5BCAAB 6-10BABBD 11-12AC
二、填空题:
11.8
12.-2 13.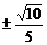 14.-9 15.
14.-9 15.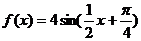 16.1
16.1
三、解答题:
17.解:(1)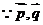 共线
共线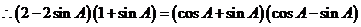 …….2’
…….2’
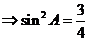 ……………2’ 而
……………2’ 而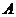 为锐角,所以
为锐角,所以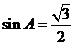
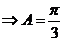 …...2’
…...2’
(2)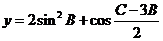
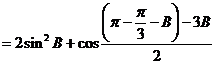
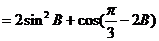
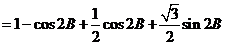
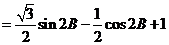
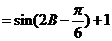 …………..3’
…………..3’
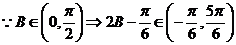
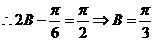 时,
时,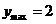 ………….4’
………….4’
18.解:(1)事件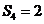 只能是“四次取球中出现三次白球一次黑球”,
只能是“四次取球中出现三次白球一次黑球”,
每次取得白球的概率为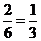 ;取得黑球的概率是
;取得黑球的概率是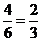 …………..2’
…………..2’
于是 ………………………………..2’
………………………………..2’
(2)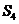 可能的取值有
可能的取值有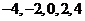
 ;
;
 ;
;
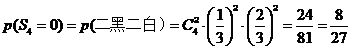 ;
;
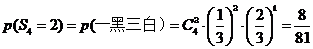 ;
;
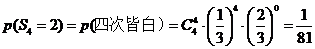 ,…………………5’
,…………………5’
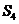 |
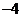 |
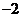 |
0 |
2 |
4 |
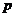 |
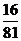 |
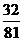 |
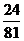 |
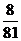 |
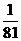 |
于是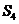 取值的分布列为
取值的分布列为
………………………………………….2’
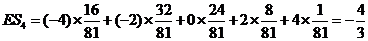 …………2’
…………2’
19.(1)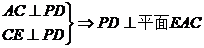
(2)∠CEA为二面角A-PD-C的平面角,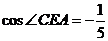
(3)点B到平面PDC的距离为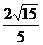
20.解:(1)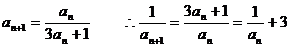
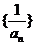 是首项a1,公差d=3的等差数列
是首项a1,公差d=3的等差数列
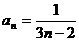
(2)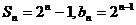
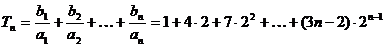
2Tn=1.2+4.22+7.22+…+(3n-2).2n
两式相减-Tn=1+3(2+22+…+2n-1)-(3n-2).2n
=-5-(3n-5).2n
∴Tn=(3n-5).2n+5
21.解:(1)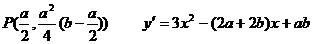
所求切线斜率为 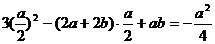
切线 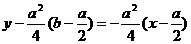
令y=0 得x=b ∴函数y=f(x)过点P的切线过点(b,0)
(2)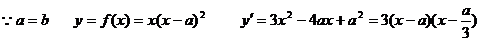
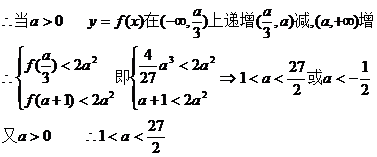
当a<0时,函数y=f(x)在(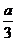 ,+∞)上递增
,+∞)上递增
∴f(1-a)<2a2.即(1-a)(1-a-a)2<2a2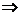 4a3-6a2+5a-1>0
4a3-6a2+5a-1>0
令g(a)=4a3-ba2+5a-1
g′(a)=12a2-12a+5=12(a-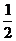 )2+2>0
)2+2>0
∴g(a)在(-∞,0)单增 又g(0)=-1<0 ∴g(a)>0无解
综上 1<a<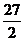
22.(I)解: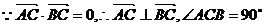
又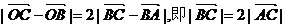
∴△AOC是等腰直角三角形
∵A(2,0),∴C(1,1)而点C在椭圆上,
∴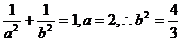
∴所求椭圆方程为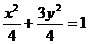
(Ⅱ)证明C(1,1),则B(-1,-1)
又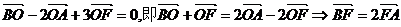
即点F分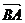 所成的定比为2.
所成的定比为2.
设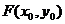
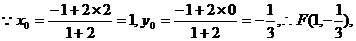
CF⊥x轴,
∴∠ACF=∠FCB=45°,即CF平分∠BCA.
(Ⅲ)对于椭圆上两点P、Q,∵∠PCQ的平分线总是垂直于x轴
∴PC与CQ所在直线关于x=1对称,kpC=k,则kcQ=-k,
设C(1,1),则PC的直线方程y-1=k(x-1)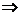 y=k(x-1)+1
①
y=k(x-1)+1
①
QC的直线方y-1=-k(x-1) 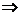 y=-k(x-1)+1 ②
y=-k(x-1)+1 ②
将①代入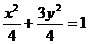 得(1+3k2)x2-6k(k-1)x+3k2-6k-1=0 ③
得(1+3k2)x2-6k(k-1)x+3k2-6k-1=0 ③
∵C(1,1)在椭圆上,∴x=1是方程③的一个根,
∴xp.1=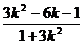 =1同理将②代入x2+3y2=4得
=1同理将②代入x2+3y2=4得
(1+3k2)x2-6k(k+1)x+3k2+6k-1=0 ④
∵C(1,1)在椭圆上,
∴x=1是方程④的一个根,
∴xQ.1= 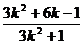
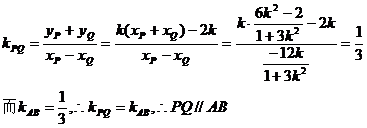
∴存在实数λ,使得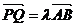 .
.