
1. 已知 为实数集,
为实数集,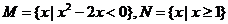 ,则
,则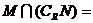 ( ).
( ).
A.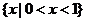 B.
B.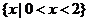 C.
C.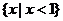 D.
D.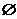
2. 若复数
若复数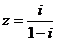 ,则
,则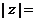 ( ).
( ).
A.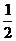 B.
B.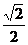 C.1
D.
C.1
D.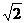
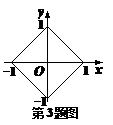
3. 设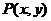 是图中的四边形内的点或四边形边界上的点,则
是图中的四边形内的点或四边形边界上的点,则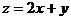 的最大值是( ).
的最大值是( ).
 A.
A.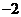 B.
B.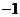 C.
C.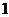 D.
D.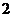
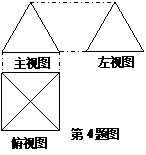
4. 如图,一个简单空间几何体的三视图其主视图与左视图是边长为2的正三角形、俯视图轮廓为正方形,则其体积是( ).
A.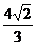 B .
B . 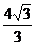 C.
C.
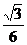 D .
D . 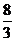
5. 设a、b、c分别是△ABC中∠A、∠B、∠C所对边的边长,则直线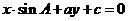 与
与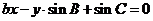 的位置关系是(
).
的位置关系是(
).
A.平行 B.重合 C.垂直 D.相交但不垂直
6. 如图,圆弧型声波DFE从坐标原点O向外传播. 若D是DFE弧与x 轴的交点,设OD = x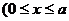 ),圆弧型声波DFE在传播过程中扫过平行四边形OABC的面积为
),圆弧型声波DFE在传播过程中扫过平行四边形OABC的面积为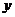 (图中阴影部分),则函数
(图中阴影部分),则函数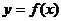 的图象大致是( ).
的图象大致是( ).
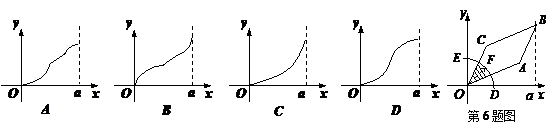
7.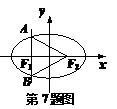 已知点F1、F2分别是椭圆
已知点F1、F2分别是椭圆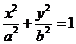 的左、右焦点,过F1且垂直于x轴的直线与椭圆交于A、B两点,若△ABF2为正三角形,则该椭圆的离心率
的左、右焦点,过F1且垂直于x轴的直线与椭圆交于A、B两点,若△ABF2为正三角形,则该椭圆的离心率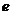 是( ).
是( ).
A.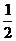 B.
B. 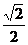 C.
C. 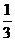 D.
D. 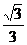
8. 已知函数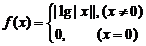 ,则方程
,则方程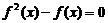 的实根共有( ).
的实根共有( ).
A.5个 B.6个 C.7个 D.8个
9. 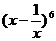 的展开式中的常数项是
(用数字作答).
的展开式中的常数项是
(用数字作答).
10.用一根长为12m的铝合金条做成一个“目”字形窗户的框架(不计损耗),要使这个窗户通过的阳光最充足,则框架的长与宽应为 .
11.函数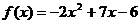 与
与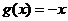 的图象所围成封闭图形的面积为 .
的图象所围成封闭图形的面积为 .
12.考察下列一组不等式:
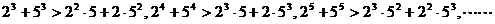 .
.
 将上述不等式在左右两端仍为两项和的情况下加以推广,使以上的不等式成为推广不等式的特例,则推广的不等式可以是___________________.
将上述不等式在左右两端仍为两项和的情况下加以推广,使以上的不等式成为推广不等式的特例,则推广的不等式可以是___________________.
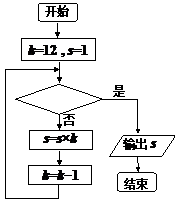
13.若框图所给的程序运行的结果为S=132,那么判断框中
应填入的关于k的判断条件是 .
14. 等差数列
等差数列 的前
的前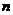 项和为
项和为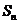 ,公差
,公差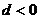 . 若存在正整数
. 若存在正整数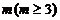 ,使得
,使得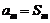 ,则当
,则当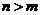 (
(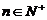 )时,有
)时,有 (填“>”、“<”、“=”).
(填“>”、“<”、“=”).
15.(本小题满分12分)
已知: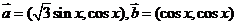 ,
,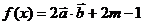 (
(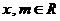 ).
).
(1) 求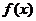 关于
关于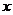 的表达式,并求
的表达式,并求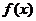 的最小正周期;
的最小正周期;
(2) 若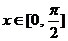 时
时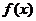 的最小值为5,求
的最小值为5,求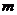 的值.
的值.
16.(本小题满分12分)
如图,四边形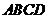 为矩形,且
为矩形,且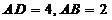 ,
,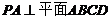 ,
,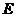 为
为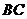 上的动点.
上的动点.
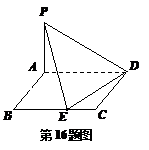 (1) 当
(1) 当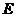 为
为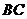 的中点时,求证:
的中点时,求证: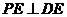 ;
;
(2) 设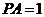 ,在线段
,在线段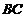 上存在这样的点E,使得二面角
上存在这样的点E,使得二面角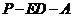 的大小为
的大小为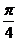 . 试确定点E的位置.
. 试确定点E的位置.
17、(本小题满分14分)
设数列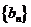 的前
的前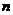 项和为
项和为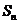 ,且
,且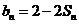 ;数列
;数列 为等差数列,且
为等差数列,且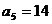 ,
,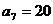 .
.
(1) 求数列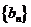 的通项公式;
的通项公式;
(2) 若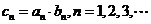 ,
,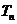 为数列
为数列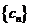 的前
的前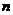 项和. 求证:
项和. 求证: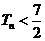 .
.
18.(本小题满分14分)
已知动圆过定点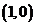 ,且与直线
,且与直线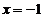 相切.
相切.
(1) 求动圆的圆心轨迹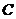 的方程;
的方程;
(2) 是否存在直线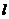 ,使
,使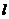 过点(0,1),并与轨迹
过点(0,1),并与轨迹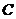 交于
交于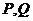 两点,且满足
两点,且满足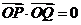 ?若存在,求出直线
?若存在,求出直线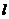 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
19.(本小题满分14分)
为了对2006年佛山市中考成绩进行分析,在60分以上的全体同学中随机抽出8位,他们的数学分数(已折算为百分制)从小到大排是60、65、70、 75、80、85、 90、95,物理分数从小到大排是72、 77、 80、84、88、90、93、95.
(1) 若规定85分(包括85分)以上为优秀,求这8位同学中恰有3位同学的数学和物理分数均为优秀的概率;
(2) 若这8位同学的数学、物理、化学分数事实上对应如下表:
|
学生编号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
数学分数x |
60 |
65 |
70 |
75 |
80 |
85 |
90 |
95 |
|
物理分数y |
72 |
77 |
80 |
84 |
88 |
90 |
93 |
95 |
|
化学分数z |
67 |
72 |
76 |
80 |
84 |
87 |
90 |
92 |
(2) 用变量y与x、z与x的相关系数说明物理与数学、化学与数学的相关程度;
(3) 求y与x、z与x的线性回归方程(系数精确到0.01),并用相关指数比较所求回归模型的效果.
参考数据: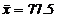 ,
,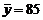 ,
,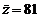 ,
,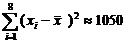 ,
,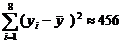 ,
,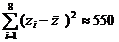 ,
,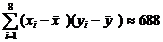 ,
, ,
,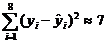
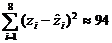 ,
,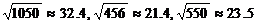 .
.
20.(本小题满分14分)
已知函数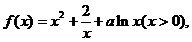
(1) 若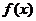 在
在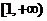 上单调递增,求
上单调递增,求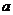 的取值范围;
的取值范围;
(2) 若定义在区间D上的函数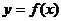 对于区间D上的任意两个值
对于区间D上的任意两个值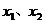 总有以下不等式
总有以下不等式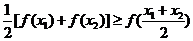 成立,则称函数
成立,则称函数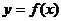 为区间D上的“凹函数”.
为区间D上的“凹函数”.
试证当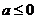 时,
时,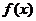 为“凹函数”.
为“凹函数”.
高考理科数学模拟试题(理科1)参考答案
数学试题参考答案和评分标准(理科1)
一、选择题(每题5分,共40分)
|
序号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
答案 |
A |
B |
D |
B |
C |
A |
D |
C |
二、填空题(每题5分,共30分)
9.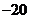 .
10.3m与1.5m. 11.
.
10.3m与1.5m. 11.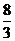 .
.
12.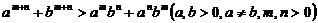 (或
(或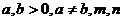 为正整数).注:填
为正整数).注:填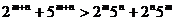 以及是否注明字母的取值符号和关系,均不扣分;
以及是否注明字母的取值符号和关系,均不扣分;
若填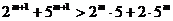 或
或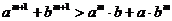 可给3分.
可给3分.
13.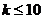 . 14.<.
. 14.<.
三、解答题(本大题共6小题,共80分)
15. 解:(1) 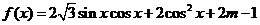 ……………………………………………………2分
……………………………………………………2分
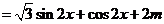 ………………………………………………………………………………………………4分
………………………………………………………………………………………………4分
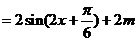 . …………………………………………………………………………………………………………6分
. …………………………………………………………………………………………………………6分
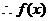 的最小正周期是
的最小正周期是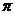 . …………………………………………………………………………………………………7分
. …………………………………………………………………………………………………7分
(2) ∵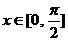 ,∴
,∴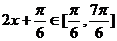 …………………………………………………………………8分
…………………………………………………………………8分
∴当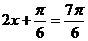 即
即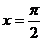 时,函数
时,函数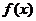 取得最小值是
取得最小值是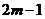 . ………………………10分
. ………………………10分
∵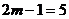 ,∴
,∴ . …………………………………………………………………………………………………12分
. …………………………………………………………………………………………………12分
16. 方法一:(2) 证明:当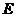 为
为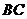 中点时,
中点时, ,从而
,从而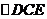 为等腰直角三角形,则
为等腰直角三角形,则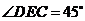 ,同理可得
,同理可得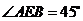 ,∴
,∴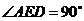 ,于是
,于是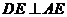 ,…2分
,…2分
又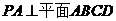 ,且
,且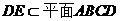 ,∴
,∴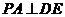 ,…………………………………………4分
,…………………………………………4分
∴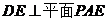 ,又
,又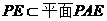 ,∴
,∴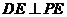 . …………………………………………………6分
. …………………………………………………6分
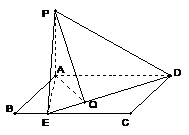 (也可以利用三垂线定理证明,但必需指明三垂线定理)
(也可以利用三垂线定理证明,但必需指明三垂线定理)
(2) 如图过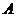 作
作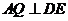 于
于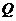 ,连
,连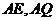 ,则
,则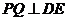 ,
,
∴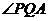 为二面角
为二面角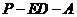 的平面角. ………8分
的平面角. ………8分
设 ,则
,则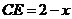 .
.
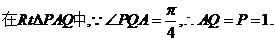
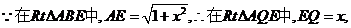
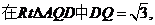 于是
于是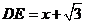 …………………………………………………………10分
…………………………………………………………10分
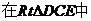 ,有
,有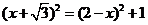
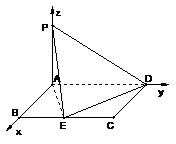 解之得
解之得 。
。
点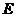 在线段BC上距B点的
在线段BC上距B点的 处. …………………………………………………………………………12分
处. …………………………………………………………………………12分
方法二、向量方法.以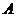 为原点,
为原点,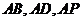 所在直线为
所在直线为
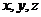 轴,建立空间直角坐标系,如图. …………………………1分
轴,建立空间直角坐标系,如图. …………………………1分
(1)不妨设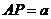 ,则
,则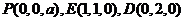 ,
,
从而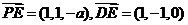 ,………………………4分
,………………………4分
于是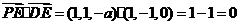 ,
,
所以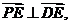 所以
所以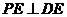 …………………………………………………………………………………6分
…………………………………………………………………………………6分
(2)设 ,则
,则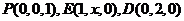 ,
,
则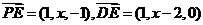 .………………………………………………………………………………8分
.………………………………………………………………………………8分
易知向量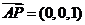 为平面
为平面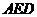 的一个法向量.设平面
的一个法向量.设平面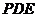 的法向量为
的法向量为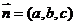 ,则应有
,则应有
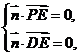 即
即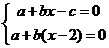 解之得
解之得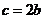 ,令
,令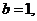 则
则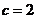 ,
,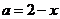 ,
,
从而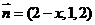 ,………………………………………………………………………………………………………10分
,………………………………………………………………………………………………………10分
依题意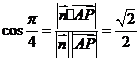 ,即
,即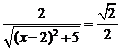 ,解之得
,解之得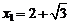 (舍去),
(舍去),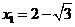
所以点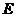 在线段BC上距B点的
在线段BC上距B点的 处.…………………………………………………………………12分
处.…………………………………………………………………12分
17. 解:(1)由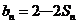 ,令
,令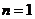 ,则
,则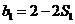 ,又
,又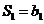 ,所以
,所以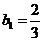 .
.
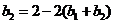 ,则
,则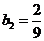 . ……………………………………………………………………………………2分
. ……………………………………………………………………………………2分
当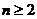 时,由
时,由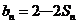 ,可得
,可得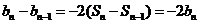 .
.
即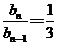 . …………………………………………………………………………………………………………………………4分
. …………………………………………………………………………………………………………………………4分
所以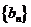 是以
是以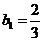 为首项,
为首项,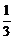 为公比的等比数列,于是
为公比的等比数列,于是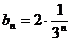 . …………5分
. …………5分
(2)数列 为等差数列,公差
为等差数列,公差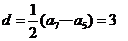 ,可得
,可得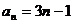 . ………………7分
. ………………7分
从而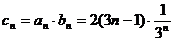 .
……………………………………………………………………………………8分
.
……………………………………………………………………………………8分
∴ ……………10分
……………10分
∴ .
…………………11分
.
…………………11分
从而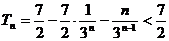 .
…………………………………………………………………………14分
.
…………………………………………………………………………14分
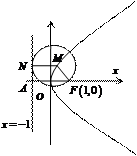 18.(1)如图,设
18.(1)如图,设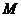 为动圆圆心,
为动圆圆心, 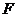
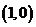 ,过点
,过点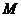 作直线
作直线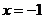 的垂线,垂足为
的垂线,垂足为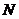 ,由题意知:
,由题意知: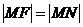 , ………………………………………………2分
, ………………………………………………2分
即动点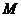 到定点
到定点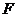 与定直线
与定直线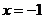 的距离相等,由抛物线的定义知,点
的距离相等,由抛物线的定义知,点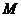 的轨迹为抛物线,其中
的轨迹为抛物线,其中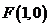 为焦点,
为焦点,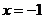 为准线, ∴ 动点
为准线, ∴ 动点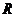 的轨迹方程为
的轨迹方程为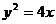 ………………………5分
………………………5分
(2)由题可设直线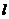 的方程为
的方程为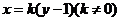 ,
,
由 得
得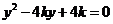
△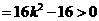 ,
,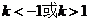 ………………………………………………………………………………7分
………………………………………………………………………………7分
设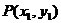 ,
,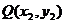 ,则
,则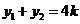 ,
,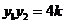 ……………………………………………9分
……………………………………………9分
由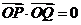 ,即
,即 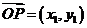 ,
,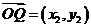 ,于是
,于是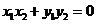 ,……11分
,……11分
即 ,
,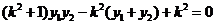 ,
,
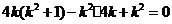 ,解得
,解得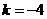 或
或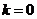 (舍去),…………………………………13分
(舍去),…………………………………13分
又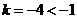 , ∴ 直线
, ∴ 直线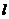 存在,其方程为
存在,其方程为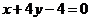 ………………………………………14分
………………………………………14分
19. 解:(1)这8位同学中恰有3位同学的数学和物理分数均为优秀,则需要先从物理的4个优秀分数中选出3个与数学优秀分数对应,种数是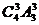 (或
(或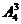 ),然后将剩下的5个数学分数和物理分数任意对应,种数是
),然后将剩下的5个数学分数和物理分数任意对应,种数是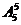 。根据乘法原理,满足条件的种数是
。根据乘法原理,满足条件的种数是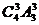
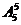 。 …………………………………………………………………………………………………………………………………4分
。 …………………………………………………………………………………………………………………………………4分
这8位同学的物理分数和数学分数分别对应的种数共有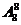 。 ………………………………5分
。 ………………………………5分
故所求的概率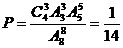 . ………………………………………………………………………………6分
. ………………………………………………………………………………6分
(2) 变量y与x、z与x的相关系数分别是
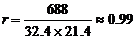 、
、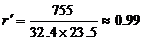 .
.
可以看出,物理与数学、化学与数学的成绩都是高度正相关. …………………………8分
(3) 设y与x、z与x的线性回归方程分别是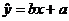 、
、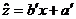 .
.
根据所给的数据,可以计算出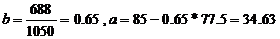 ,
,
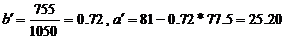 . ……………………………………………………10分
. ……………………………………………………10分
所以y与x和z与x的回归方程分别是
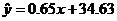 、
、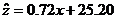 . …………………………………………………………11分
. …………………………………………………………11分
又y与x、z与x的相关指数是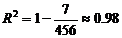 、
、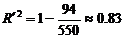 . ……13分
. ……13分
故回归模型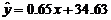 比回归模型
比回归模型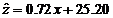 的拟合的效果好. …14分
的拟合的效果好. …14分
20. (Ⅰ)由 ,得
,得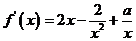 ……………………………………2分
……………………………………2分
函数为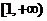 上单调函数. 若函数为
上单调函数. 若函数为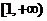 上单调增函数,则
上单调增函数,则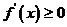 在
在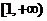 上恒成立,即不等式
上恒成立,即不等式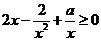 在
在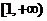 上恒成立. 也即
上恒成立. 也即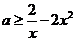 在
在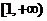 上恒成立. ……………………………………………………………………………………………………………………………………………4分
上恒成立. ……………………………………………………………………………………………………………………………………………4分
令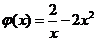 ,上述问题等价于
,上述问题等价于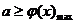 ,而
,而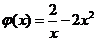 为在
为在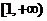 上的减函数,则
上的减函数,则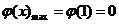 ,于是
,于是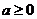 为所求. …………………………………………………………6分
为所求. …………………………………………………………6分
(Ⅱ)证明:由 得
得
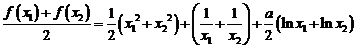
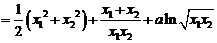 ……………………………………………………………………………7分
……………………………………………………………………………7分
 ………………………………………………………………8分
………………………………………………………………8分
而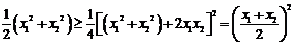 ① ………………………………………10分
① ………………………………………10分
又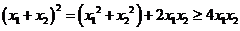 , ∴
, ∴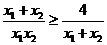 ② …………11分
② …………11分
∵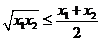 ∴
∴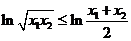 ,
,
∵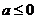 ∴
∴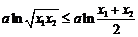 ③ ……………………………………………………………………13分
③ ……………………………………………………………………13分
由①、②、③得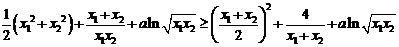
即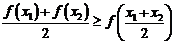 ,从而由凹函数的定义可知函数为凹函数. …………14分
,从而由凹函数的定义可知函数为凹函数. …………14分