
1、已知集合M={y| y=x+1},N={(x,y)|x 2 +y 2 =1},则M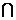 N中元素的个数是
N中元素的个数是
A.0 B.1 C.2 D.多个
2、已知复数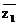 =a+i,z2=1+a 2 i,若
=a+i,z2=1+a 2 i,若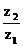 是实数,则实数a的值等于
是实数,则实数a的值等于
A.1 B.-1 C.-2 D.2
3、若函数f (x)= e xsin x,则此函数图象在点(4,f (4))处的切线的倾斜角为
A.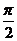 B.0 C.钝角 D.锐角
B.0 C.钝角 D.锐角
4、连掷两次骰子分别得到点数m、n,则向量(m,n)与向量(-1,1)的夹角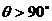 的概率是
的概率是
A.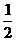 B.
B.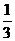 C.
C.  D.
D. 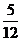
5、平面向量也叫二维向量,二维向量的坐标表示及其运算可以推广到n(n≥3)维向量,
n维向量可用(x1,x2,x3,x4,…,xn)表示.设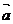 =(a1,
a2, a3, a4,…, an),
=(a1,
a2, a3, a4,…, an),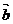 =(b1,
b2, b3, b4,…,bn),
=(b1,
b2, b3, b4,…,bn),
规定向量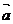 与
与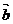 夹角θ的余弦为
夹角θ的余弦为
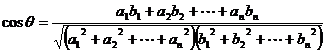 。
。
当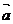 =(1,1,1,1,…,1),
=(1,1,1,1,…,1),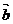 =(-1, -1, 1, 1,…,1)时,
=(-1, -1, 1, 1,…,1)时,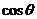 =
=
A、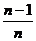 B、
B、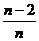 C、
C、 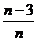 D、
D、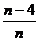
6、函数f (x)为奇函数且f (3x+1)的周期为3,f (1)=-1,则f (2006)等于
A.0 B.1 C.一1 D.2
7、在一个锥体中,作平行于底面的截面,若这个截面面积与底面面积之比为1∶3,则
锥体被截面所分成的两部分的体积之比为( )
A.1∶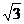 B.1∶9 C.1∶
B.1∶9 C.1∶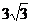 D.1∶
D.1∶
8、在ΔABC中,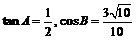 ,若ΔABC的最长边为
,若ΔABC的最长边为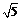 ,则最短边的长为
,则最短边的长为
A.2 B.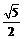 C.
C.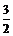 D.1
D.1
9、{an}为等差数列,若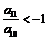 ,且它的前n项和Sn有最小值,那么当Sn取得最小正值时,n=
,且它的前n项和Sn有最小值,那么当Sn取得最小正值时,n=
A.11 B.17 C.19 D.21
10、设对任意实数x∈[−1, 1],不等式x2+ax−3a<0总成立,则实数a的取值范围是
A.a>0 B.a>0或a<−12 C.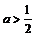 D.
D.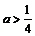
11、已知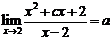 ,且函数
,且函数 在
在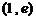 上具有单调性,则
上具有单调性,则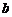 的取值范围是
的取值范围是
A、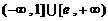 B、
B、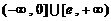 C、
C、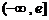 D、
D、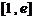
12、如果直线y=kx+1与圆x2+y2+kx+my-4=0交于M、N两点,且M、N关于直线x-y=0对称,动点P(a,b)在不等式组:表示的平面区域内部及边界上运动,则ω=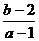 的取值范围是
(
)
的取值范围是
(
)
A、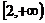 B、
B、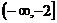 C、
C、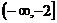 ∪
∪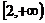 D、
D、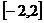
第Ⅱ卷(非选择题 共90分)
在横线上.)
13、将一张画有直角坐标系的图纸折叠一次,使得点A(0,2)与点
B(4,0)重合.若此时点C(7,3)与点D(m,n)重合,则m+n的值
是 .
14、如图,是一个无盖正方体盒子的表面展开图,A,B,C为其上
的三个点,则在正方体盒子中,∠ABC等于 .
15、若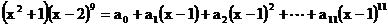 ,
,
则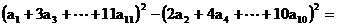 ______(用数字作答).
______(用数字作答).
16、有下列命题:
① G=(G≠0)是a,G,b成等比数列的充分非必要条件;
② 若角α,β满足cosαcosβ=1,则sin(α+β)=0;
③ 若不等式|x-4|+|x-3|<a的解集非空,则必有a≥1;
④ 函数y=sinx+sin|x|的值域是[-2,2].
其中正确命题的序号是 .(把你认为正确的命题的序号都填上)
17、(本小题满分12分)
某次有奖竞猜活动中,主持人准备了A、B两个相互独立的问题, 并且宣布:观众答
对问题A可获奖金a元,答对问题B可获奖金2a元;先答哪个题由观众自由选择;只有第1个问题答对,才能再答第2个问题,否则中止答题。若你被选为幸运观众,且假设你答对问题A、B的概率分别为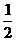 、
、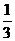 。你觉得应先回答哪个问题才能使你获得奖金的期望较大?说明理由。
。你觉得应先回答哪个问题才能使你获得奖金的期望较大?说明理由。
18、(本小题满分12分)
若函数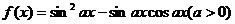 的图象与直线
的图象与直线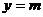 (m为常数)相切,并且切点的横坐标依次成公差为
(m为常数)相切,并且切点的横坐标依次成公差为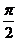 的等差数列.
的等差数列.
(Ⅰ)求m的值;
(Ⅱ)若点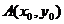 是
是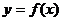 图象的对称中心,且
图象的对称中心,且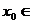 [0,
[0,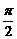 ],求点A的坐标.
],求点A的坐标.
19、(本题满分12分)
如图,O是半径为l的球心,点A、B、C在球面上,OA、OB、OC两两垂直,E、F分别是大圆弧AB与AC的中点,
⑴ 求点E、F在该球面上的球面距离;
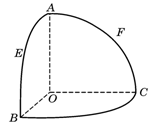 ⑵ 求平面OEF与平面OBC所成的锐二面角。(用反三角函数表示)
⑵ 求平面OEF与平面OBC所成的锐二面角。(用反三角函数表示)
20、(本题满分12分)
已知数列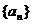 的前
的前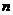 项和为
项和为 ,对一切正整数
,对一切正整数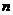 ,点
,点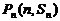 都在函数
都在函数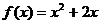 的图象上,且过点
的图象上,且过点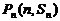 的切线的斜率为
的切线的斜率为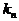 .
.
(Ⅰ)求数列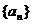 的通项公式;
的通项公式;
(Ⅱ)若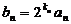 ,求数列
,求数列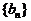 的前
的前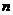 项和为
项和为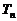 ;
;
(Ⅲ)设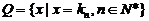 ,
, ,等差数列
,等差数列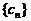 的任一项
的任一项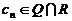 ,其中
,其中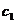 是
是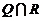 中的最小数,
中的最小数,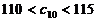 ,求
,求 的通项公式.
的通项公式.
21、 (本题满分12分)
如图,设抛物线C:x2=4y的焦点为F,P(x0, y0)为抛物线上的任一点(其中x0≠0),过P点的切线交y轴于Q点.
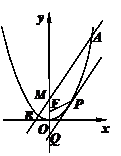 (1)证明:
(1)证明: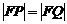 ;
;
(2)Q点关于原点O的对称点为M,过M点作平行于PQ的直线
交抛物线C于A、B两点,若 ,求
,求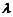 的值.
的值.
22、(本小题满分14分)已知函数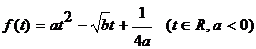 的最大值为正
的最大值为正
实数,集合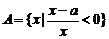 ,集合
,集合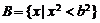 。
。
(1)求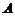 和
和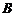 ;
;
(2)定义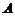 与
与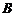 的差集:
的差集: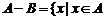 且
且 。
。
设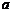 ,
,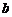 ,
,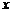 均为整数,且
均为整数,且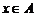 。
。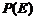 为
为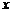 取自
取自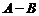 的概率,
的概率,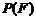 为
为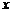 取自
取自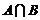 的概率,写出
的概率,写出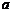 与
与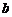 的二组值,使
的二组值,使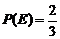 ,
,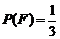 。
。
(3)若函数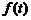 中,
中,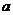 ,
,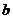 是(2)中
是(2)中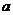 较大的一组,试写出
较大的一组,试写出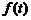 在区间[
在区间[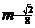 ,
,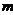 ]上的最大值函数
]上的最大值函数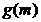 的表达式。
的表达式。
高考理科数学仿真测试卷 理科数学(二) 本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分。考试时间120分钟。 参考公式: 如果事件A、B互诉,那么: 如果事件A、B相互独立,那么 如果事件A在一次试验中发生的概率是P,那行n次独立重复试验中恰好发生k次的概率是: 球的表面积公式:其中R表示球的半径. 球的体积公式:,其中R表示球的半径. 区域作答。 3.考试结束,监考人员将第Ⅰ卷和第Ⅱ卷一并收回。 第Ⅰ卷(选择题 共60分)参考答案
参考答案:
一、选择题:
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
答案 |
A |
B |
C |
D |
D |
B |
D |
D |
C |
C |
A |
C |
简答与提示:
1、集合M是函数y=x+l的函数值的集合,集合N是圆上的点集.
2、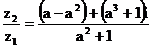 ,故a 3+1=0,得a =-1.
,故a 3+1=0,得a =-1.
3、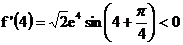 .
.
4、若使夹角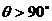 ,则有-m+n<0即m>n,其概率为
,则有-m+n<0即m>n,其概率为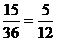 .
.
5、按定义计算
6、由已知f (3x+1)=f[3(x+3)+1]=f(3x+1+9),所以f(x)的周期为9,f(2006)=f(2007-1)=f(-1)=
-f(1)=1.
7、面积比是相似比的平方,体积比是相似比的立方
8、由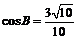 得
得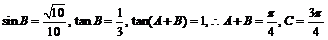 ,
,
∴∠C的对边AB为最长边,∠B的对边AC为最短边,由正弦定理得:
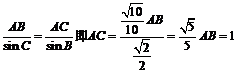
9、∵Sn有最小值,∴d<0则a10>a11,又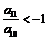 ,∴a11<0<a10 ∴a10+a11<0,
,∴a11<0<a10 ∴a10+a11<0,
S20=10(a1+a20)=10(a10+a11)<0, S19=19a10>0又a1>a2>…>a10>0>a11>a12>…
∴S10>S9>…>S2>S1>0, S10>S11>…>S19>0>S20>S21>…
又∵S19−S1=a2+a3+…+a19=9(a10+a11)<0 ∴S19为最小正值
10、由不等式x2+ax−3a<0, x∈[−1, 1]时恒成立,可得不等式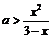 ,x∈[−1,
1]时恒成立,令
,x∈[−1,
1]时恒成立,令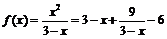 ,由x∈[−1,
1]得3−x∈[2, 4],当3−x=3即x=0时,函数f(x)有最小值0,又
,由x∈[−1,
1]得3−x∈[2, 4],当3−x=3即x=0时,函数f(x)有最小值0,又
11、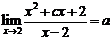
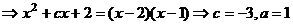 ,
,
∴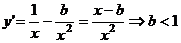 或
或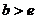
12、 M、N关于直线x-y=0对称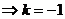 且圆心
且圆心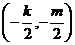 在直线x-y=0上,从而
在直线x-y=0上,从而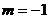
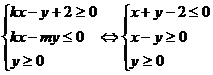 ;ω=
;ω=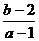 看成斜率。
看成斜率。
二、填空题:
13、 14、60o 15、0 16、①②③④
简答与提示:
13、直线对称
14、将正方体复原
15、0 两边求导,再分别把x赋值x=2,x=0,最后把所得两式相乘即得.
16、①注意到G≠0; ②cosαcosβ=1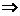 cosα=cosβ=1或cosα=cosβ=-1;
cosα=cosβ=1或cosα=cosβ=-1;
③ 记f(x)=|x-4|+|x-3|<a,依题意则有a≥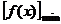 1;
1;
④ y=sinx+sin|x| 。
。
三、解答题:
17、(本小题满分12分)
解:设甲先答A、B所获奖金分别为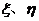 元,则有
元,则有
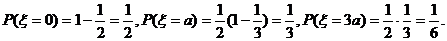 …… 3分
…… 3分
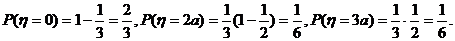 ……6分
……6分
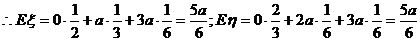 …………10分
…………10分
由于两种答序获奖金的期望相等,故先答哪个都一样。 …………………………12分
18、(本小题满分12分)
解:(Ⅰ)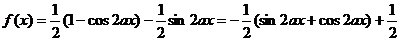
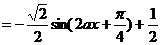 …………………………………4分
…………………………………4分
∵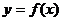 的图象与
的图象与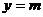 相切.
相切.
∴m为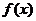 的最大值或最小值.
即
的最大值或最小值.
即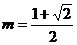 或
或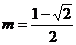 ……6分
……6分
(Ⅱ)又因为切点的横坐标依次成公差为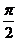 的等差数列.所以
的等差数列.所以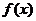 最小正周期为
最小正周期为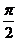 .
.
又
 所以
所以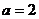 ……………………………8分
……………………………8分
即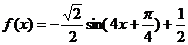 ……………………………………9分
……………………………………9分
令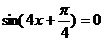 .则
.则
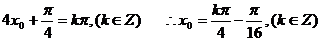 ………………………10分
………………………10分
由0≤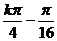 ≤
≤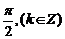 得k=1,2,
得k=1,2,
因此对称中心为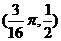 、
、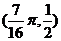 . ……………………………12分
. ……………………………12分
19、(本题满分12分)
解:⑴解法一:如图1,证明0M=0N=MN=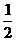 AB=
AB=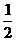 BC=
BC=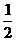 AC,从而∠MON=
AC,从而∠MON=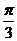
∴点E、F在该球面上的球面距离为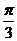 .
.
解法二:如图2,补形易证:∠EOF=∠GOH =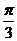 .
.
解法三:其实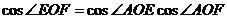 ,易证:∠EOF=
,易证:∠EOF=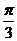 .
.
解法四:如图3,建立空间直角坐标系,易知E(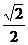 ,0,
,0, 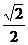 )、F(0,
)、F(0,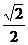 ,
, 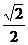 )
)
∴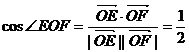 ,从而∠EOF =
,从而∠EOF =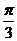 . …………………6分
. …………………6分
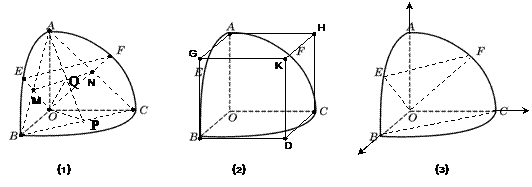 |
⑵ 解法一:如图1,取BC中点P,连接AP交MN与Q,则易证,∠POQ就是所求二面角的平面角。
在三角形OPQ中,OP=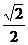 ,PQ=OQ=
,PQ=OQ=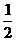 AP=
AP=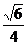 ,可解得cos∠POQ=
,可解得cos∠POQ=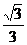 ,
,
∴∠POQ=arcos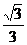 (=arctan
(=arctan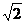 ).
……………………………12分
).
……………………………12分
解法二:如图2,补形成正方体去解决.
解法三:如图3,建立空间直角坐标系去求解。
20、(本题满分12分)
解:(Ⅰ)因为点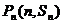 都在函数
都在函数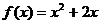 的图象上
的图象上
所以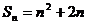
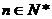
当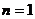 时,
时,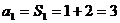 ……………………………………………2分
……………………………………………2分
当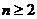 时,
时,
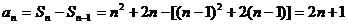 (*) ……………3分
(*) ……………3分
令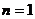 ,
,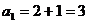 ,也满足(*)式
,也满足(*)式
所以,数列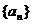 的通项公式是
的通项公式是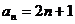 . …………………………………4分
. …………………………………4分
(Ⅱ)由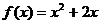 求导可得
求导可得
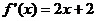
∵ 过点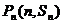 的切线的斜率为
的切线的斜率为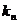
∴ 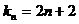 …………………………………………………………5分
…………………………………………………………5分
又∵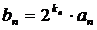
∴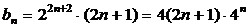 ……………………………6分
……………………………6分
∴ 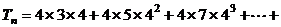
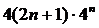 ① 由①
① 由①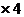 可得
可得
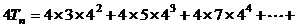
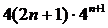 ②
②
①-②可得
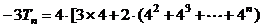
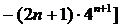
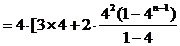
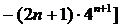
∴ 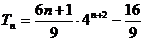 ……………………………………………………8分
……………………………………………………8分
(Ⅲ)∵ ,
,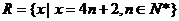
∴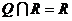 --------------------------- 10分
--------------------------- 10分
又∵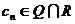 ,其中
,其中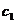 是
是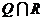 中的最小数,
中的最小数,
∴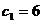 , --------------------------- 11分
, --------------------------- 11分
∴ 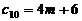
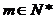 (
(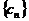 的公差是4 的倍数!)
的公差是4 的倍数!)
又∵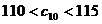
∴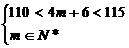 解得
解得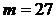
∴ ………………………………………………………………………10分
………………………………………………………………………10分
设等差数列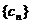 的公差为
的公差为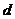
则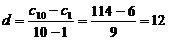
∴ 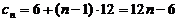
所以,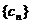 的通项公式为
的通项公式为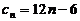 . ……………………………12分
. ……………………………12分
21、(本题满分12分)
(1)证明:由抛物线定义知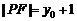 ,(2分)
,(2分)
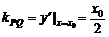 ,可得PQ所在直线方程为x0x=2(y+y0), ………………………4分
,可得PQ所在直线方程为x0x=2(y+y0), ………………………4分
得Q点坐标为(0, -y0),∴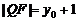 ,∴ |PF|=|QF|,∴△PFQ为等腰三角形。 …6分
,∴ |PF|=|QF|,∴△PFQ为等腰三角形。 …6分
(2)设A(x1, y1),B(x2, y2),又M点坐标为(0, y0), ∴AB方程为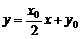 ,
,
由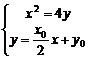 得
得
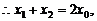
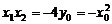 ……①
……①
由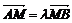 得:
得: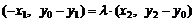 , ∴
, ∴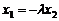 ……②
……②
由①②知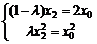 ,得
,得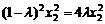 ,由x0≠0可得x2≠0,
,由x0≠0可得x2≠0,
∴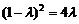 ,又
,又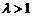 ,解得:
,解得: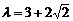 . ………………………………12分
. ………………………………12分
22、(本小题满分14分)
(1)∵ ,配方得
,配方得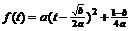 ,
,
由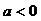 得最大值
得最大值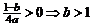 。……………………………………………3分
。……………………………………………3分
∴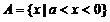 ,
,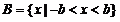 。
…………………………5分
。
…………………………5分
(2)要使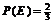 ,
,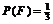 。可以使
。可以使
①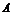 中有3个元素,
中有3个元素,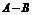 中有2个元素,
中有2个元素,
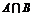 中有1个元素。
中有1个元素。
则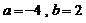 。 …………………………………………………………………8分
。 …………………………………………………………………8分
②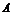 中有6个元素,
中有6个元素,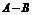 中有4个元素,
中有4个元素,
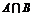 中有2个元素。
中有2个元素。
则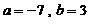 ……………………………………………………………………10分
……………………………………………………………………10分
(3)由(2)知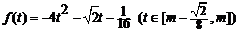 …………………………11分
…………………………11分
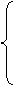
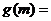
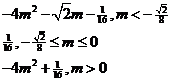 ……………………………………………14分
……………………………………………14分