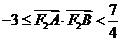1. 设全集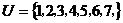 ,
,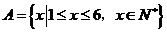 ,则
,则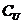 A=( )
A=( )
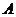 .
.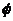
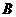 .
. 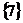
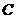 .
.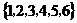
 .
.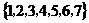
2. 若复数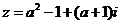 是纯虚数(其中
是纯虚数(其中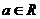 ),则
),则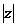 = ( )
= ( )
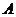 .0
.0
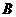 .
.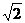
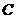 .2
.2  .4
.4
3.某中学高一年级有学生600人,高二年级有学生450人,高三年级有学生750人,现用分层抽样的方法从中抽取一个容量为360的样本进行某项调查,则应抽取的高二年级的学生数为( )
 .90
.90  .120
.120 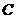 .240
.240
 .360
.360
4. 已知等差数列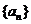 的前
的前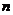 项的和为
项的和为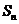 ,且
,且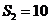 ,
,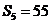 ,则和过点
,则和过点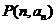 和点
和点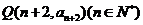 的直线平行的一个向量的坐标是( )
的直线平行的一个向量的坐标是( )
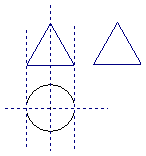 A.
A.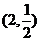 B.
B. C.
C.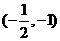 D.
D.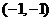
5. 如图,一个空间几何体的主视图和左视图都是边长为1的正三角形,
俯视图是一个圆,那么这个几何体的侧面积为( )
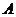 .
. 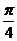
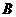 .
. 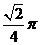
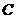 .
. 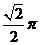
 .
. 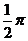
6. 已知命题P: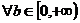 ,
,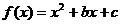 在
在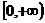 上为增函数;命题Q:
上为增函数;命题Q: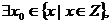 使
使 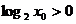 ,则下列结论成立的是 ( )
,则下列结论成立的是 ( )
 .﹁P∨﹁Q
.﹁P∨﹁Q  .﹁P∧﹁Q
.﹁P∧﹁Q  .P∨﹁Q
.P∨﹁Q  .P∧﹁Q
.P∧﹁Q
7. 设函数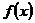
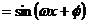
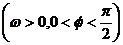 .若将
.若将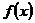 的图象沿x轴向右平移
的图象沿x轴向右平移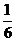 个单位长度,得到的图象经过坐标原点;若将
个单位长度,得到的图象经过坐标原点;若将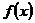 的图象上所有的点的横坐标缩短到原来的
的图象上所有的点的横坐标缩短到原来的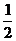 倍(纵坐标不变), 得到的图象经过点
倍(纵坐标不变), 得到的图象经过点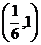 . 则 ( )
. 则 ( )
A.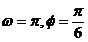 B.
B.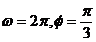 C.
C. 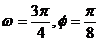 D. 适合条件的
D. 适合条件的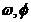 不存在
不存在
8. 已知非负实数x、y同时满足2x+y-4≤0,x+y-1≥0,则z=x2+(y+2)2的最小值是 ( )
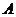 .
.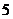
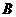 .
.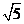
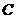 .
. 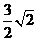
 .
.
9. 设f(x) = 3x-x2,则在下列区间中,使函数f(x)有零点的区间是 ( )
A.[0,1] B.[1,2] C.[-2,-1] D.[-1,0]
10. 已知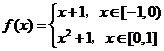 ,则下列函数的图象错误的是 ( )
,则下列函数的图象错误的是 ( )
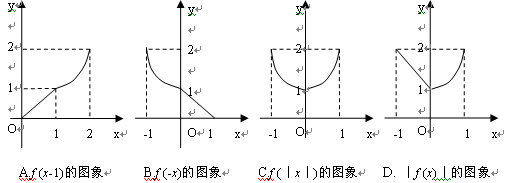
必做题:
11.圆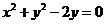 的圆心到直线
的圆心到直线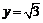 x的距离是__________________.
x的距离是__________________.
12.如图是计算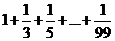 的程序框图,判断框应填的内容是____,处理框应填的内容是____.
的程序框图,判断框应填的内容是____,处理框应填的内容是____.
13. 已知
已知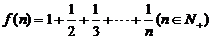 , 经计算得
, 经计算得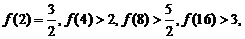
 ,推测当
,推测当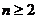 时,有_____________________.
时,有_____________________.
选做题:
14.将极坐标方程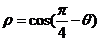 化为直角坐标方程是____________.
化为直角坐标方程是____________.
15.如图,四边形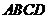 是等腰梯形,
是等腰梯形,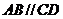 .由4个
.由4个
这样的等腰梯形可以拼出图乙所示的平行四边形,则四边形
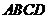 中
中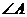 度数为
.
度数为
.


16.(本小题满分12分)在ΔABC中,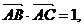
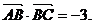
⑴求AB边的长度; ⑵求 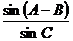 的值.
的值.
17. (本题满分12分) 已知等差数列{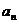 }中
}中 =
=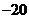 ,
,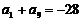 ,
,
(Ⅰ)求数列{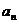 }的通项公式;
}的通项公式;
(Ⅱ)若数列{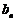 }满足
}满足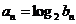 ,设
,设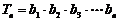 且
且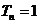 ,求
,求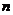 的值.
的值.
18.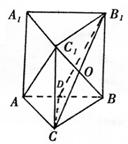 (本题满分14分) 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC = 3,BC = 4,AB = 5,AA1=4,点D是AB的中点.
(本题满分14分) 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC = 3,BC = 4,AB = 5,AA1=4,点D是AB的中点.
(1)求证:AC⊥BC1;
(2)求证:AC1∥平面CDB1;
(3)求异面直线AC1与B1C所成角的余弦值.
19.(本题满分14分) 某地政府招商引资,为吸引外商,决定第一年产品免税,某外资厂该年A型产品出厂价为每件60元,年销售量为11.8万件.第二年,当地政府开始对该商品征收税率为p%
(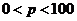 ,即销售100元要征收p元) 的税收,于是该产品的出厂价上升为每件
,即销售100元要征收p元) 的税收,于是该产品的出厂价上升为每件 元,预计年销售量将减少p万件.
元,预计年销售量将减少p万件.
(Ⅰ) 将第二年政府对该商品征收的税收y(万元)表示成p的函数,并指出这个函数的定义域;
(Ⅱ) 要使第二年该厂的税收不少于16万元,则税率p%的范围是多少?
(Ⅲ) 在第二年该厂的税收不少于16万元的前提下,要让厂家获得最大销售金额,则p应为多少?
20. (本题满分14分) 在实数集R上定义运算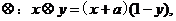 若
若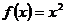 ,
,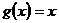 ,若
,若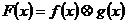 .
.
(Ⅰ) 求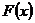 的解析式; (Ⅱ) 若
的解析式; (Ⅱ) 若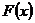 单在
单在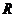 上是减函数,求实数
上是减函数,求实数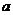 的取值范围;
的取值范围;
(Ⅲ) 若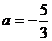 ,
,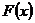 的曲线上是否存在两点,使得过这两点的切线互相垂直,若存在,求出切线方程;若不存在,说明理由.
的曲线上是否存在两点,使得过这两点的切线互相垂直,若存在,求出切线方程;若不存在,说明理由.
21. (本题满分14分)设椭圆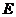 :
: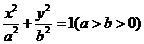 的左、右焦点分别为
的左、右焦点分别为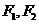 ,已知椭圆
,已知椭圆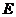 上的任意一点
上的任意一点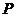 ,满足
,满足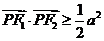 ,过
,过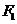 作垂直于椭圆长轴的弦长为3.
作垂直于椭圆长轴的弦长为3.
(1)求椭圆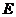 的方程;
的方程;
(2)若过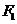 的直线交椭圆于
的直线交椭圆于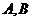 两点,求
两点,求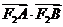 的取值范围.
的取值范围.
高考文科数学模拟试题(文科4)参考答案
数学试题(文科4)参考答案
一、选择题 B C A B D C A A D D
二、填空题
|
题号 |
11 |
12 |
13 |
14 |
15 |
|
答案 |
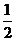 |
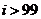 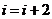 |
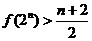 |
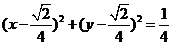 |
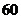 |
三、解答题
16.解:(1)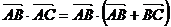
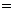
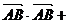
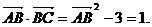
∴ 即AB边的长度为2.
…………… …………5分
即AB边的长度为2.
…………… …………5分
(2)由已知及(1)有: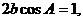
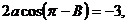
∴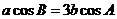 ……………8分
……………8分
由正弦定理得: 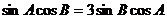 ……………10分
……………10分
∴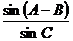 =
=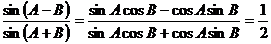 …………12分
…………12分
17. (Ⅰ) 解: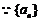 为等差数列
为等差数列
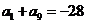
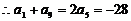 ,…………………2分
,…………………2分
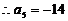 又
又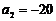 设{
设{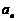 }的公差为d,
}的公差为d,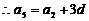 ,∴d=2, …………4分
,∴d=2, …………4分
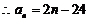 ……………………………………………6分
……………………………………………6分
(Ⅱ) 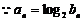 ……………………………………………………………8分
……………………………………………………………8分
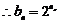
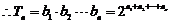
当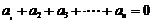 时,
时,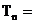
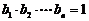 ……………………………10分
……………………………10分
即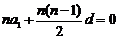 ,
,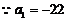
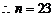 即n=23时,
即n=23时, 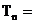 1 ……………12分
1 ……………12分
18.解:(1)∵AC2 + BC2 = AB2 ∴AC⊥BC 又∵CC1∥AA1,AA1⊥面ABC
∴CC1⊥面ABC ∴AC⊥C1C ∴AC⊥面BCC1B1,
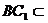 平面BCC1B1
∴AC⊥BC1, ……………………………………4分
平面BCC1B1
∴AC⊥BC1, ……………………………………4分
(2)设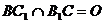 ,则O为BC1中点,连OD,
,则O为BC1中点,连OD,
∵D为AB中点 ∴OD∥AC1,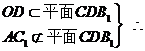 AC1∥平面CDB1;……8分
AC1∥平面CDB1;……8分
(3)由(2)知,OD∥AC1 ∴OD与B1C所成的角即为AC1与B1C所成角,∴∠DOC为所求
在△ODC中,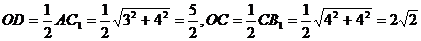
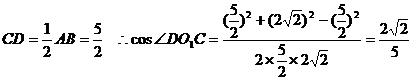 …………14分
…………14分
19. (Ⅰ) 解:依题意,第二年该商品年销售量为(11.8-p)万件,
年销售收入为 (11.8一
(11.8一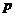 )万元,……………………………………………2
)万元,……………………………………………2
政府对该商品征收的税收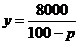 (11.8一p)p%(万元)
(11.8一p)p%(万元)
故所求函数为 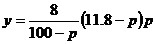 ……………………………………………4
……………………………………………4
由11.8-p>0及p>0得定义域为0<p<11.8 ……………………………………6分
(Ⅱ) 解: 由y≥16得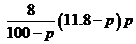 ≥16
≥16
化简得p2-12p+20≤0,即(p-2)(p-10)≤0,解得2≤p≤l0
故当税率为[2%,10%]内时,税收不少于16万元.…………………………………10分
(Ⅲ) 解:第二年,当税收不少于16万元时,
厂家的销售收入为g(p)= 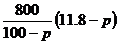 (2≤p≤10)
(2≤p≤10)
∵ g(p)=
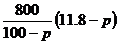 =600(10+
=600(10+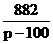 )在
)在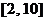 是减函数, …………………
是减函数, …………………
∴ g(p)max =g(2)=600(万元)
故当比率为2%时,厂家销售金额最大。 ……………………………14分
20.解:(Ⅰ)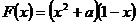 =
=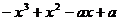 …………………………3分
…………………………3分
(Ⅱ)∵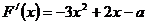 …………………………………4分
…………………………………4分
当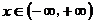 上时,
上时,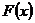 单调递减
单调递减
∴ 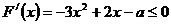 ,
,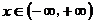 恒成立 ………………………6分
恒成立 ………………………6分
∴△=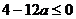 解得:
解得: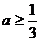 ……………………………7分
……………………………7分
(Ⅲ)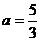 时,
时,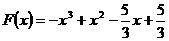 ………………………………8分
………………………………8分
设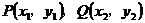 是
是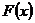 曲线上的任意两点
曲线上的任意两点
∵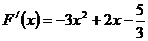
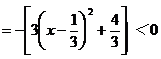 ……………………………10分
……………………………10分
∴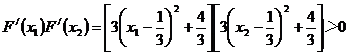 ……………………12分
……………………12分
∴ 不成立…………………………13分
不成立…………………………13分
∴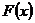 的曲线上不存在两点,使得过这两点的切线互相垂直。……………………14分
的曲线上不存在两点,使得过这两点的切线互相垂直。……………………14分
21. 解:(1)设点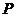
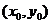 ,则
,则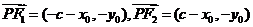 ,
,
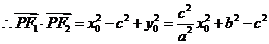 ,
,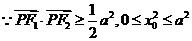
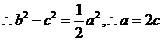 ,又
,又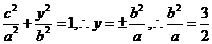 ,
,
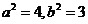 ,∴椭圆的方程为:
,∴椭圆的方程为: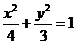
(2)当过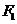 直线
直线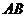 的斜率不存在时,点
的斜率不存在时,点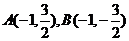 ,则
,则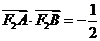 ;
;
当过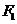 直线
直线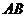 的斜率存在时,设斜率为
的斜率存在时,设斜率为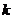 ,则直线
,则直线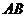 的方程为
的方程为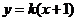 ,
,
设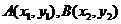 , 由
, 由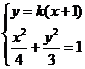 得:
得: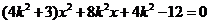
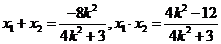
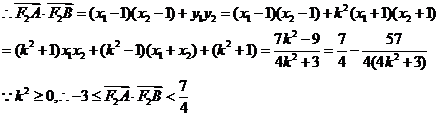
综合以上情形,得: