
1. 若集合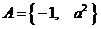 ,
, ,则“
,则“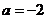 ”是“
”是“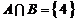 ”的 (
A )
”的 (
A )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
2. 已知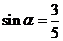 ,
,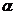 为钝角,则
为钝角,则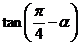 的值为
( B )
的值为
( B )
A.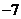 B.
B.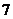 C.
C.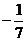 D.
D.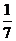
3. 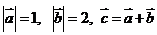 ,且
,且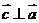 ,则向量
,则向量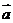 与
与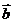 的夹角为
( C )
的夹角为
( C )
A.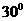 B.
B.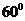 C.
C.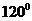 D.
D.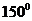
4. 设变量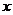 ,
,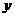 满足约束条件
满足约束条件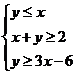 ,则目标函数
,则目标函数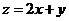 的最小值为 (
B )
的最小值为 (
B )
A.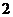 B.
B.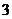 C.
C.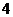 D.
D.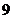
5.对于直线m、n和平面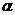 ,下面命题中的真命题是 (
C )
,下面命题中的真命题是 (
C )
A.如果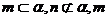 、n是异面直线,那么
、n是异面直线,那么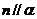
B.如果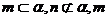 、n是异面直线,那么
、n是异面直线,那么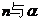 相交
相交
C.如果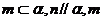 、n共面,那么
、n共面,那么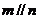
D.如果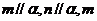 、n共面,那么
、n共面,那么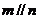
6. 为了得到函数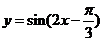 的图像,可以将y=sin2x的图像 (
A )
的图像,可以将y=sin2x的图像 (
A )
A.向右平移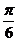 个单位 B.向左平移
个单位 B.向左平移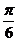 个单位 C.向右平移
个单位 C.向右平移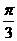 个单位 D.向左平移
个单位 D.向左平移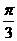 个单位
个单位
7. 若椭圆的对称轴为坐标轴,长轴长与短轴长的和为 ,焦距为
,焦距为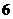 ,则椭圆的方程为(
C )
,则椭圆的方程为(
C )
A.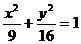 B.
B.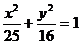 C.
C.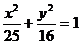 或
或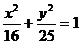 D.以上都不对
D.以上都不对
8. 已知△ABC的周长为9,且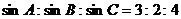 ,则cosC的值为 ( A )
,则cosC的值为 ( A )
A.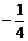 B.
B.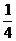 C.
C.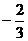 D.
D.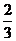
9.设函数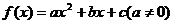 ,对任意实数t都有
,对任意实数t都有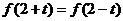 成立,则函数值
成立,则函数值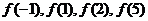 中,最小的一个不可能是 (
B )
中,最小的一个不可能是 (
B )
A.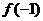 B.
B.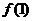 C.
C.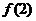 D.
D.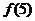
|
8 |
3 |
4 |
|
1 |
5 |
9 |
|
6 |
7 |
2 |
10. 将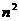 个正整数
个正整数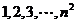 填入
填入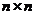 方格中,使其每行、每列、每条对角线上的数的和都相等,这个正方形叫做
方格中,使其每行、每列、每条对角线上的数的和都相等,这个正方形叫做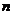 阶幻方.记
阶幻方.记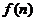 为
为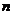 阶幻方对角线上数的和,如右图就是一个
阶幻方对角线上数的和,如右图就是一个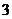 阶幻方,可知
阶幻方,可知 .已知将等差数列:
.已知将等差数列: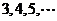 前
前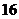 项填入
项填入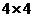 方格中,可得到一个
方格中,可得到一个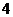 阶幻方,则其对角线上数的和等于 ( C )
阶幻方,则其对角线上数的和等于 ( C )
A.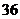 B.
B.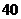 C.
C.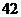 D.
D.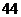
必做题: 以下三题为必做题.
11. 程序框图(如图)的运算结果为 。
12.某校高一新生有480名学生,初一新生有420名学生,
现要用分层抽样的方法从中抽取一个容量为150的的样本,
则需要从高一新生中抽取的学生人数为 .
13.数列1,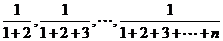 的前
的前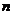 项和为
。
项和为
。
选做题: 从以下两题中选做一题,如两题都做,按第一题的得分记分.
14.自极点O向直线l作垂线,垂足是H(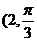 ),则直线l的极坐标方程为 。
),则直线l的极坐标方程为 。
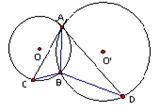
15. 如图,⊙O和⊙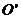 都经过A、B两点,AC是⊙
都经过A、B两点,AC是⊙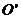
的切线,交⊙O于点C,AD是⊙O的切线,交⊙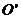 于
于
点D,若BC= 2,BD=6,则AB的长为 。
16.(本小题满分12分)
已知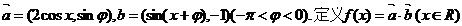 ,且
,且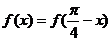 对任意实数x恒成立.
对任意实数x恒成立.
(Ⅰ)求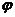 的值;
的值;
|
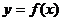 的单调增区间.
的单调增区间.
17.(本题满分12分)
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,点E是PD的中点.
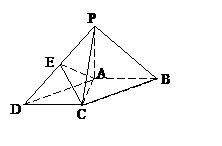 (1)求证:AC⊥PB;(2)求证:PB//平面AEC.
(1)求证:AC⊥PB;(2)求证:PB//平面AEC.
18.(本小题满分14分)
某种人群中各种血型的人所占的比如下表所示:
|
血型 |
A |
B |
AB |
O |
|
该血型的人所占比% |
28 |
29 |
8 |
35 |
已知同种血型的人可以输血,O型血可以输给任一种血型的人,任何人的血都可以输给AB型血的人,其他不同血型的人不能互相输血。小明是B型血,若小明因病需要输血,问:(1)任找一人,其血可以输给小明的概率是多少?
(2)任找一人,其血不能输给小明的概率是多少?
19.(本小题满分14分)
某种细胞开始时有2个,1小时后分裂为4个并死去1个,2小时后分裂为6个并死去1个,3小时后分裂为10个并死去1个,…,按照这种规律进行下去。设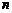 小时后细胞的个数为
小时后细胞的个数为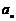 个
个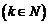 。
。
(Ⅰ)求数列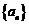 的通项公式;
的通项公式;
(Ⅱ)求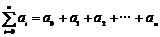 的表达式。
的表达式。
20.(本小题满分14分)
设函数f(x)=x3+ax2+bx+c在x=1处取得极值-2,试用c表示a和b,并求f(x)的单调区间。
21.(本小题满分14分)
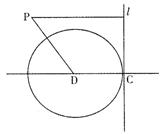 如图,已知直线l与半径为1的⊙D相切于点C,动点P到直线l的距离为d,若
如图,已知直线l与半径为1的⊙D相切于点C,动点P到直线l的距离为d,若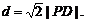
(Ⅰ)求点P的轨迹方程;
(Ⅱ)若轨迹上的点P与同一平面上的点G、M分别满足
 ,
,
求以P、G、D为项点的三角形的面积.
高考文科数学模拟试题 ( 文 科 2 )参考答案
数 学 试 题 ( 文 科 2 )参考答案
一.选择题: A B C B C A C A B C
二.填空题: 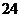 ; 80;
; 80;
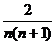 ;
; 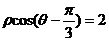 ;
; 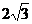 。
。
三.解答题。
16.解:(Ⅰ)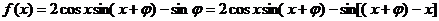
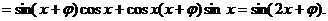 ……………2分
……………2分
由题意知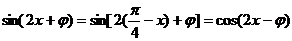 对任意实数x恒成立,
对任意实数x恒成立,
得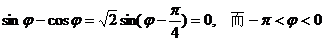 ,
,
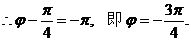 ………………………………………………………6分
………………………………………………………6分
(Ⅱ)由(Ⅰ)知
由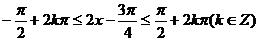 ,解得
,解得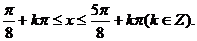
所以,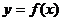 的单调增区间为
的单调增区间为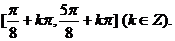 ……………………12分
……………………12分
17.证明:(1) ∵PA⊥平面ABCD,则PA⊥AC,由AB⊥AC,∴AC⊥平面PAB,∴AC⊥PB.
(2)连接BD交AC于F,因四边形ABCD是平行四边形,则F是BD中点,又∵E是PD中点,则EF是△PDB是中位线,∴EF//PB,又∵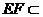 平面EAC,∴PB//平面AEC.
平面EAC,∴PB//平面AEC.
18.解:对任一人,其血型为A,B,AB,O型血的事件分别记为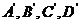 ,它们是互斥的。由已知有:
,它们是互斥的。由已知有:
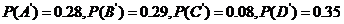 ,因为B,O型血可以输给B型血的人,故“可以输给B型血的人”为事件
,因为B,O型血可以输给B型血的人,故“可以输给B型血的人”为事件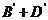 ,有:
,有: 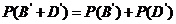 =0.29+0.35=0.64
=0.29+0.35=0.64
(2)由于A,AB型血不能输给B型血的人,故“不能输给B型血的人”为事件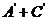 ,
,
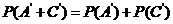 =0.28+0.08=0.36
=0.28+0.08=0.36
答:任找一人,其血可以输给小明的概率是0.64,任找一人,其血不能输给小明的概率是0.36
19.解:(Ⅰ)由题意可知,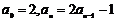 ,即
,即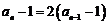 ………(9分)
………(9分)
∴数列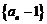 构成以
构成以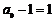 为首项,以2为公比的等比数列,
为首项,以2为公比的等比数列,
∴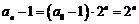 ,∴
,∴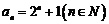 …………………………(9分)
…………………………(9分)
(Ⅱ)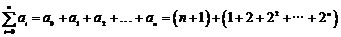
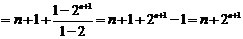 ……………………………(14分)
……………………………(14分)
20.解:依题意有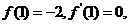 而
而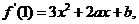

故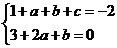 得
得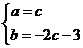 从而
从而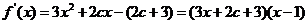 。
。
令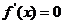 ,得
,得 或
或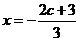 。
。
由于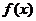 在
在 处取得极值,故
处取得极值,故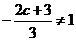 ,即
,即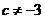 。
。
(1) 若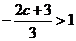 ,即
,即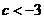 ,则当
,则当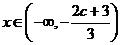 时,
时,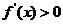 ;
;
当 时,
时,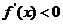 ;当
;当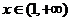 时,
时,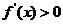 ;
;
从而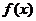 的单调增区间为
的单调增区间为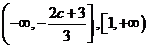 ;单调减区间为
;单调减区间为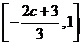
(2) 若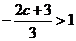 ,即
,即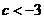 ,同上可得,
,同上可得,
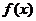 的单调增区间为
的单调增区间为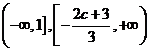 ;单调减区间为
;单调减区间为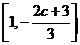
21.解:(Ⅰ)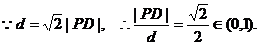
∴点P的轨迹是D为焦点,l为相应准线的椭圆.
由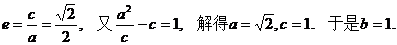
以CD所在直线为x轴,以CD与⊙D的另一个交点O为坐标原点建立直角坐标系.
∴所求点P的轨迹方程为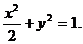 ………………………………………………6分
………………………………………………6分
(说明:其它建系方式相应给分)
(Ⅱ)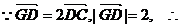 G为椭圆的左焦点.
G为椭圆的左焦点.
又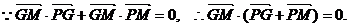
由题意,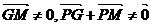 (否则P、G、M、D四点共线与已经矛盾)
(否则P、G、M、D四点共线与已经矛盾)
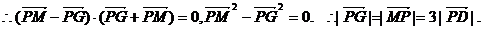
又∵点P在椭圆上, 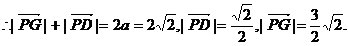
又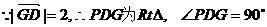
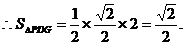 ……………………………………………………14分
……………………………………………………14分