
1.下列函数中,反函数是其自身的函数为( )
A.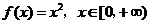 B.
B.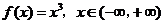
C.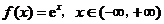 D.
D.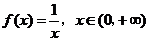
2.设 均为直线,其中
均为直线,其中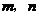 在平面
在平面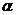 内,则“
内,则“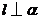 ”是“
”是“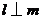 且
且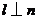 ”的(
)
”的(
)
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.若对任意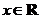 ,不等式
,不等式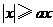 恒成立,则实数
恒成立,则实数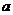 的取值范围是(
)
的取值范围是(
)
A.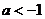 B.
B.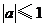 C.
C.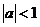 D.
D.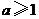
4.若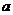 为实数,
为实数,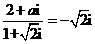 ,则
,则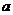 等于(
)
等于(
)
A.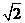 B.
B.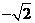 C.
C.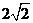 D.
D.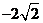
5.若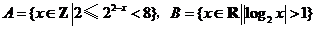 ,则
,则 的元素个数为(
)
的元素个数为(
)
A.0 B.1 C.2 D.3
6.函数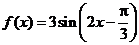 的图象为
的图象为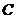 ,
,
①图象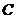 关于直线
关于直线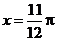 对称;
对称;
②函数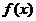 在区间
在区间 内是增函数;
内是增函数;
③由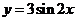 的图象向右平移
的图象向右平移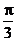 个单位长度可以得到图象
个单位长度可以得到图象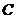 .
.
以上三个论断中,正确论断的个数是( )
A.0 B.1 C.2 D.3
7.如果点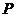 在平面区域
在平面区域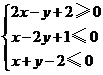 上,点
上,点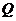 在曲线
在曲线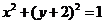 上,那么
上,那么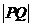 的最小值为(
)
的最小值为(
)
A.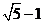 B.
B.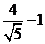 C.
C.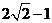 D.
D.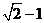
8.半径为1的球面上的四点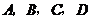 是正四面体的顶点,则
是正四面体的顶点,则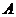 与
与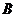 两点间的球面距离为(
)
两点间的球面距离为(
)
 A.
A.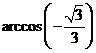 B.
B.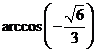 C.
C.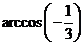 D.
D.
9.如图,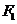 和
和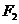 分别是双曲线
分别是双曲线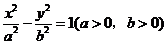
的两个焦点,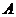 和
和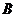 是以
是以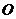 为圆心,以
为圆心,以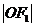 为半径的圆与
为半径的圆与
该双曲线左支的两个交点,且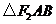 是等边三角形,则双
是等边三角形,则双
曲线的离心率为( )
|
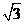 B.
B.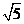
C.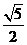 D.
D.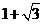
10.以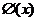 表示标准正态总体在区间
表示标准正态总体在区间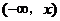 内取值的概率,若随机变量
内取值的概率,若随机变量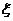 服从正态分布
服从正态分布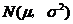 ,则概率
,则概率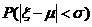 等于(
)
等于(
)
A. B.
B.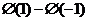
C.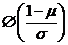 D.
D.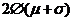
11.定义在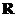 上的函数
上的函数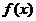 既是奇函数,又是周期函数,
既是奇函数,又是周期函数,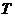 是它的一个正周期.若将方程
是它的一个正周期.若将方程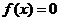 在闭区间
在闭区间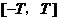 上的根的个数记为
上的根的个数记为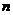 ,则
,则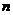 可能为(
)
可能为(
)
A.0 B.1 C.3 D.5
第Ⅱ卷(非选择题 共95分)
12.若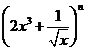 的展开式中含有常数项,则最小的正整数
的展开式中含有常数项,则最小的正整数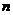 等于
.
等于
.
13. 在四面体
在四面体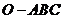 中,
中,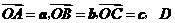 为
为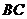 的中点,
的中点,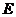 为
为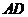 的中点,则
的中点,则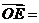 (用
(用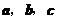 表示).
表示).
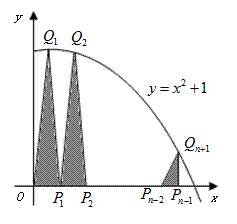
14.如图,抛物线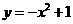 与
与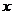 轴的正半轴交于点
轴的正半轴交于点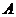 ,
,
将线段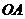 的
的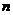 等分点从左至右依次记为
等分点从左至右依次记为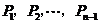 ,
,
过这些分点分别作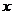 轴的垂线,与抛物线的交点依次为
轴的垂线,与抛物线的交点依次为
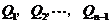 ,从而得到
,从而得到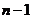 个直角三角形
个直角三角形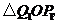
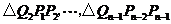 .当
.当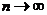 时,这些三角形
时,这些三角形
|
15.在正方体上任意选择4个顶点,它们可能是如下各种几何形体的4个顶点,这些几何形体是 (写出所有正确结论的编号).
①矩形;
②不是矩形的平行四边形;
③有三个面为等腰直角三角形,有一个面为等边三角形的四面体;
④每个面都是等边三角形的四面体;
⑤每个面都是直角三角形的四面体.
16.(本小题满分12分)
已知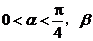 为
为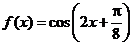 的最小正周期,
的最小正周期,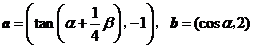 ,且
,且
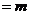 .求
.求 的值.
的值.
17.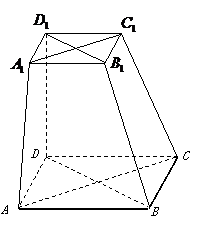 (本小题满分14分)
(本小题满分14分)
如图,在六面体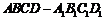 中,四边形
中,四边形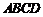 是边长为
是边长为
2的正方形,四边形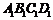 是边长为1的正方形,
是边长为1的正方形,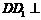 平面
平面
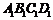 ,
,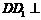 平面
平面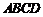 ,
,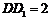 .
.
(Ⅰ)求证: 与
与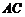 共面,
共面,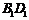 与
与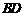 共面.
共面.
(Ⅱ)求证:平面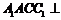 平面
平面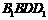 ;
;
(Ⅲ)求二面角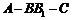 的大小(用反三角函数值表示).
的大小(用反三角函数值表示).
|
18.(本小题满分14分)
设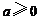 ,
,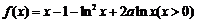 .
.
(Ⅰ)令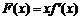 ,讨论
,讨论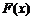 在
在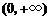 内的单调性并求极值;
内的单调性并求极值;
(Ⅱ)求证:当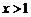 时,恒有
时,恒有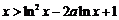 .
.
19.(本小题满分12分)
 如图,曲线
如图,曲线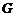 的方程为
的方程为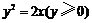 .以原点为圆心.以
.以原点为圆心.以 为半径的圆分别与曲线
为半径的圆分别与曲线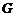 和
和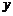 轴的正半轴相交于点
轴的正半轴相交于点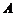 与点
与点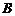 .直线
.直线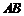 与
与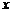 轴相交于点
轴相交于点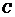 .
.
(Ⅰ)求点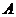 的横坐标
的横坐标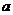 与点
与点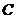 的横坐标
的横坐标
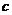 的关系式
的关系式
(Ⅱ)设曲线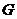 上点
上点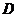 的横坐标为
的横坐标为 ,
,
求证:直线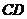 的斜率为定值.
的斜率为定值.
|
20.(本小题满分13分)
在医学生物学试验中,经常以果蝇作为试验对象.一个关有6只果蝇的笼子里,不慎混入了两只苍蝇(此时笼内共有8只蝇子,6只果蝇和2只苍蝇),只好把笼子打开一个小孔,让蝇子一只一只地往外飞,直到两只苍蝇都飞出,再关闭小孔.以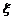 表示笼内还剩下的果蝇的只数.
表示笼内还剩下的果蝇的只数.
(Ⅰ)写出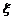 的分布列(不要求写出计算过程);
的分布列(不要求写出计算过程);
(Ⅱ)求数学期望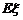 ;
;
(Ⅲ)求概率 .
.
21.(本小题满分14分)
某国采用养老储备金制度.公民在就业的第一年就交纳养老储备金,数目为 ,以后每年交纳的数目均比上一年增加
,以后每年交纳的数目均比上一年增加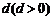 ,因此,历年所交纳的储备金数目
,因此,历年所交纳的储备金数目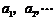 是一个公差为
是一个公差为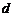 的等差数列.与此同时,国家给予优惠的计息政策,不仅采用固定利率,而且计算复利.这就是说,如果固定年利率为
的等差数列.与此同时,国家给予优惠的计息政策,不仅采用固定利率,而且计算复利.这就是说,如果固定年利率为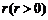 ,那么,在第
,那么,在第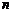 年末,第一年所交纳的储备金就变为
年末,第一年所交纳的储备金就变为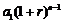 ,第二年所交纳的储备金就变为
,第二年所交纳的储备金就变为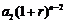 ,
, .以
.以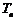 表示到第
表示到第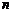 年末所累计的储备金总额.
年末所累计的储备金总额.
(Ⅰ)写出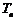 与
与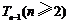 的递推关系式;
的递推关系式;
(Ⅱ)求证: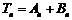 ,其中
,其中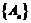 是一个等比数列,
是一个等比数列,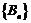 是一个等差数列.
是一个等差数列.