
1、(磨中)等差数列中,a1=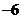 ,an=0,公差d ∈N*,则n(n>3)的最大值是( )
,an=0,公差d ∈N*,则n(n>3)的最大值是( )
A、5 B、6 C、7 D、8
2、(案中)函数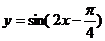 的图象可由
的图象可由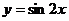 的图象按
的图象按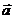 平移得到,则
平移得到,则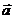 =( )
=( )
A、(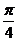 ,0)
B、 (
,0)
B、 (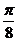 ,0)
C、 (
,0)
C、 (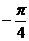 ,0)
D、 (
,0)
D、 (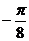 ,0)
,0)
3、(石中)设a,b,c是空间三条直线,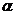 ,
,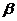 是空间两个平面,则下列命题中,逆命题不成立的是
是空间两个平面,则下列命题中,逆命题不成立的是
A、当c⊥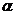 时,若c⊥
时,若c⊥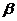 ,则
,则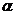 ∥
∥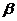
B、当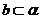 时,若b⊥
时,若b⊥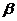 ,则
,则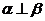
C、当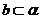 ,且c是a在
,且c是a在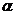 内的射影时,若b⊥c,则a⊥b
内的射影时,若b⊥c,则a⊥b
D、当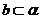 ,且
,且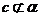 时,若c∥
时,若c∥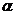 ,则b∥c
,则b∥c
4、(蒲中)函数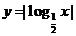 的定义域为[a,b],值域为[0,2],则b-a的取值范围是______________.
的定义域为[a,b],值域为[0,2],则b-a的取值范围是______________.
5、(一中) 已知函数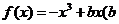 为常数)在区间(0,1)上单调递增,且方程
为常数)在区间(0,1)上单调递增,且方程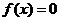 的根都在区间[-2,2]内,则
的根都在区间[-2,2]内,则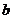 的取值范围是
的取值范围是
6、(江中) 先后抛掷两枚均匀的正方体馓子(它们的六个面分别标有点数1,2,3,4,5,6)馓子朝上的面的点数分别为X,Y 那么X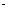 Y与X+Y为偶数的概率分别为:( )
Y与X+Y为偶数的概率分别为:( )
A、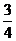 ,
, B、
B、 ,
, C、
C、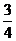 ,
,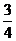 D、
D、 ,
,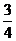
高中数学练习二
1、(西中)设P={x|x=a2+2a+1,a∈R},Q={y|y=b2+2b-2,b∈R},则P与Q的关系是( )
A、P=Q
B、P Q
C、Q
Q
C、Q P
D、P∩Q=
P
D、P∩Q=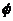
2、(丁中) 设 ,
,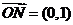 ,则满足条件
,则满足条件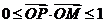 ,
,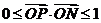 的动点P的变化范围(图中阴影部分含边界)是(
)
的动点P的变化范围(图中阴影部分含边界)是(
)

A B C D
3、(一中)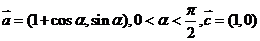 ,则
,则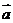 与
与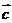 的夹角为(
)
的夹角为(
)
A、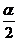 B、
B、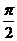 -
-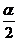 C、
C、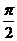 +
+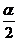 D、
D、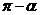
4、(蒲中)已知函数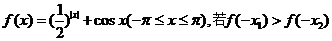 ,则有(
)
,则有(
)
A、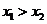 B、
B、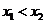 C、
C、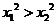 D、
D、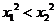
5、(石中)已知直线a、b和平面α、β,试利用上述四个元素并借助于它们之间的位置关系构造一个判断α∥β的真命题__________________________.
6、(搬中)北京《财富》全球论坛期间,某高校有14名志愿者参加接待工作.若每天排早、中、晚三班,每班4人,每人每天最多值一班,则开幕式当天不同的排班种数为_______________________.
高中数学练习三
1、(搬中)6名同学分到3个班级,每班分2名,其中甲必须分到一班,乙和丙不能分到三班,则不同的分法有( )
A、9种 B、12种 C、14种 D、18种
2、(蒲中)设M=
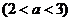 ,N=
,N=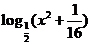 ,
,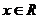 ,则M、N的大小关系是(
)
,则M、N的大小关系是(
)
A、M>N B、M=N C、M<N D、不能确定
3、(磨中)数列{an}中,a1=p,an+1= an+3,则此数列的通项公式为an=(
)
an+3,则此数列的通项公式为an=(
)
A、6+ B、6-
B、6-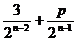
C、6-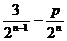 D、6+
D、6+
4、(丁中)已知F2是椭圆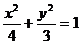 的右焦点,点A 的坐标为(1,1),那么椭圆上使2|MF2|+|MA|的值最小的点M的坐标是( )
的右焦点,点A 的坐标为(1,1),那么椭圆上使2|MF2|+|MA|的值最小的点M的坐标是( )
A、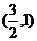 B、
B、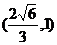 C、
C、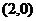 D、
D、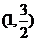
5、(一中)已知直线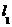 为曲线
为曲线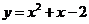 在点(1,0)处的切线,
在点(1,0)处的切线, 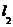 为该曲线另一条切线,且
为该曲线另一条切线,且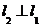 ,则直线
,则直线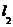 的方程为
的方程为
6、(石中)如图,在正三棱锥P-ABC中,E、F分别为棱PA、AB的中点,EF⊥CE且BC=1,则此正三棱锥的体积是
A、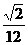 B、
B、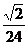 C、
C、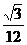 D、
D、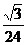
高中数学练习四
1、(蒲中)已知函数y=f(x),则集合{(x,y)|y=f(x)}∩{(x,y)|x=a}的元素个数为
A、0 B、1 C、0或1 D、以上都不对
2、(案中)当0<x<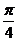 时,函数
时,函数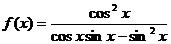 的最小值为 ( )
的最小值为 ( )
A、4
B、 C、2
D、
C、2
D、
3、(薛中)直线L: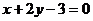 与圆C:
与圆C: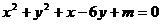 有两个交点A、B,O为坐标原点,若
有两个交点A、B,O为坐标原点,若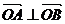 ,则
,则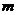 的值是( )
的值是( )
A、2
B、3 C、-1
D、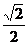
4、(石中)正方体ABCD-A1B1C1D1 中,E、F分别是AB、CC1的中点,则异面直线A1C与EF所成角的余弦值为
A.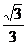 B.
B.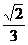 C.
C. D.
D.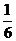
5、(西中)设P={x| x=6k一4,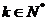 ,k≤6}
,Q={
x | x=2k,
,k≤6}
,Q={
x | x=2k,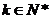 ,k≤6},则P∩Q等于___________.
,k≤6},则P∩Q等于___________.
6、(搬中)若集合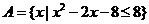 ,
,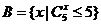 ,则
,则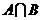 中元素有___个。
中元素有___个。
高中数学练习五
1、(丁中)已知两定点F1,F2,且|F1F2|=1,动点M满足|MF1|+|MF2|=1,则M点的轨迹是( )
A、圆 B、椭圆 C、线段 D、直线
2、(如中)不等式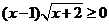 的解集(
)
的解集(
)
A、{x|x>1} B、{x|x≥1}
C、{x|x≥1或x=-2} D、{x|x≥-2或x≠1}
3、(薛中)已知A(1,2),B(4,2),则向量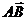 按向量
按向量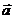 =(-1,3)平移后
=(-1,3)平移后
得到的向量坐标是( )
A、(3,0) B、(3,5) C、(-4,3) D、(2,3)
4、(石中)在正方体ABCD-A B
B C
C D
D ,O是底面ABCD的中心,M、N分别是棱DD
,O是底面ABCD的中心,M、N分别是棱DD 、D
、D C
C 的中点,则直线OM( )
的中点,则直线OM( )
A、是AC和MN的公垂线 B、垂直于AC但不垂直于MN
C、垂直于MN,但不垂直于AC D、与AC、MN都不垂直
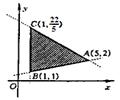
5、(一中)已知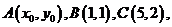 如果一个线性规划问题的可行域是
如果一个线性规划问题的可行域是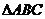 边界及其内部,线性目标函数
边界及其内部,线性目标函数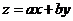 ,在B处取得最小值3,在C处取得最大值12,则下列关系一定成立的是 (
)
,在B处取得最小值3,在C处取得最大值12,则下列关系一定成立的是 (
)
A、 B、
B、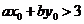 C、
C、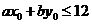 D、
D、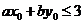
6、(搬中)某城市在中心广场建造一个花圃,花圃分为6个部分(如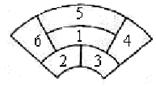 图)。现要栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花,不同的栽种方法有_______种。(以数字作答)
图)。现要栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花,不同的栽种方法有_______种。(以数字作答)
高中数学练习六
1、(一中)函数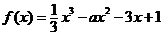 的导函数
的导函数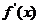 在区间[0,1]上存在反函数的充要条件是( )
在区间[0,1]上存在反函数的充要条件是( )
A. B.
B. 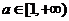
C.  D.
D.
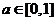
2、(蒲中)二次函数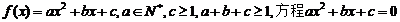 有两个小于1的不等正根,则
有两个小于1的不等正根,则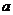 的最小值为(
)
的最小值为(
)
A、2 B、3 C、4 D、5
3、(石中)已知四个命题:①各侧面都是正方形的棱柱一定是正棱柱 ②有两个侧面是矩形的四棱柱一定是长方体 ③有一条侧棱与底面垂直的棱柱是直棱柱 ④有两条侧棱都垂直于底面一边的平行六面体是直平行六面体.则上述命题中
A、四个都是假命题 B、只有③是真命题
C、只有①是假命题 D、只有④是假命题
4、(丁中) 已知P是以F1,F2为焦点的椭圆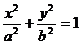
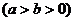 上的一点,若
上的一点,若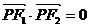 ,
,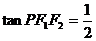 ,则此椭圆的离心率是(
)
,则此椭圆的离心率是(
)
A、 B、
B、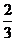 C、
C、 D、
D、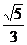
5、(薛中)若对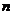 个向量
个向量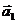 ,
,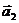 ,
, 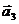 ,……,
,……, 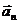 ,存在
,存在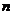 个不全为零的实数
个不全为零的实数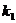 ,
,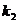 ,
,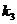 ,……,
,……,  ,使得
,使得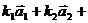
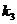
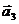 + ……+
+ ……+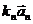 =
=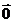 成立,则称
成立,则称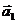 ,
,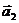 ,
, 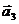 ,……,
,……,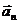 为“线性相关”,依此规定,能使
为“线性相关”,依此规定,能使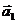 =(1,0),
=(1,0),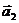 =(1,-1),
=(1,-1),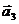 =(2,2)“线性相关”的实数
=(2,2)“线性相关”的实数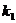 ,
,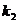 ,
,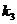 依次可取
。
依次可取
。
6、(搬中) 若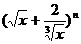 展开式中存在常数项,则n的值可以是_________.
展开式中存在常数项,则n的值可以是_________.
高中数学练习七
1、(丁中)过点(1,3)作直线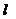 ,若
,若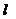 经过点(a,0)和(0,b)且
经过点(a,0)和(0,b)且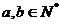 ,则可以作出
,则可以作出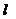 的条数为( )
的条数为( )
A、1 B、2 C、3 D、4
2、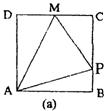 (蒲中)如图a,点P在边长为1的正方形的边上运动,
(蒲中)如图a,点P在边长为1的正方形的边上运动,
设M是CD边的中点,则点P沿着A→B→C→M运动时,以点P经过的路程x为自变量,三角形APM的面积为y的函数y=f(x),它的图象开头大致是( )
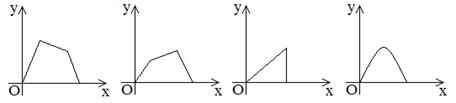
A B C D
3、(一中)不等式组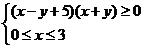 表示的平面区域是( )
表示的平面区域是( )
A、矩形 B、三角形 C、直角梯形 D、等腰梯形
4、(石中)已知平面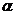 ∥平面
∥平面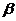 ,直线
,直线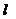
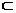 平面
平面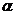 ,点P
,点P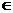 直线
直线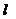 ,平面
,平面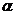 、
、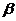 间的距离为8,则在
间的距离为8,则在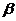 内到点P的距离为10,且到
内到点P的距离为10,且到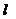 的距离为9的点的轨迹是( )
的距离为9的点的轨迹是( )
A、一个圆 B、四个点 C、两条直线 D、两个点
5、(西中)已知集合M={1,2,a},P=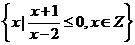 ,集合0∈M∩P,若M∪P=S,则集合S的真子集个数是
,集合0∈M∩P,若M∪P=S,则集合S的真子集个数是
6、(搬中)若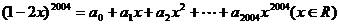 ,
,
则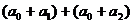 +
+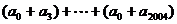 =________(用数字作答)。
=________(用数字作答)。
高中数学练习八
1、(蒲中)集合P{(x, y)|y=k}, Q={(x,y)|y=ax+1, a>0, a≠1},已知P∩Q只有一个子集,那么实数k的取值范围是
A、(-∞,1) B、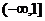 C、(1,+∞) D、R
C、(1,+∞) D、R
2、(丁中)已知双曲线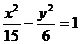 的焦点为F1,F2,点P在双曲线上,如果PF1的中点在y轴上,则|PF1|是|PF2|的( )
的焦点为F1,F2,点P在双曲线上,如果PF1的中点在y轴上,则|PF1|是|PF2|的( )
A、5倍 B、6倍 C、7倍 D、8倍
3、(磨中)设{an}(n∈N*)是等差数列,Sn是其前n项的和,且S5<S6,S6=S7>S8,则下列结论错误的是( )
A、d<0 B、a7=0 C、S9>S5 D、S6与S7均为Sn的最大值
4、(西中)命题甲: 或
或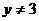 ;命题乙:
;命题乙: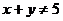 ,则(
)
,则(
)
A、甲是乙的充分非必要条件; B、甲是乙的必要非充分条件;
C、甲是乙的充要条件; D、甲既不是乙的充分条件,也不是乙的必要条件.
5、(江中)某人有两盒火柴,每盒都有n根,每次用火柴时他从两盒中任取一盒并从中抽出一根,那么他用完一盒而另一盒还有r根(1≤r≤n)的概率为:
A、C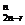 (
( )
)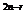 B、C
B、C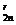 (
( )
)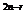
C、C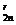 D、C
D、C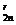
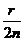
6、(石中)如图E、F分别为正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是________________(要求:把可能的图的序号都填上).
 高中数学练习九
高中数学练习九
1、(薛中)设O、A、B、C为平面上四个点,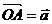 ,
,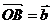 ,
,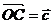 ,且
,且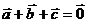 ,
,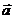 、
、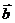 、
、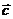 两两数量积都为-1,则
两两数量积都为-1,则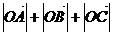 等于( )
等于( )
A、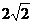 B、
B、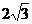 C、
C、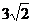 D、
D、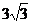
2、(磨中) 等差数列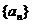 的公差为d,前n项的和为Sn,当首项a1和d变化时
的公差为d,前n项的和为Sn,当首项a1和d变化时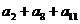 是一个定值,则下列各数中也为定值的是( )
是一个定值,则下列各数中也为定值的是( )
A、S7 B、S8 C、S13 D、S15
3、(丁中) 已知A(--2,0)、B(2,0),点C、D满足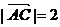 ,
,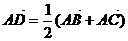
则D点的轨迹方程是( )
A、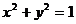 B、
B、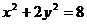 C、
C、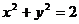 D、
D、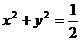
4、(如中)设n为满足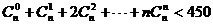 的最大自然数,则n等于
的最大自然数,则n等于
A、4 B、5 C、6 D、7
5、(蒲中)已知关于x的函数f(x)=ax2+bx+c(a、b、c为常数,且a、b≠0),若f(x1)=f(x2) (x1≠x2),则f(x1+x2)的值等于______________
6、(案中)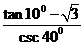 =
=
高中数学练习十
1、(丁中)设P是抛物线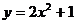 上的动点,点A(0,-1),点M在直线PA上,且点M分
上的动点,点A(0,-1),点M在直线PA上,且点M分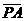 所成的比为2:1,则点M的轨迹方程为(
)
所成的比为2:1,则点M的轨迹方程为(
)
A、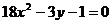 B、
B、
C、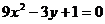 D、
D、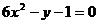
2、(石中)正方体ABCD-A B
B C
C D
D 中,点P在侧面BCC
中,点P在侧面BCC B
B 及其边界上运动,并且总保持AP⊥BD
及其边界上运动,并且总保持AP⊥BD ,则动点P的轨迹( )
,则动点P的轨迹( )
A、线段B C
B、BB
C
B、BB 的中点与CC
的中点与CC 中点连成的线段
中点连成的线段
C、线段BC D、CB中点与B
D、CB中点与B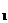 C
C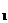 中点连成的线段
中点连成的线段
3、(西中)下列判断错误的是( )
A、命题“若q则p”与命题“若非p则非q”互为逆否命题
B、“am2<bm2”是“a<b”的充要条件
C、“矩形的两条对角线相等”的否命题为假命题
D、命题“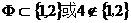 ”为真命题
”为真命题
4、(案中)已知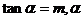 为第二象限角,则
为第二象限角,则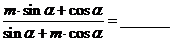
5、(蒲中)设f(x)是定义在R上的最小正周期为T的函数,则f(3x+5)是( )
A、最小正周期为 的函数
B、最小正周期为3T的函数
的函数
B、最小正周期为3T的函数
C、最小正周期为T的函数 D、最小正周期为5T的函数
6、(一中)曲线y=x3+3x2+6x-10的切线中,斜率最小的切线方程是
高中数学练习十一
1、(西中)如果a、b是实数,那么“|a|<1,|b|<1”是“|a+b|+|a-b|<2”的( )
A、充分不必要条件 B、必要不充分条件
C、充要条件 D、既不充分又不必要条件
2、(一中)已知集合M=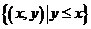 ,P=
,P=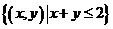 ,S=
,S=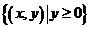 ,若
,若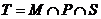 ,点
,点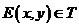 ,则
,则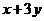 的最大值是
( )
的最大值是
( )
A、0 B、2 C、3 D、4
3、(石中)在正方体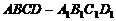 中,EF是异面直线AC和
中,EF是异面直线AC和 的公垂线,则EF和
的公垂线,则EF和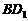 的关系是( )
的关系是( )
A、相交不垂直 B、相交垂直
C、异面直线 D、互相平行
4、(如中)在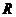 上定义运算
上定义运算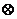 :
: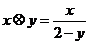 ,若关于
,若关于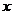 的不等式
的不等式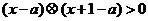 的解集是集合
的解集是集合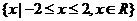 的子集,则实数
的子集,则实数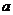 的取值范围是
的取值范围是
A、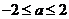 B、
B、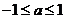 C、
C、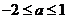 D、
D、
5、(薛中)设平面内有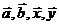 四个向量,满足
四个向量,满足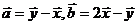 ,
,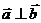 ,
,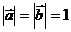 ,设
,设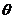 为
为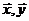 的夹角,则
的夹角,则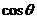 =_______.
=_______.
6、(蒲中)函数f(x)=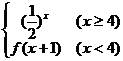 ,则f(log23)=_________
,则f(log23)=_________
高中数学练习十二
1、(江中)拟发行体育奖券,号码从000001到999999,购买时揭号对奖,若规定:从个位数起,第一、三、五位是不同的奇数,第二、四、六位均为偶数时为中奖号码,则中奖率为( )?(精确到0.01%)
A、2.5% B、0.25% C、0.75% D、7.5%
2、(西中)集合P={1,4,9,16,……},若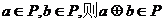 ,则运算
,则运算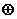 可能是(
)
可能是(
)
A、加法 B、减法 C、乘法 D、除法
3、(蒲中)已知定义在R上的函数y=f(x)满足下列三个条件:
(1)对任意的x∈R都有f(x+4)=f(x);(2)对任意的0≤x1<x2≤2,都有f(x1)<f(x2);(3)y=f(x+2)的图象关于y轴对称,则下列结论中正确的是
A、f(4.5)<f(6.5)<f(7) B、f(4.5)<f(7)<f(6.5)
C、f(7)<f(4.5)<f(6.5) D、f(7)<f(6.5)<f(4.5)
4、(案中)在△ABC中,已知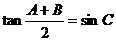 ,则
,则
①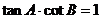 ②
②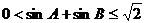
③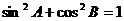 ④
④
正确的命题序号为
5、(西中)设集合M={x|2x2-5x-3=0},N={x|mx=1},若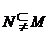 ,则实数m的取值集合为________________ 。
,则实数m的取值集合为________________ 。
6、(石中)用铁条焊接一个棱长为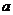 的正方体骨架,在其内部放置一个气球并对其充气,使其膨胀成尽可能大的一个球。若不计铁条的粗细,则此时气球的表面积为___________
的正方体骨架,在其内部放置一个气球并对其充气,使其膨胀成尽可能大的一个球。若不计铁条的粗细,则此时气球的表面积为___________
高中数学练习十三
1、(丁中)直线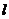 1,
1,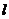 2分别过点P(--2,3)、Q(3,-2),它们分别绕点P、Q旋转但保持平行,那么它们之间的距离d的取值范围是(
)
2分别过点P(--2,3)、Q(3,-2),它们分别绕点P、Q旋转但保持平行,那么它们之间的距离d的取值范围是(
)
A、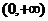 B、
B、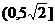 C、
C、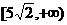 D、
D、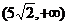
2、(蒲中)函数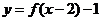 是奇函数,则函数
是奇函数,则函数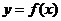 的图象关于 (
)
的图象关于 (
)
A、直线 x=-2对称 B、直线 x=2对称
C、点(2,-1)对称 D、点(-2,1)对称
3、(如中)不等式(x-2)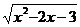 ≥0的解集是_________________.
≥0的解集是_________________.
4、(搬中)由等式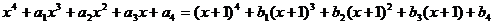
定义映射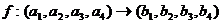 ,则f(4,3,2,1)=
,则f(4,3,2,1)=
5、(西中)已知命题P: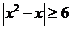 ,命题Q:
,命题Q: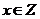 ,且“P且Q”与“非Q”同时为假命题,则
,且“P且Q”与“非Q”同时为假命题,则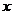 的值等于
。
的值等于
。
6、(石中)在正方体ABCD-A1B1C1D1中,下面给出四个命题:
①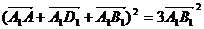
②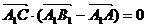
③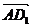 与
与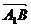 的夹角为600
的夹角为600
④此正方体的体积为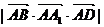 。
。
其中错误命题的序号为_______________。
高中数学练习十四
1、(西中)已知集合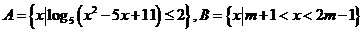 ,若
,若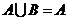 ,则( )
,则( )
A、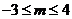 B、
B、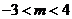 C、
C、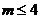 D、
D、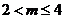
2、(蒲中)已知函数f(x)=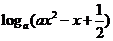 在[1,
在[1,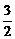 ]上恒正,则实数a的取值范围是( )
]上恒正,则实数a的取值范围是( )
A、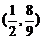 B、
B、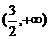 C、
C、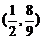 ∪
∪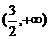 D、
D、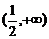
3、(如中)设 ,
,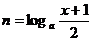 ,
,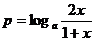 ,其中
,其中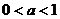 ,
,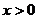 且
且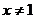 ,则下列各式中正确的是
,则下列各式中正确的是
A、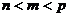 B、
B、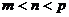 C、
C、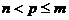 D、
D、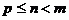
4、(丁中)已知点M(-3,0),N(3,0),B(1,0),圆C与直线MN切于点B,过M、N与圆C相切的两直线相交于点P,则P点的轨迹方程为( )
A、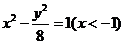 B、
B、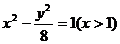
C、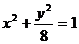 (x
> 0) D、
(x
> 0) D、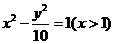
5、(石中)以一个正方体的顶点为顶点的四面体的个数是
6、(磨中)已知数列{an}(n∈N*)是首项为a1,公比为q的等比数列,则
a1C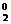 -a2C
-a2C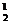 +a3C
+a3C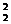 =_________________,
=_________________,
a1C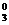 -a2C
-a2C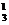 +a3C
+a3C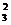 -a4C
-a4C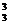 =______________
=______________
由上述结果归纳概括出关于正整数n的一个结论是______________________
高中数学练习十五
1、(西中)设集合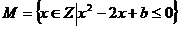 有且只有一个元素,则
有且只有一个元素,则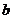 的取值范围是( )
的取值范围是( )
A、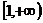 B、
B、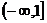 C、
C、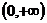 D、
D、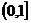
2、(丁中)动直线y=k(x-4)交y2=4x于M、N两点,O为坐标原点,则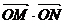 =( )
=( )
A、0 B、1 C、2 D、3
3、(蒲中)不等式|2x-log2x|<2x+|log2x|成立,则x的范围是( )
A、0<x<1 B、1<x<2 C、x>1 D、x>2
4、(江中)国际上通常用恩格尔系数来衡量一个国家和地区人民生活水平状况,它的计算公式是: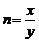 (x:人均食品支出总额,y:人均个人消费支出总额),且y=2x+475,各种类型家庭:
(x:人均食品支出总额,y:人均个人消费支出总额),且y=2x+475,各种类型家庭:
|
家庭类型 |
贫困 |
温饱 |
小康 |
富裕 |
|
n |
n≥59% |
50%≤n<59% |
40%≤n<50% |
30%≤n<40% |
李先生居住地2002年比1998年食品价格下降了7.5%,该家庭在2002年购买食品和1998年完全相同的情况下人均少支出75元,则该家庭2002年属于( )
A、贫困 B、温饱 C、小康 D、富裕
5、(石中)一个人在山水相连的湖边游玩,当他走到一山坡上,此时其水平视线高出湖水面5m, 正要观看水中景色时,突然发现水中有只老鹰,此时他观看的俯角约为60°, 他马上抬头搜索,看到此老鹰仰角约为45°,那么此时老鹰距水面约 m 。
6、(一中)曲线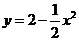 与
与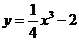 在交点处的切线夹角
。
在交点处的切线夹角
。
高中数学练习十六
1、(如中)不等式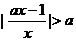 的解集为M,且2
的解集为M,且2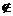 M,则
M,则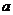 的取值范围为
的取值范围为
A、 B、
B、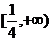 C、
C、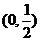 D、
D、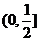
2、(蒲中)若函数f(x)=ax2+b|x|+c(a≠0)的定义域R分成四个单调区间,则实数a,b,c满足( )
A、b2-4ac>0且a>0 B、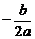 >0
>0
C、b2-4ac>0
D、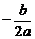 <0
<0
3、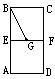 (石中)如图所示,矩形ABCD中,AB=2AD,E、F、G分别是AB、CD、EF的中点,把矩形沿EF折成60°的二面角,则异面直线AE和BG所成角为(
)
(石中)如图所示,矩形ABCD中,AB=2AD,E、F、G分别是AB、CD、EF的中点,把矩形沿EF折成60°的二面角,则异面直线AE和BG所成角为(
)
A、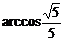 B、
B、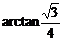
C、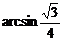 D、
D、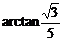
4、(搬中)用1、2、3、4、5、6、7、8组成没有重复数字的八位数,要求1和2相邻,3与4相邻,5与6相邻,而7与8不相邻,这样的八位数共有 ______________个(用数字作答)
5、(丁中)⊿ABC中,两边对应的向量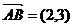 ,
, 。若三角形ABC是直角三角形,则实数k的值为___________________。
。若三角形ABC是直角三角形,则实数k的值为___________________。
6、(案中)已知α+β=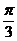 ,且
,且 (tanαtanβ+c)+tanα=0(c为常数),那么tanβ=
(tanαtanβ+c)+tanα=0(c为常数),那么tanβ=
高中数学练习十七
1、(丁中)已知点A(1,0,0),B(0,1,0),C(0,0,1),若存在点D使得DB∥AC,DC∥AB,则点D的坐标为( )
A、(-1,1,1) B、(-1,1,1)或(1,-1,-1)
C、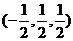 D、
D、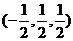 或(1,-1,-1)
或(1,-1,-1)
2、(丁中)双曲线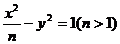 的两个焦点为F1,F2,P在双曲线上,且满足|PF1|+|PF2|=
的两个焦点为F1,F2,P在双曲线上,且满足|PF1|+|PF2|=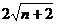 ,则⊿PF1F2的面积为( )
,则⊿PF1F2的面积为( )
A、1 B、2 C、3 D、4
3、(磨中)已知数列{an}的前n项和为Sn=3n-C,则C=1,是{an}为等比数列的( )
A、充分不必要条件 B、必要不充分条件
C、充要条件 D、既不充分也不必要条件
4、(蒲中)已知映射f:A→B,其中A=B=R,对应法则f:y= -x2+2x,对于实数k∈B,在集合A中不存在原象,则k的取值范围是( )
A、k>1 B、k≥1
C、k<1 D、k≤1
5、(如中)若不等式2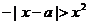 至少有一个负解,则参数
至少有一个负解,则参数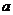 的取值范围是
的取值范围是
A、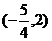 B、
B、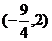 C、
C、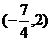 D、
D、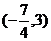
6、(搬中)有10个不同的球,其中2个红球,5个黄球,3个白球,若取到一个红球得5分,若取到一个黄球得1分,取到一个白球得2分,从中取出5个球,使总分大于10分且小于15分的取法种数为
 高中数学练习十八
高中数学练习十八
1、(搬中)四个不同的小球放入编号为1,2,3,4的四个盒子中,则恰有一个空盒的放法共有_____种(用数字作答)。
2、(丁中)抛物线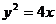 的焦点为F,准线
的焦点为F,准线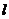 交X轴于R点,过抛物线上一点P(4,4)作PQ⊥
交X轴于R点,过抛物线上一点P(4,4)作PQ⊥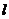 于Q,则梯形PQRF的面积为( )
于Q,则梯形PQRF的面积为( )
A、12 B、14 C、16 D、18
3、(蒲中)已知函数f(x),则函数f(x+1)的反函数是( )
A、f-1(x+1) B、f-1(x-1) C、f-1(x)+1 D、f-1(x)-1
4、(石中)如果直线l、m与平面α、β、γ满足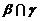 =l,
=l,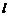 ∥α,
∥α,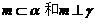 ,那么必有( )
,那么必有( )
A、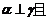
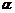 ∥
∥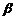 B、
B、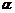
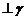 且m∥
且m∥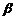
C、m∥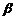 且
且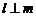 D、
D、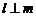 且
且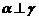
5、(搬中)0.98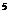 的近似值是____
__ (精确到0.001)
的近似值是____
__ (精确到0.001)
6、 (如中)不等式
(如中)不等式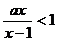 的解集为{
的解集为{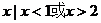 },则不等式
},则不等式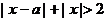 的解集为________________.
的解集为________________.
高中数学练习十九
1、(蒲中)已知函数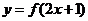 是偶函数,则一定是函数
是偶函数,则一定是函数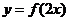 图象的对称轴的直线是
图象的对称轴的直线是
A、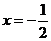 B、
B、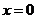 C、
C、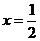 D、
D、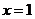
2、(如中)已知两正数x,y
满足x+y=1,则z=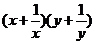 的最小值为
的最小值为
3、(搬中)有两排座位,前排11个座位,后排12个座位,现安排2人就座,规定前排中间的3个座位不能坐,并且这2人不左右相邻,那么不同排法的种数是________。
4、(案中)设 均为锐角,且
均为锐角,且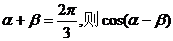 的取值范围为( )
的取值范围为( )
A、(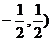 B、[
B、[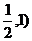
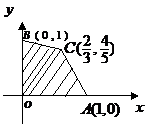 C、(
C、( D、(
D、(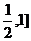
5、(一中)给出平面区域如图所示目标函数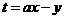 ,当且仅当
,当且仅当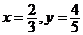 时,目标函数
时,目标函数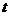 取
取
最小值,则实数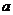 的取值范围
的取值范围
6、(丁中)双曲线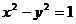 左支上一点
左支上一点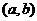 到其渐近线
到其渐近线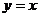 的距离为
的距离为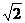 ,
,
则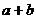 的值为_______。
的值为_______。
高中数学练习二十
1、(磨中)数列{Xn}满足x1=1,x2=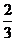 ,且
,且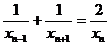 (n≥2),则xn=(
)
(n≥2),则xn=(
)
A、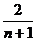 B、
B、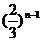 C、
C、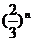 D、
D、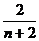
2、(江中)选手A与另一位实力相当的对手B比赛,设两次比赛中A胜两次的概率为P1,4次比赛中A胜3次的概率为P2,8次比赛中A胜5次的概率为P3,则( )
A、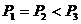 B、
B、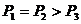
C、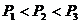 D、
D、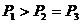
3、(蒲中)设f(x)是R上以2为周期的奇函数,已知当x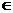 (0,1)时,f(x)=log2
(0,1)时,f(x)=log2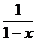 ,则f(x)在(1,2)上是( )
,则f(x)在(1,2)上是( )
A、增函数且f(x)<0 B、增函数且f(x)>0
C、减函数且f(x)<0 D、减函数且f(x)>0
4、(薛中)A、B是非原点的两点,C点满足以下条件,则A、B、C三点共线是
①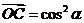

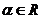
②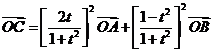
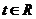
③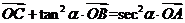 (
(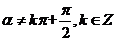 )
)
A、①② B、 ②③ C、①③ D、①②③
5、(丁中)直线l过点A(0,-1),且点B(-2,1)到l距离是点C(1,2)到l的距离的两倍,则直线l的方程是 。
6、(搬中)若n为奇数,则7 n+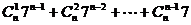 被9除得余数是
被9除得余数是
高中数学练习二十一
1、(案中)若向量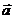 =
=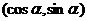 ,
,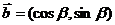 ,则
,则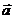 与
与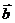 一定满足( )
一定满足( )
A、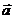 与
与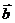 的夹角为
的夹角为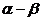 B、
B、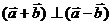
C、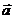 ∥
∥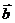 D、
D、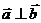
2、(磨中) 在数列{an}中,已知a1 = 1, 且当n ≥2时,a1a2 … an = n2,则a3 + a5等于( )
A、 B、
B、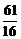 C、
C、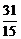 D、
D、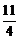
3、(如中)当点P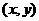 在正方形
在正方形 ,
,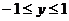 内运动变化时,点M
内运动变化时,点M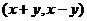 的变化区域的面积为( )
的变化区域的面积为( )
A、4 B、8 C、16 D、不存在
4、(搬中)某餐厅供应客饭,每位顾客可以在餐厅提供的菜肴中任选2荤2素共4种不同的品种,现在餐厅准备了五种不同的荤菜,若要保证每位顾客有200种以上不同选择,则餐厅至少还需准备不同的素菜品种( )种
A、10 B、9 C、8 D、7
5、(蒲中)已知函数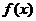 同时满足五个条件:
同时满足五个条件:
①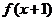 的定义域是[-5,3]; ②
的定义域是[-5,3]; ②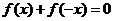 ; ③f(-1)=0;
; ③f(-1)=0;
④在[-4,0)上单调递减; ⑤没有最大值.
则不等式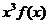 ≤0的解集是 .
≤0的解集是 .
6、(如中)已知a>b>0,求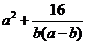 的最小值.
的最小值.
高中数学练习二十二
1、(蒲中)一天清晨,某同学生病了,体温上升,吃过药后感觉好多了,中午时他的体温基本正常,但是下午他的体温又开始上升,直到半夜才感觉身上不那么发烫了。下面大致能上反映出该同学这一天(0时-24时)体温的变化情况的图是

A B C D
2、(如中)对于满足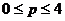 的实数P,使
的实数P,使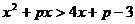 恒成立的
恒成立的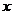 的取值范围是_________________.
的取值范围是_________________.
3、(石中)四棱锥P-ABCD的底面ABCD是一个正方形,PD⊥面ABCD,则这个四棱锥的五个面内,互相垂直的平面共有( )
A、3对 B、4对 C、5对 D、6对
4、(蒲中)y=log2(2x+4)(x>-2)图象经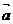 平移后得到图象对应的解析式为y=log2x,则( )
平移后得到图象对应的解析式为y=log2x,则( )
A、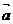 =(-2,1) B、
=(-2,1) B、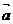 =(-2,-1)
C、
=(-2,-1)
C、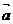 =(2,-1) D、
=(2,-1) D、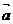 =(2,1)
=(2,1)
5、(丁中)过椭圆的左焦点F且倾斜角为60°的直线交椭圆于A、B两点,若|AF|=2|BF|,则此椭圆的离心率为______________。
6、(磨中)等差数列{an}中,a1=a (a≠0) ,a2=b 则该数列中恰有一项为0的充要条件是( )
A、a-b∈N* B、a+b∈N*
C、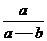 ∈N*
D、
∈N*
D、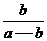 ∈N*
∈N*
高中数学练习二十三
1、(一中)设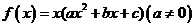 在
在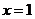 和
和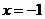 处均有极值,则下列点中一定在
处均有极值,则下列点中一定在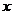 轴上的是
( )
轴上的是
( )
A、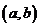 B、
B、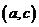 C、
C、 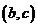 D、
D、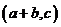
2、(磨中)已知数a1,a2,……,an为各项都大于0的等比数列,则( )
A、a1+a10>a5+a6 B、a1+a10≤a5+a6
C、a1+a10≥a5+a6 D、a1+a10与a5+a6的大小不定
3、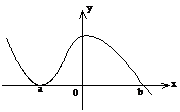 (蒲中)如图,函数y=f(x)的图象如右,
(蒲中)如图,函数y=f(x)的图象如右,
则函数y=f(x)的解析式可能为( )
A、f(x)=(x-a)2.(b-x)
B、f(x)=(x-a)2.(x+b)
C、f(x)= -(x-a)2.(x+b)
D、f(x)=(x-b)2.(x-a)
4、(丁中)已知方程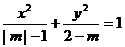 表示焦点在y轴上的椭圆,则m的取值范围是( )
表示焦点在y轴上的椭圆,则m的取值范围是( )
A、m<2 B、1<m<2
C、m<-1或1<m<2 D、m<-1或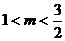
5、(丁中)设点P(x,y),其中x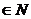 ,y
,y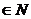 ,且满足
,且满足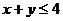 ,则点P的个数为
,则点P的个数为
___________.
6、(石中)在底面边长为1的正四棱锥中,若相邻两侧面所成的二面角为
120°,则侧棱与底面所成角的余弦值为________________.
高中数学练习二十四
1、 (案中)为了使函数y=sinωx(ω>0)在区间[0,1]上至少出现50 次最
大值,则ω的最小值是( )
A、98π B、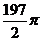 C、
C、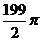 D、100π
D、100π
2、(蒲中)设函数f(x)的定义域为D,如果对于任意x1∈D,存在唯一的x2∈D,使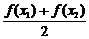 =C(C为常数)成立,则称函数y=f(x)在D上的均值为C,给出下列四个函数:①y=x3,②y=4sinx, ③y=lgx,④y=2x,则满足在其定义域上均值为2的所有函数是( )
=C(C为常数)成立,则称函数y=f(x)在D上的均值为C,给出下列四个函数:①y=x3,②y=4sinx, ③y=lgx,④y=2x,则满足在其定义域上均值为2的所有函数是( )
A、①② B、③④ C、①③④ D、①③
3、(丁中)抛物线 的顶点为
的顶点为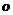 ,焦点为F,若P为此抛物线上一点,对于三角形POF的形状有下列说法:①可能是等腰三角形;②可能是等腰直角三角形;③可能是正三角形。其中正确的是( )
,焦点为F,若P为此抛物线上一点,对于三角形POF的形状有下列说法:①可能是等腰三角形;②可能是等腰直角三角形;③可能是正三角形。其中正确的是( )
A、① B、② C、①② D、①②③
4、(案中)函数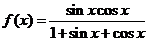 的值域为 ( )
的值域为 ( )
A、[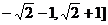 B、
B、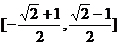
C、 D、
D、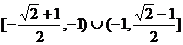
5、(蒲中)在(-1,1)内存在x0,使3ax-2a+1=0成立,则实数a的取值范围是___________
6、(搬中)17个篮球队,分成三个组(6,6,5),第一阶段,各组举行单循环比赛,第二阶段,由各组的前两名举行单循环比赛,决出冠亚军,共举行 ______场球赛;若第二阶段中,原同一组的两队免赛,共举行了 场球赛。
高中数学练习二十五
1、(石中)以等腰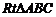 的斜边BC上的高AD为折痕,将
的斜边BC上的高AD为折痕,将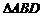 折起,使折起后的
折起,使折起后的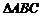 恰成等边三角形,则二面角C-AD-B等于(
)
恰成等边三角形,则二面角C-AD-B等于(
)
A、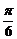 B、
B、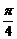 C、
C、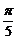 D、
D、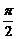
2、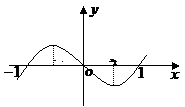 (一中)图13-4是函数
(一中)图13-4是函数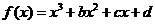
的大致图像,则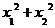 等于(
)
等于(
)
A、 B、
B、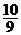 C、
C、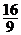 D、
D、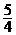
3、(如中)若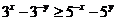 ,则(
)
,则(
)
A、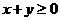 B、
B、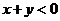 C、
C、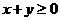 D、
D、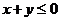
4、(丁中)已知点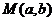 在由不等式组
在由不等式组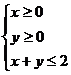 所确定的平面区域内,则点N
所确定的平面区域内,则点N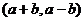 所在平面区域的面积是(
)
所在平面区域的面积是(
)
A、1 B、2 C、4 D、8
5、(丁中)与圆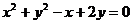 关于直线y=x+1对称的圆的方程___________
关于直线y=x+1对称的圆的方程___________
6、(案中)在△ABC中,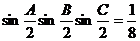 ,则△ABC的形状为
,则△ABC的形状为
高中数学练习二十六
1、(丁中)设全集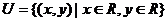 ,集合
,集合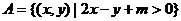 ,
,
集合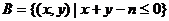 ,那么点P(2,3)
,那么点P(2,3)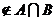 的充要条件是( )
的充要条件是( )
A、 B、
B、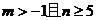
C、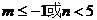 D、
D、
2、(磨中)若一个等差数列前三项的和为34,最后三项的和为146,且所有项和
为390,则这个数列的项数为( )
A、13 B、12 C、11 D、10
3、(如中)设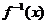 是函数
是函数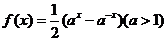 的反函数,则使
的反函数,则使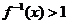 成立的
成立的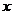 的取值范围
的取值范围
A、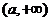 B、
B、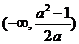 C、
C、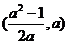 D、
D、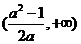
4、(蒲中)设函数f(x)是定义在R上以3为周期的奇函数,若f(1)>1,f(2)=,则 A、a< B、a< 且a≠-1
C、a> 或a<-1 D、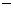 1<a<
1<a<
5、(案中)在锐角 ABC中,若C=2B,则
ABC中,若C=2B,则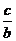 的范围是(
)
的范围是(
)
A、(0,2) B、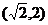 C、
C、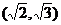 D、
D、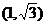
6、(丁中)已知函数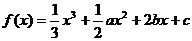 ,当
,当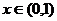 时取得极大值,当
时取得极大值,当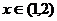 时取得极小值。那么
时取得极小值。那么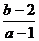 的取值范围是____________。
的取值范围是____________。
高中数学练习二十七
1、(石中)正三棱锥S-ABC的底面边长为2a,E、F、G、H分别是SA、SB、BC、AC的中点,则EFGH面积的取值范围是( )
A、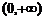 B、
B、 C、
C、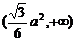 D、
D、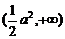
2、(丁中)已知力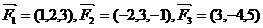 ,若
,若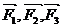 共同作用在一个物体上,使物体从点A(1,--2,1)移动到点B(3,1,2),则合力所作的功为(
)
共同作用在一个物体上,使物体从点A(1,--2,1)移动到点B(3,1,2),则合力所作的功为(
)
A、10 B、12 C、14 D、16
3、(丁中)已知A、B、C三点在曲线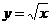 上,其横坐标依次为1
上,其横坐标依次为1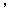
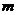
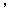 4
4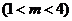 ,当△ABC的面积最大时,
,当△ABC的面积最大时,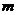 等于( ).
等于( ).
A、3 B、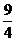 C、
C、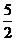 D、
D、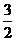
4、(薛中)设平面上有四个互异的点A、B、C、D,已知
( ,则
,则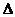 ABC的形状一定是
ABC的形状一定是
5、(蒲中)若函数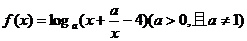 的值域为R,则实数a的取值范围是______________________
的值域为R,则实数a的取值范围是______________________
6、(江中)在100张奖券中,有4张中奖,从中任取2张,则2张都中奖的概率为
高中数学练习二十八
1、(丁中)已知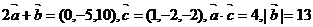 ,则
,则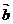 与
与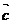 的夹角是(
)
的夹角是(
)
 A、600
B、
A、600
B、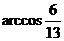 C、
C、 D、
D、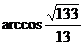
2、(一中)给出平面区域如图所示,若使目标函数z=ax+y
(a>0)取得最大值的最优解有无穷多个,则a值为( )
A、 B、
B、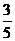 C、4 D、
C、4 D、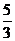
3、(丁中)四条曲线:
①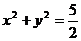 ②
②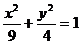 ③
③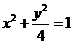 ④
④ 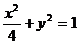
其中与直线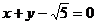 仅有一个交点的曲线是(
)
仅有一个交点的曲线是(
)
A、①②③ B、②③④ C、①②④ D、①③④
4、(案中)若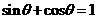 ,则对任意实数
,则对任意实数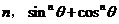 的取值为(
)
的取值为(
)
A、1 B、区间(0,1)
C、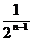 D、不能确定
D、不能确定
5、(如中)已知F1、F2分别为双曲线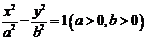 的左、右焦点,P为双曲线左支上的任意一点,若
的左、右焦点,P为双曲线左支上的任意一点,若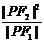 的最小值为
的最小值为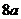 ,则双曲线的离心率e的取值范围是
,则双曲线的离心率e的取值范围是
A、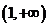 B、
B、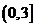 C、
C、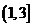 D、
D、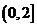
6、(蒲中)已知函数f(x)满足:f (p+q)= f (p) f (q) , f (1)=3, 则
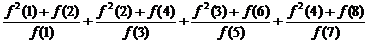 =
。
=
。
高中数学练习二十九
1、(磨中) 在等差数列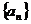 中,若
中,若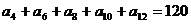 ,则
,则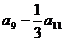 的值为( )
的值为( )
A、14 B、15 C、16 D、17
2、(蒲中)已知函数y=loga(ax2-x)在区间[2,4]上是增函数,那么a的取值范围是( )
A、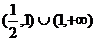 B、
B、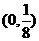 ∪
∪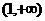 C、
C、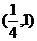 D、
D、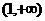
3、(蒲中)已知奇函数f(x)在[-1,0]上为单调递减函数,又α,β为锐角三角形两内角,则( )
A、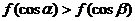 B、
B、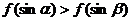
C、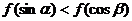
 D、
D、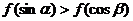
4、(薛中)已知O为原点,点A、B的坐标分别为(a,0)、(0,a), 其中a>0,点p在线段AB上,且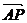 =t
=t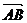 (0≤t≤1),
(0≤t≤1), 则
则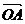
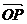 的最大值为( )
的最大值为( )
A、a B、2a
C、3a
D、a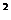
5、(丁中)点P是椭圆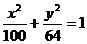 上一点,F1、F2是焦点,若∠F1PF2=600,则△F1PF2的面积为___________________。
上一点,F1、F2是焦点,若∠F1PF2=600,则△F1PF2的面积为___________________。
6、(如中)若不等式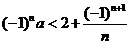 对于任意的正整数
对于任意的正整数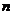 恒成立,则实数
恒成立,则实数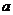 的取值范围是
的取值范围是
A、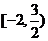 B、
B、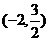 C、
C、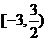 D、
D、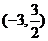
高中数学练习三十
1、(一中)函数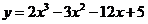 在
在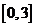 上的最大值和最小值分别为(
)
上的最大值和最小值分别为(
)
A、5;-15 B、5;-4 C、-4;-15 D、5;-16
2、(薛中)点O为△ABC所在平面上一点,且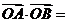

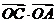 ,则点O为△ABC的( )
,则点O为△ABC的( )
A、内心 B、外心 C、重心 D、垂心
3、(石中)有下列四个命题:①过平面α外两点有且只有一个平面与平面α垂直;②互相平行的两条直线在同一平面内的射影必是平行线;③直线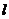 上两个不同点到平面α的距离相等是
上两个不同点到平面α的距离相等是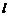 ∥α的必要非充分条件;④平面α内存在无数条直线与已知直线
∥α的必要非充分条件;④平面α内存在无数条直线与已知直线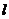 垂直是
垂直是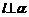 的充分非必要条件.
其中正确命题的个数是(
)
的充分非必要条件.
其中正确命题的个数是(
)
A、0 B、1 C、2 D、3
4、(蒲中)已知函数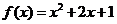 ,若存在t,当
,若存在t,当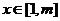 时,
时,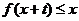 恒成立,则实数m的最大值为______________.
恒成立,则实数m的最大值为______________.
5、(丁中)直线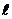 在x,y轴上截距的倒数和为常数
在x,y轴上截距的倒数和为常数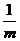 ,则直线过定点________________
,则直线过定点________________
6、(磨中)等差数列{an},{bn}的前n项和分别为Sn,Tn,若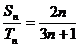 ,则
,则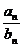 =______
=______
高中复习数学练习一参考答案
中学数学练习答案
一、C,B,B,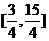 ,[3,4],A
,[3,4],A
二、B,A,A,D,若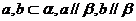 ,且a与b相交,则
,且a与b相交,则 ;或若
;或若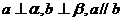 ,则
,则 ,
,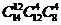
三、A,A,B,B,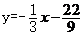 ,B
,B
四、C,A,B,B,{2,8,32},4个
五、C,C,A,A,C,120
六、C,D,B,D,{-4, 2, 1},10或5等
七、B,A,D,B,15,2004
八、B,B,C,B,A,3
九、C,C,A,C,c,-1
十、A,A,B,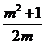 ,A,3x-y-11=0
,A,3x-y-11=0
十一、C,D,D,C,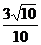 ,
,
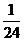
十二、C,C,B,②④,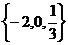 ,2
,2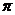 a2
a2
十三、B,D,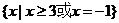 ,(0,-3,4,0),-1,0,1,2,③④
,(0,-3,4,0),-1,0,1,2,③④
十四、A,C,A,B,58,a1(1-q)2、a1(1-q)3
a1C -a2C
-a2C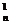 +a3C
+a3C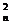 -a4C
-a4C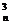 +……+(-1)n an+1C
+……+(-1)n an+1C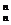 =a1(1-q)n
=a1(1-q)n
十五、D,A,C,D,10+5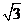 ,
,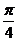
十六、B,B,A,576,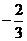 、
、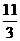 、
、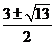 ,
,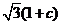
十七、A,A,C,A,B,110
十八、144,B,D,D,0.904,
十九、C,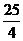 ,346,D ,
,346,D ,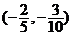 ,
,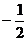
二十、A,B,A,D,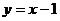 或
或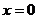 ,7
,7
二十一、B,B,B,D,[-4,-1]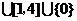 ,16
,16
二十二、C,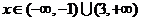 ,C,C,
,C,C,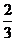 ,C
,C
二十三、A,C,A,D,15,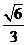
二十四、B,D,A,D,a<-1或a>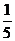 ,55、52
,55、52
二十五、D,C,C,C,(x+2)2+(y-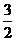 )2=
)2=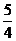 ,等边三角形
,等边三角形
二十六、C,A,D,D,C,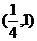
二十七、B,C,B ,等腰三角形,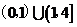 ,
,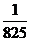
二十八、C,B,D,A,C,24
二十九、C,D,C,D,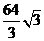 ,A
,A
三十、A ,D,B,4,(m,m),