
1、cos(-3000)等于
(A) -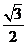 (B)-
(B)-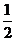 (C)
(C) 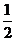 (D)
(D)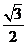
2、设全集U=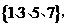 集合M=
集合M=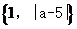 ,
, C
C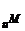 =
=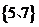 ,则实数a的值为
,则实数a的值为
(A) -2或8 (B) -8或-2 (C)2或-8 (D) 2或8
3、将直线l:2x+3y-1=0,沿向量a =(-1,-2)平移后得到直线l ,则直线 l
,则直线 l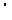 的方程是
的方程是
(A) 2x+3y-7=0 (B) 2x+3y-5=0 (C)2x+3y-3=0 (D) 2x+3y+7=0
4、已知p: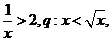 则p是q的
则p是q的
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
5、已知函数f(x)=1+logax(a>0),且a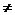 1),则f(x)的反函数f-1(x)的反函数的解析式为
1),则f(x)的反函数f-1(x)的反函数的解析式为
(A)f-1(x)=ax-1(x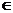 R)
(B) f-1(x)=ax-1(x
R)
(B) f-1(x)=ax-1(x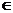 R)
R)
(C) f-1(x)=ax-1(x>1) (D) f-1(x)=ax-1(x>1)
6、等差数列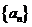 的前n项和为Sn,若
的前n项和为Sn,若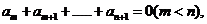 则S
则S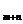 等于
等于
(A)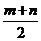 (B)
(B) 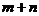 (C)0 (D) 1
(C)0 (D) 1
7、在下列关于函数y=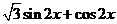 的结论中,正确的是
的结论中,正确的是
(A)
在区间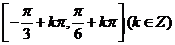 上是增函数
上是增函数
(B)
周期是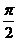
(C) 最大值为1,最小值为-1
(D) 是奇函数
8、
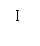
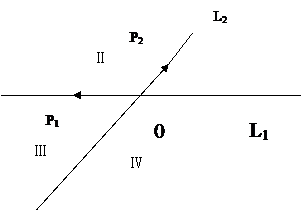 如图,平面内的两条相交直线l1和l2将该平面分割成四个部分
如图,平面内的两条相交直线l1和l2将该平面分割成四个部分 (不包括边界),向量
(不包括边界),向量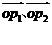 分别为l1和l2的方向向量,若
分别为l1和l2的方向向量,若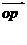 =a
=a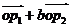 ,且点P落在第Ⅰ
,且点P落在第Ⅰ
部分,则实数a、b满足
(A) a>0 , b>0 (B) a>0 ,b<0
(C) a<0 ,b>0 (D) a<0 , b<0
9、双曲线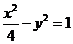 的两个焦点为F1,F2 ,点P在双曲线上,
的两个焦点为F1,F2 ,点P在双曲线上,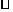
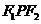 的面积为
的面积为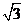 ,则
,则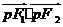 =
=
(A)2 (B)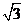 (C)-2 (D) -
(C)-2 (D) -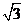
10、将正方形ABCD沿对角线AC折起,当以A、B、C、D四点为顶点的三棱锥体积最大时,异面直线AD与BC所成的角为
(A)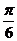 (B)
(B) (C)
(C)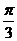 (D)
(D)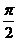
11、设0<x<1 ,a,b都为大于零的常数,则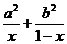 的最小值为
的最小值为
(A)(a-b)2 (B) (a+b)2 (C)a2b2 (D)a2
12、在平面区域D中任取一点,记事件“该点落在其内部一个区域d内”为事件A,则事件A发生的概率P(A)=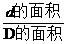 ,在区间[-1,1]上任取两点a,b,方程x
,在区间[-1,1]上任取两点a,b,方程x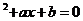 有实数根的概率为P,则
有实数根的概率为P,则
(A)0<P<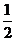 (B)
(B)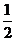 <P<
<P<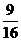
(C)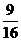 <P<
<P<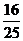 (D)
(D)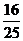 <P<1
<P<1
13、在 的展开式中,常数项是____
的展开式中,常数项是____
14、已知f(n)=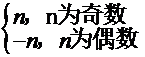 若a
若a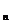 =f(n)+f(n+1),则
=f(n)+f(n+1),则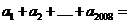 __
__
15、如图:

在
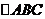 中,
中,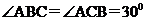 ,AB,AC边上的高分别为CD、DE,则以B、C为焦点,且经过D、E两点的椭圆与双曲线的离心率之和为________
,AB,AC边上的高分别为CD、DE,则以B、C为焦点,且经过D、E两点的椭圆与双曲线的离心率之和为________
16、已知函数y=f(x)是R上的偶函数,对于x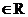 都有f(x+6)=f(x)+f(3)成立,且f(-4)=-2,当x
都有f(x+6)=f(x)+f(3)成立,且f(-4)=-2,当x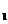 ,x
,x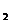
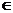 [0,3],且x
[0,3],且x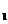
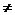 x
x 时,都有
时,都有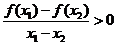 。则给出下列命题:
。则给出下列命题:
 (1)f(2008)=-2;
(1)f(2008)=-2;
(2) 函数y=f(x)图象的一条对称由为x=-6;
(3)函数y=f(x)在[-9,-6]上为减函数;
(4)方程f(x)=0在[-9,9]上有4个根;
其中所有正确命题的题号为_____
17、(本小题满分10分)
已知向量a=(cos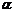 ,sin
,sin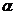 ),b=(cos
),b=(cos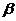 ,sin
,sin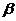 ),|a-b|=
),|a-b|=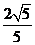 .
.
(Ⅰ)求cos(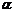 -
-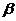 )的值
)的值
(Ⅱ)若0<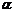 <
<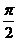 ,
,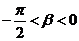 ,且sin
,且sin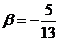 ,求sin
,求sin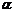 的值
的值
18、(本小题满分12分)
某体育项目的比赛规则,则三局两胜改为五局三胜的新赛制,由以往的经验,单场比赛甲胜乙的概率为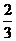 ,各局比赛相互之间没有影响。
,各局比赛相互之间没有影响。
(Ⅰ)依以往的经验,在新赛制下,求乙以3:2获胜的概率;
 (Ⅱ)试用概率知识解释新赛制对谁更有利。
(Ⅱ)试用概率知识解释新赛制对谁更有利。
19、(本小题满分12分)
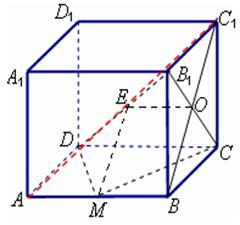
如图,在棱长为2的正方体ABCD-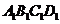 中,M为AB的中点,E为
中,M为AB的中点,E为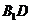 的中点,(说明:原图没有线段BC1,EO,AC1,请你自己在使用时将图修改一下)
的中点,(说明:原图没有线段BC1,EO,AC1,请你自己在使用时将图修改一下)
(Ⅰ)求证: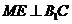 ;
;
(Ⅱ)求点M到平面DB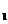 C的距离;
C的距离;
(Ⅲ)求二面角M-B1C-D的大小
20、(本小题满分12分)
在数列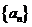 中,
中,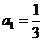 ,并且对于任意n
,并且对于任意n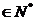 ,且
,且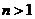 ,都有
,都有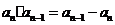 成立,令
成立,令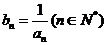
(Ⅰ)求数列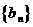 的通项公式;
的通项公式;
(Ⅱ)求数列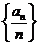 的前n项和
的前n项和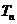 ,并证明:
,并证明: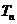 <
<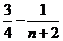 。
。
21、(本小题满分12分)
已知函数f(x)=x2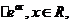 其中e为自然对数的底数,a
其中e为自然对数的底数,a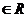
(Ⅰ)设a=-1
,x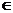 [-1,1],求函数y=f(x)的极值;
[-1,1],求函数y=f(x)的极值;
(Ⅱ)若对于任意的a>0,都有f(x)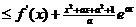 成立,求x的取值范围。
成立,求x的取值范围。
22、(本小题满分12分)
已知点A(-2,0),B(2,0),动点P满足:
(Ⅰ)求动点P的轨迹Q的方程;
(Ⅱ)过点B的直线l与轨迹Q交于两点M,N。试问x轴上是否存在定点C,使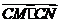 为常数,若存在,求出点C的坐标;若不存在,说明理由。
为常数,若存在,求出点C的坐标;若不存在,说明理由。
高中毕业班复习教学质量检测(二)
高中毕业班理科数学复习质量检测(二) 数学(理科)试题 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分。考试时间120分钟. 第 Ⅰ卷(选择题 共60分)参考答案
数学答案(理科)
一、选择题:本大题共12小题,每题5分,共60分.
CDDAB CACAC BB
二、填空题:本大题共4小题,每小题5分,共10分
13.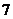 14.
14.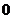 15.
15.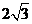 16.①②③④
16.①②③④
三、解答题:本大题共6小题,共70分.
17.(本小题满分10分)
解:(Ⅰ)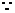
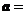 (cos
(cos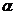 ,sin
,sin ),
), 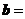 (cos
(cos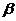 ,sin
,sin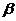 ),
),
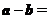 (cos
(cos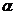 -cos
-cos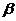 ,sin
,sin -sin
-sin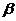 ).
).
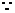
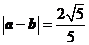 ,
,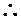
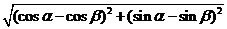 =
= ,………2分
,………2分
即2-2cos( =
=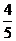 ,
,
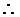 cos(
cos( =
=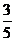 .…………………5分
.…………………5分
(Ⅱ)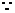 0<
0<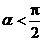 ,
,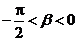 ,
,
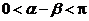 ,
,
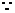 cos(
cos( =
=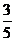 .
. sin(
sin( =
=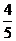 ,…………………7分
,…………………7分
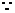 sin
sin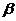 =-
=-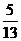 ,
, cos
cos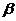 =
=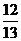 .…………………8分
.…………………8分

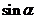 =sin
=sin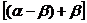 =sin(
=sin( cos
cos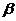 +cos(
+cos( sin
sin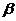
=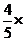
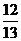 +
+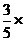 (
( )
)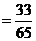 .…………………10分
.…………………10分
18.(本小题满分12分)
解:(Ⅰ)记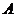 表示事件:“在新赛制下,乙以
表示事件:“在新赛制下,乙以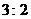 获胜”,则
获胜”,则
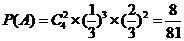 .…………………4分
.…………………4分
因此,在新赛制下,乙以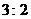 获胜的概率为
获胜的概率为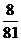 .…………………5分
.…………………5分
(Ⅱ)记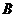 表示事件:“采用新赛制,乙获胜”,
表示事件:“采用新赛制,乙获胜”,
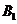 表示事件:“采用新赛制,乙以
表示事件:“采用新赛制,乙以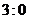 获胜”,
获胜”,
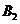 表示事件:“采用新赛制,乙以
表示事件:“采用新赛制,乙以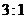 获胜”,
获胜”,
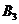 表示事件:“采用新赛制,乙以
表示事件:“采用新赛制,乙以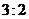 获胜”.
获胜”.
则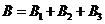 ,且
,且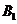 ,
,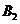 ,
,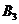 彼此互斥,
彼此互斥,
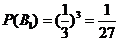 ,
,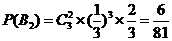 ,
,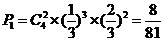 ,
,
…………………7分
采取新赛制,乙获胜的概率
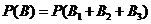
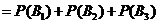
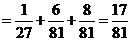 .…………………9分
.…………………9分
记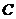 表示事件:“采取三局二胜制,乙获胜”,
表示事件:“采取三局二胜制,乙获胜”,
同理,采取三局二胜制,乙获胜的概率
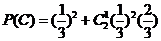 …………………10分
…………………10分
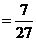
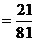
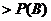 .…………………11分
.…………………11分
所以,采取新赛制对甲更有利.…………………12分
19.(本小题满分12分)
解:(Ⅰ)连接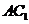 ,依题意可得
,依题意可得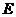 为
为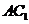 的中点,
的中点,
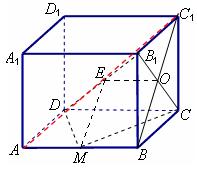 连接
连接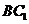 ,设
,设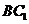 交
交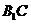 于点
于点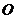 ,
,
又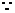
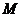 为
为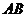 的中点,
的中点,
 ∴
∴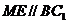 .…………2分
.…………2分
在正方形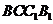 中,
中,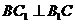 ,
,
∴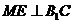 .…………………4分
.…………………4分
(Ⅱ)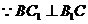 ,
,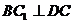 ,
,
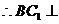 面
面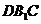 ,又
,又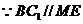 ,
,
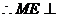 面
面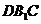 ,∴
,∴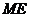 为所求距离.…………………6分
为所求距离.…………………6分
又正方体的棱长为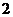 ,
, ,
,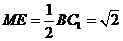 .
.
因此,点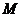 到平面
到平面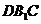 的距离为
的距离为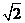 .…………………8分
.…………………8分
(也可由体积相等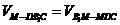 ,求得距离为
,求得距离为 )
)
(Ⅲ)连接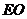 ,
,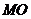 ,则
,则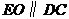 ,而
,而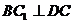 ,∴
,∴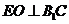 ,
,
由(Ⅱ)知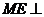 面
面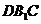 ,∴
,∴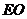 为
为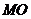 在平面
在平面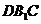 内的射影,
内的射影,
由三垂线定理知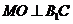 ,
,
所以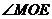 为二面角
为二面角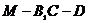 的平面角.…………………10分
的平面角.…………………10分
在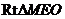 中,
中, ,
,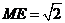 ,
,
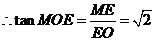 .
.
所以,二面角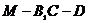 的大小为
的大小为 .…………………12分
.…………………12分
20.(本小题满分12分)
解:(I)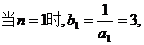 …………………1分
…………………1分
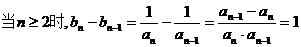 ,
…………………3分
,
…………………3分
∴数列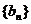 是首项为3,公差为1的等差数列, …………………4分
是首项为3,公差为1的等差数列, …………………4分
∴数列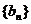 的通项公式为
的通项公式为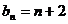 . …………………6分
. …………………6分
(II)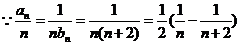 , …………………8分
, …………………8分
∴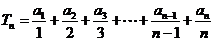

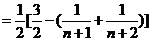
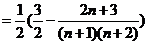 , …………………10分
, …………………10分
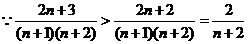 ,
,
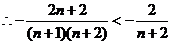 ,
,
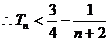 . …………………12分
. …………………12分
21.(本小题满分12分)
解:(Ⅰ)当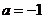 时,
时,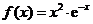 ,
,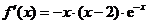 .……………2分
.……………2分
当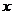 在
在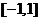 上变化时,
上变化时,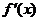 ,
,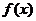 的变化情况如下表:
的变化情况如下表:
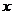 |
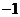 |
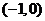 |
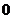 |
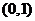 |
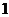 |
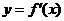 |
|
- |
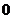 |
+ |
|
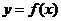 |
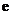 |
 |
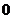 |
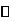 |
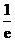 |
…………………4分
∴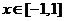 时,
时,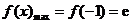 ,
,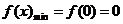 .…………6分
.…………6分
(Ⅱ)∵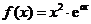 ,
,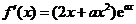 ,
,
∴原不等式等价于: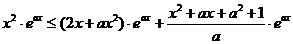 ,
,
即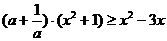 , 亦即
, 亦即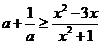 .
.
∴对于任意的 ,原不等式恒成立,等价于
,原不等式恒成立,等价于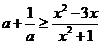 对
对 恒成立, …9分
恒成立, …9分
∵对于任意的 时,
时, 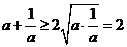 (当且仅当
(当且仅当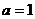 时取等号).
时取等号).
∴只需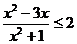 ,即
,即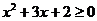 ,解之得
,解之得 或
或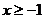 .
.
因此,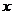 的取值范围是
的取值范围是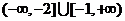 .
…………12分
.
…………12分
22.(本小题满分12分)
解: (Ⅰ)依题意,由余弦定理得: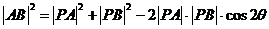 , …2分
, …2分
即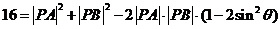
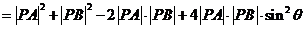
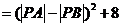 .
.
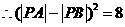 ,即
,即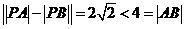 . …………4分
. …………4分
(当动点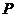 与两定点
与两定点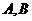 共线时也符合上述结论)
共线时也符合上述结论)
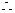 动点
动点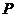 的轨迹为以
的轨迹为以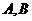 为焦点,实轴长为
为焦点,实轴长为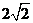 的双曲线.
的双曲线.
所以,轨迹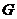 的方程为
的方程为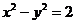 . …………6分
. …………6分
(Ⅱ)假设存在定点 ,使
,使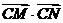 为常数.
为常数.
(1)当直线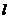 不与
不与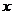 轴垂直时,
轴垂直时,
设直线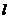 的方程为
的方程为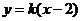 ,代入
,代入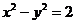 整理得:
整理得:
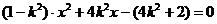 .
…………7分
.
…………7分
由题意知,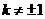 .
.
设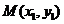 ,
,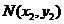 ,则
,则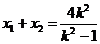 ,
,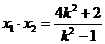 .…………8分
.…………8分
于是,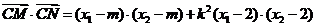 …………9分
…………9分
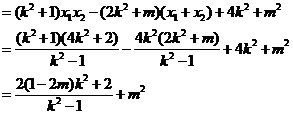
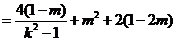 .
…………10分
.
…………10分
要使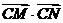 是与
是与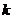 无关的常数,当且仅当
无关的常数,当且仅当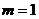 ,此时
,此时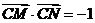 . ……11分
. ……11分
(2)当直线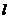 与
与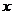 轴垂直时,可得点
轴垂直时,可得点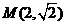 ,
,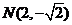 ,
,
当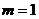 时,
时,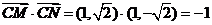 .
.
故在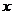 轴上存在定点
轴上存在定点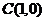 ,使
,使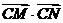 为常数.
…………12分
为常数.
…………12分