
1.已知集合M={0,1,2},N={x|x=3a,a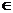 M},则集合M
M},则集合M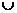 N=( )
N=( )
A.{0,1,2,3,6} B.{1,2,3,6} C.{0,3,6} D.{0}
2.函数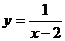 的反函数为( )
的反函数为( )
A. 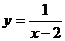 B.
B.
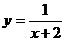 C.
C.
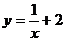 D.
D.
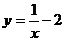
3.某校有高一学生700人,高二学生800人,高三学生600人,现学生处欲用分层抽样的方法抽取42名学生进行问卷调查,则下列判断正确的是( )
A.高一学生被抽到的概率最大 B.高三学生被抽到的概率最大
C.高三学生被抽到的概率最小 D.每名学生被抽到的概率相等
4.在各项都为正数的等比数列{an}中,首项a1=3,前三项和为21,则a3+a4+a5=( )
A.189 B.84 C.72 D.33
5.设双曲线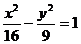 上的点P到点(5,0)的距离为15,则P点到(-5,0)的距离是( )
上的点P到点(5,0)的距离为15,则P点到(-5,0)的距离是( )
A.7 B.23 C.5或23 D.7或23
6.一个与球心距离为l的平面截球所得的圆面面积为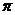 ,则球的表面积为( )
,则球的表面积为( )
A.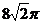 B.
B. 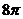 C.
C.
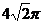 D.
D.
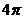
7.以P(1,1)为切点且与y=x3相切的直线方程为( )
A.3x-y-2=0 B.3x+y-4=0
C.2x-y-1=0 D.2x+y-3=0
8.若A、B为△ABC的两个内角,设命题P:△ABC为锐角三角形,命题q:sinA>cosB,则p是q的( )
A.充要条件 B.充分而不必要条件
C.必要而不充分条件 D.既不充分也不必要条件
9.已知O是△ABC所在平面内一点,满足
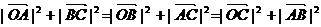 ,则点O是△ABC的( )
,则点O是△ABC的( )
A.外心 B.内心 C.垂心 D.重心
10.若x、y满足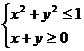 ,则2x+y的取值范围是( )
,则2x+y的取值范围是( )
A.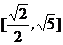 B.
B.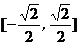 C.
C.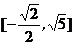 D.
D.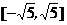
11.已知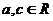 ,ac=b2,a+b+c=3.则b的取值范围是( )
,ac=b2,a+b+c=3.则b的取值范围是( )
A.[0,1] B.[-3,-1] C.(0,1] D.[-3,1]
12.某企业要从其下属6个工厂中抽调8名工程技术人员组成课题攻关小组,每厂至少调1人,则这8个名额方案共有( )
A.21种 B.15种 C.36种 D.30种
第II卷
13.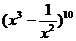 的展开式中,常数项为__________。(用数字作答)
的展开式中,常数项为__________。(用数字作答)
14.定义运算a*b=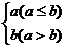 ,例如:1*2=1,则函数f(x)=sinx*cosx的值域为_________。
,例如:1*2=1,则函数f(x)=sinx*cosx的值域为_________。
15.函数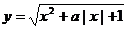 的定义域为R,则实数a的取值范围是___________。
的定义域为R,则实数a的取值范围是___________。
16.已知m、l是直线,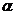 、
、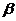 是平面,给出下列命题
是平面,给出下列命题
①若l垂直于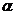 内的两条相交直线,则l⊥
内的两条相交直线,则l⊥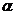 。
。
②若l平行于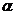 ,则l平行于
,则l平行于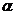 内的所有直线。
内的所有直线。
③若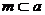 ,
,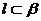 ,且l⊥m,则
,且l⊥m,则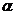 ⊥
⊥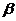
④若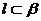 ,且l⊥
,且l⊥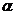 ,则
,则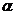 ⊥
⊥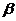
⑤若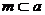 ,
,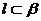 ,且
,且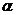 ∥
∥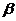 ,则m∥l。
,则m∥l。
其中正确的命题的序号是____________(注:把你认为 正确的命题的序号都填上)。
17. (本小题满分12分)
已知等差数列{an}中,公差d>0,其前n项和为Sn,且满足a2.a3=45,a1+a4=14.
(I)求数列{an}的通项公式;
(II)求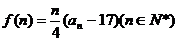 的最小值。
的最小值。
18.(本小题满分12分)
已知函数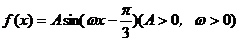 的图象经过
的图象经过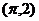 ,且其单调递增区间的最大长度为2
,且其单调递增区间的最大长度为2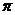 .
.
(I)求函数f(x)的解析式;
(2)若g(x)=f(x+3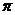 ),求g(x)的单调区间。
),求g(x)的单调区间。
19.(本小题满分12分)
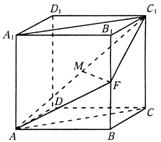
已知直四棱柱ABCD-A1B1C1D1的底面是菱形,且∠DAB=60°,AD=AA1,F为棱BB1的中点,M为线段AC1的中点。
(I)求证:直线MF∥平面ABCD;
(II)求平面AFC1与平面ABCD所成锐二面角的大小。
20.(本小题满分12分)
甲袋中有3个白球和4个黑球,乙袋中有5个白球和4个黑球,现在从甲、乙两袋中各取出2个球。
(I)求取得的4个球均是白球的概率;
(II)求取得白球个数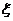 的数学期望。
的数学期望。
21.(本题满分12分)
已知命题:
P:对任意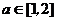 ,不等式
,不等式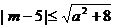 恒成立;
恒成立;
q:函数f(x)=x3+mx2+(m+6)x+1存在极大值和极小值。
求使命题“p且q”为真命题的m的取值范围。
22.(本题满分14分)
F1、F2分别双曲线x2-y2=1的两个焦点,O为坐标原点,直线l:y=kx+b与以F1F2为直径的圆相切,且直线l与双曲交于A、B两点。
(I)当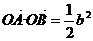 时,求直线l的方程;
时,求直线l的方程;
(II)令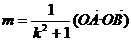 且满足2≤m≤4,求△AOB面积的取值范围。
且满足2≤m≤4,求△AOB面积的取值范围。
高中毕业班文科数学教学质量调研考试 文 科 数 学 第I卷参考答案
文科数学参考答案及评分标准
一、选择题
ACDB D BABC C DA
二、填空题
13.210 14. 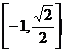 15.
15. 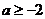 16.①④
16.①④
三、解答题
17. 解:(1)∵等差数列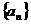 中,公差
中,公差 ,
,
∴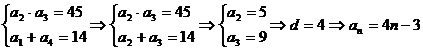 ….(6分)
….(6分)
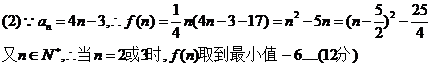
18. 解:(1)由于函数经过点(π,2),且单调递增区间的最大长度为2π,所以函数的周期是4π,………2分
因此有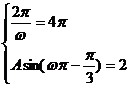 ,解得
,解得 ,………………5分
,………………5分
所以函数f
(x)的解析式是f (x)=4sin(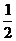 x-
x-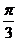 ).……………………6分
).……………………6分
(2) g(x)= f(x+3π)= 4sin(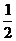 x+
x+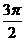 -
-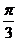 )=-4cos (
)=-4cos (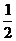 x-
x-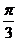 ).…………………………9分
).…………………………9分
令2kπ-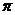 ≤
≤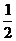 x-
x-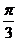 ≤2kπ,得4kπ
≤2kπ,得4kπ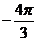 ≤x≤4kπ+
≤x≤4kπ+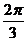 (k∈Z),所以g(x)的单调递减区间是[4kπ
(k∈Z),所以g(x)的单调递减区间是[4kπ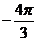 ,4kπ+
,4kπ+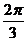 ](k∈Z).
](k∈Z).
令2kπ≤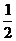 x-
x-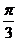 ≤2kπ+
≤2kπ+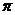 ,得4kπ+
,得4kπ+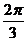 ≤x≤4kπ+
≤x≤4kπ+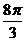 (k∈Z),所以g(x)的单调递增区间是[4kπ+
(k∈Z),所以g(x)的单调递增区间是[4kπ+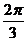 ,4kπ+
,4kπ+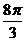 ](k∈Z).………………12分
](k∈Z).………………12分
19. 解法一:(Ⅰ)延长C1F交CB的延长线于点N,连结AN.因为F是BB1的中点,
所以F为C1N的中点,B为CN的中点. 又M是线段AC1的中点,故MF//AN.
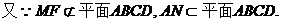
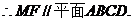 ……4分
……4分
(Ⅱ)证明:连BD,由直四棱柱ABCD-A1B1C1D1 可知: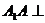 平面ABCD,
平面ABCD,
又∵BD 平面ABCD,
平面ABCD,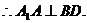
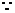 四边形ABCD为菱形,
四边形ABCD为菱形,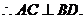
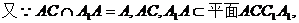

在四边形DANB中,DA∥BN且DA=BN,所以四边形DANB为平行四边形.
故NA∥BD,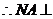 平面ACC1A1.
平面ACC1A1. 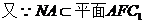
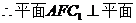 ACC1A ……8分
ACC1A ……8分
(Ⅲ)由(Ⅱ)知BD⊥ACC1A1,又AC1 ACC1A1, ∴BD⊥AC1,∵BD//NA,∴AC1⊥NA.
ACC1A1, ∴BD⊥AC1,∵BD//NA,∴AC1⊥NA.
又由BD⊥AC可知NA⊥AC, ∴∠C1AC就是平面AFC1与平面ABCD所成二面角的平面角.
在Rt△C1AC中,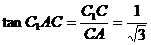 , 故∠C1AC=30°.
, 故∠C1AC=30°.
∴平面AFC1与平面ABCD所成二面角的大小为30°. ……12分
解法二:设AC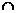 BD=O,因为M、O分别为C1A、CA的中点,所以,MO//C1C,
BD=O,因为M、O分别为C1A、CA的中点,所以,MO//C1C,
又由直四棱柱知C1C⊥平面ABCD,所以,MO⊥平面ABCD.
故可以O为原点,OB、OC、OM所在直线分别为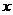 轴、
轴、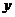 轴、
轴、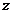 轴如图建立空间直角坐标系,若设|OB|=1,则B(1,0,0),B1(1,0,2),A(0,
轴如图建立空间直角坐标系,若设|OB|=1,则B(1,0,0),B1(1,0,2),A(0,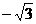 ,0),C(0,
,0),C(0,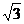 ,0),C1(0,
,0),C1(0,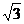 ,2).
,2).
(I)由F、M分别为B1B、C1A的中点可知:F(1,0,1),M(0,0,1), 所以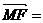 (1,0,0)=
(1,0,0)=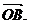
|
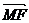 与
与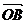 不共线,所以,MF∥OB.
不共线,所以,MF∥OB.
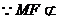 平面ABCD,OB
平面ABCD,OB 平面ABCD,
平面ABCD,
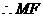 ∥平面ABCD.
…… 4分
∥平面ABCD.
…… 4分
(III)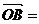 (1,0,0)为平面ACC1A1的法向量.
(1,0,0)为平面ACC1A1的法向量.
设 为平面AFC1的一个法向量,
为平面AFC1的一个法向量,
则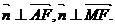 由
由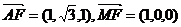 ,
,
得: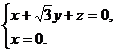 令
令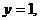 得
得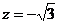 ,此时,
,此时,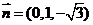 .
.
由于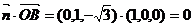 ,所以,平面AFC1⊥平面ACC1A1. …… 8分
,所以,平面AFC1⊥平面ACC1A1. …… 8分
(III)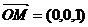 为平面ABCD的法向量,设平面AFC1与平面ABCD所成锐二面角的大小为
为平面ABCD的法向量,设平面AFC1与平面ABCD所成锐二面角的大小为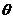 ,则
,则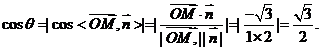 所以
所以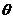 =30°
=30°
即平面AFC1与平面ABCD所成锐二面角的大小为30°.……12分
20. 解:设从甲袋中取出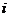 个白球的事件为
个白球的事件为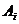 ,从乙袋中取出
,从乙袋中取出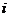 个白球的事件为
个白球的事件为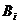 其中
其中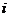 =0,1,2,则
=0,1,2,则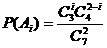 ,
,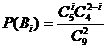 .
.
(1) 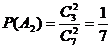 ,
,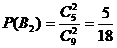 ,
,
所以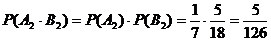 ………………………..6分
………………………..6分
(2) 至少取得三个黑球的概率,可以分两三种情况三黑一白、四黑. 则
则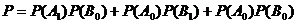
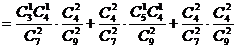
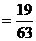 ……………………………………………………………12分
……………………………………………………………12分
21. 解: 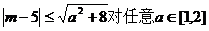 恒成立,
恒成立,
只需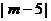 小于
小于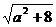 的最小值,…………………………………………2分
的最小值,…………………………………………2分
而当 时,
时,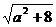 ≥3,……………………………………………4分
≥3,……………………………………………4分
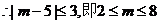 .……………………………………………………6分
.……………………………………………………6分
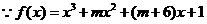 存在极大值与极小值,
存在极大值与极小值,
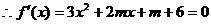 有两个不等的实根,…………………………8分
有两个不等的实根,…………………………8分
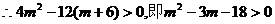 ,
,
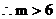 或
或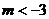 .…………………………………………………………10分
.…………………………………………………………10分
要使命题“P且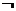 Q”为真,只需
Q”为真,只需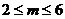 ,故m的取值范围为[2,6].…………12分
,故m的取值范围为[2,6].…………12分
22.解:(1)双曲线x2-y2=1的两个焦点分别是F1(-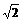 ,0),F2(
,0),F2(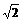 ,0),从而以F1F2为直径的圆O的方程为x2+y2=2,由于直线y=kx+b与圆O相切,所以有
,0),从而以F1F2为直径的圆O的方程为x2+y2=2,由于直线y=kx+b与圆O相切,所以有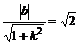
即b2=2(k2+1)(k≠±1) (2分)
设A(x1,y1),B(x2,y2),则由
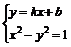 可得(k2-1)x2+2kbx+(b2+1)=0,其中k2≠1
可得(k2-1)x2+2kbx+(b2+1)=0,其中k2≠1
∴x1+x2=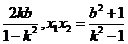
从而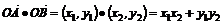
=x1x2+(kx1+b)(kx2+b)=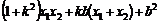
=(1+k2).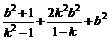
又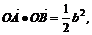 且b2=2(k2+1)
且b2=2(k2+1)
∴(1+k2).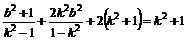
即 2k2+3-4k2+k2-1=0
∴k2=2 ∴k=±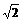 (6分)
(6分)
此时满足△=4k2b2-4(k2-1)(b2+1)>0得k2≠1
从而k=±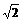 b=±
b=±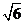
所以直线l的方程为k=±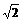 x+
x+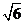 或y=±
或y=±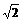 x-
x-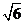
(2)类似于(1)可得m=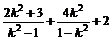
∴2k2+3-4k2+2k2-2=mk2-m
∴k2=1+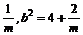
根据弦长公式
|AB|=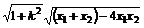
=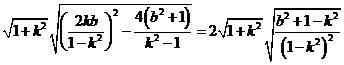
=2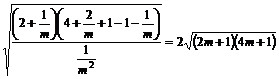
∵S△AOB=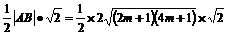
=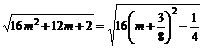 (12分)
(12分)
而2≤m≤4
∴当m=2时,△AOB的面积最小,其值为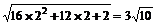
当m=4时,△AOB的面积最大,其值为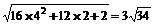
因此△AOB面积的取值范围是[3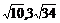 ] (14分)
] (14分)