
1.设集合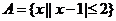 ,
,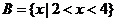 ,则
,则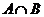 为
为
A.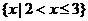 B.
B. C.
C.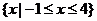 D.
D.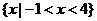
2.复数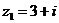 ,
,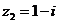 ,则
,则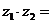
A.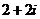 B.
B.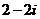 C.
C.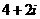 D.
D.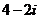
3.一个田径队,有男运动员30人,女运动员20人,比赛后,立即用分层抽样的方法,从全体队员中抽出一个容量为10的样本进行尿样兴奋剂检查,其中男运动员应抽
A.3人 B.4人 C.5人 D.6人
4.要得到函数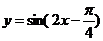 的图象,需将函数
的图象,需将函数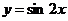 的图象
的图象
A.向左平移 个单位
B.向右平移
个单位
B.向右平移 个单位
个单位
C.向左平移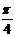 个单位
D.向右平移
个单位
D.向右平移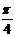 个单位
个单位
5.若随机变量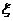 的分布列是:
的分布列是:
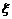 |
1 |
3 |
5 |
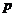 |
0.2 |
0.6 |
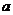 |
则其数学期望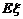 等于
等于
A.1 B.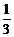 C.
C.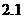 D.3
D.3
6.已知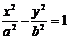 的一条渐近线方程为
的一条渐近线方程为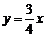 ,则双曲线的离心率为
,则双曲线的离心率为
A.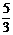 B.
B.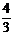 C.
C. 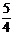 D.
D.
7.已知函数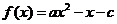 ,且
,且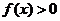 的解集为
的解集为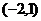 ,则函数
,则函数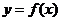 的图象大致是
的图象大致是
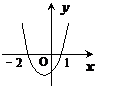
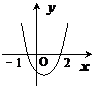
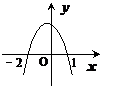
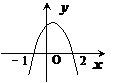
A B C D
8.设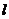 、
、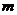 为不同的直线,
为不同的直线,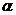 为平面,且
为平面,且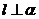 ,下列为假命题的是
,下列为假命题的是
A.若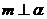 ,则
,则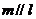 B.若
B.若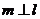 ,则
,则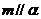
C.若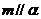 ,则
,则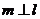 D.若
D.若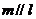 ,则
,则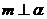
9.甲、乙、丙三位学生用计算机联网学习数学,每天上课后独立完成6道自我检测题,甲及格的概率为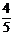 ,乙及格的概率为
,乙及格的概率为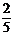 ,丙及格的概率为
,丙及格的概率为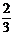 ,三人各自检测一次,则三人中至少一人及格的概率为
,三人各自检测一次,则三人中至少一人及格的概率为
A.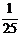 B.
B.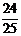 C.
C.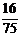 D.
D.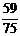
10.若把英语单词“hello”的字母顺序写错了,则可能出现的错误的种数是
A.59 B.60 C.119 D.120
11.已知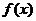 是定义在R上的不恒为零的函数,且对于任意的
是定义在R上的不恒为零的函数,且对于任意的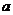 ,
,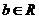 ,
,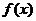 满足关系式:
满足关系式: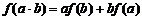 ,则
,则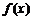 的奇偶性为
的奇偶性为
A.奇函数 B.偶函数 C.非奇非偶函数 D.既是奇函数也是偶函数
12.已知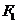 、
、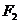 是椭圆
是椭圆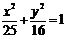 的两个焦点,P是椭圆上的一点,若
的两个焦点,P是椭圆上的一点,若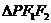 的内切圆半径为1,则点P到
的内切圆半径为1,则点P到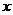 轴的距离为
轴的距离为
A. B.
B.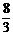 C.3
D.
C.3
D.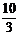
第Ⅱ卷(非选择题 共90分)
13.在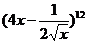 的展开式中,常数项是
(用数字作答)。
的展开式中,常数项是
(用数字作答)。
14.函数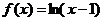 ,
,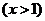 的反函数是
。
的反函数是
。
15.球面上三点A、B、C,AB=AC=BC=3,若球心到截面ABC的距离等于球半径的一半,则球的表面积为 。
16.定义运算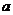 *
*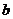 为:
为: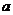 *
*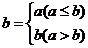 ,例如:1*2=1,则函数
,例如:1*2=1,则函数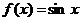 *
*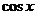 的值域为
。
的值域为
。
17.(本小题满分12分)
已知向量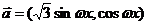 ,
,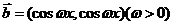 。
。
记函数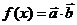 ,若函数
,若函数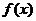 的最小正周期为
的最小正周期为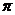 。
。
(1)求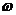 ;
;
(2)求函数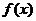 的最大值,并求此时
的最大值,并求此时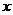 的值。
的值。
18.(本小题满分12分)
已知函数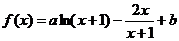 的图象与直线
的图象与直线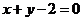 相切于点
相切于点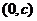 。
。
(1)求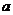 的值;
的值;
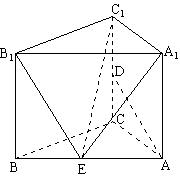 (2)求函数
(2)求函数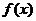 的单调区间和极小值。
的单调区间和极小值。
19.(本小题满分12分)
如图,在直三棱柱ABC-A1B1C1中, AA1=4,AB=5,BC=3,AC=4,D为CC1的中点。
(1)求异面直线AD与A1B1所成角的余弦值;
(2)试在线段AB上找一点E,使得:A1E⊥AD;
(3)求点D到平面B1C1E的距离。
20.(本小题满分12分)
某高速公路指挥部接到通知,24小时后将有一场超历史记录的大暴雨,为确保万无一失,指挥部决定在24小时内筑一道临时堤坝,以防山洪淹没正在紧张施工的隧道工程。经测算,除现有施工人员外,还须调用翻斗车搬运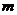 立方米的土方。已知每辆翻斗车每小时可搬运的土方量为
立方米的土方。已知每辆翻斗车每小时可搬运的土方量为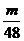 ,指挥部可调用25辆上述型号的翻斗车,但其中只有一辆可以立即投入施工,其余车辆需要从各处紧急抽调,每隔20分钟有一辆车到达并投入施工。
,指挥部可调用25辆上述型号的翻斗车,但其中只有一辆可以立即投入施工,其余车辆需要从各处紧急抽调,每隔20分钟有一辆车到达并投入施工。
(1)从第一辆车投入施工算起,第25辆车须多久才能到达?
(2)24小时内能否完成防洪堤坝工程?请说明理由。
21.(本小题满分12分)
 已知抛物线的顶点在原点,焦点F在
已知抛物线的顶点在原点,焦点F在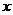 轴上。M为抛物线上的点,M的横坐标为2,且|MF|=3。
轴上。M为抛物线上的点,M的横坐标为2,且|MF|=3。
(1)求此抛物线的方程;
(2)如图,过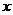 轴正半轴上任一点
轴正半轴上任一点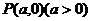 作直线与此抛物线交于A、B两点,点Q是点P关于原点的对称点。点P分有向线段
作直线与此抛物线交于A、B两点,点Q是点P关于原点的对称点。点P分有向线段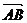 所成的比为
所成的比为 。
。
求证: 。
。
22.(本小题满分14分)
已知函数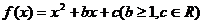 ,若
,若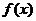 的定义域为[-1,0],值域也为
的定义域为[-1,0],值域也为
[-1,0]。
(1)求出符合条件的函数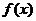 的表达式;
的表达式;
(2)若数列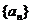 的前
的前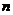 项和为
项和为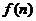 ,数列
,数列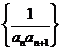 的前
的前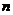 项和为
项和为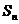 ,试求
,试求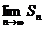 ;
;
(3)若数列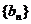 满足
满足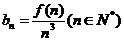 ,记数列
,记数列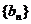 的前
的前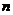 项和为
项和为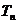 ,问是否存在正常数A,使得对于任意正整数
,问是否存在正常数A,使得对于任意正整数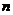 都有
都有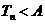 ?并证明你的结论。
?并证明你的结论。
参考解答及评分标准
1.A 2.D 3.D 4.B 5.D 6.C 7.C 8.B 9.B 10.A 11.A 12.B
13.495 14.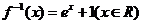 15.16
15.16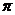 16.
16.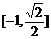
17.解:∵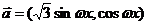 ,
,
∴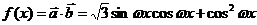 ………………………2分
………………………2分
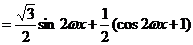 ………………………4分
………………………4分
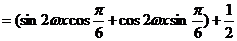
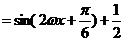 ………………………6分
………………………6分
(1)∵函数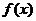 的最小正周期
的最小正周期 ,
,
∴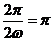 ,∴
,∴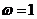 ………………………8分
………………………8分
(2)当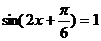 时,函数
时,函数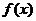 取得最大值
取得最大值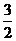 ,
,
此时,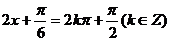 ,解得
,解得 ……………12分
……………12分
18.解:(1)∵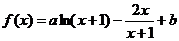 ,∴
,∴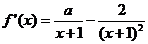 , ……2分
, ……2分
∵函数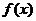 在
在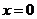 处的切线方程为
处的切线方程为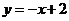 ,
,
∴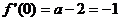 ,∴
,∴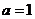 ……………………………………………………5分
……………………………………………………5分
(2)∵点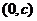 在直线
在直线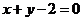 上, ∴
上, ∴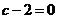 ,∴
,∴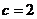 ,
,
∵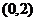 在
在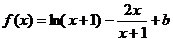 的图象上,∴
的图象上,∴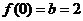 ,
,
∴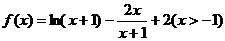 …………………………………………7分
…………………………………………7分
由(1)得: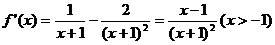 ,
,
令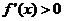 ,则
,则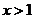 ,因此函数
,因此函数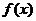 的单调递增区间为(1,+∞),……9分
的单调递增区间为(1,+∞),……9分
令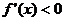 ,则
,则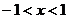 ,因此函数
,因此函数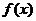 的单调递减区间为(-1,1)
的单调递减区间为(-1,1)
∴当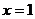 时,函数
时,函数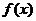 取得极小值
取得极小值 ………………………………………12分
………………………………………12分
19.解:(1)在直三棱柱ABC-A1B1C1中,
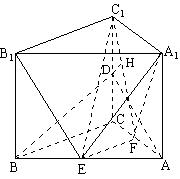 (1)∵
(1)∵ ,
,
∴ (或其补角)为异面直线AD与A1B1所成的角,
(或其补角)为异面直线AD与A1B1所成的角,
………………………2分,连结BD,
在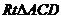 中,∵AC=4,
中,∵AC=4,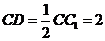
∴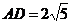 ,
,
在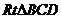 中,∵BC=3,CD=2,∴
中,∵BC=3,CD=2,∴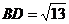 ,
,
在△ABD中,∵AB=5,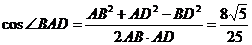
∴异面直线AD与A1B1所成角的余弦值为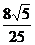 ………………………………4分
………………………………4分
(2)证明:∵AB=5,BC=3,AC=4,∴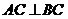 ,
,
∵底面ABC⊥侧面ACC1A1,∴BC⊥侧面ACC1A1,………………………………6分
取AB、AC的中点E、F,连结EF、A1F,则EF//BC,
∴EF⊥平面ACC1A1, ∴A1F为A1E在侧面AC1内的射影,
在正方形C1CAA1内,∵ D、F分别为CC1、AC的中点,
∴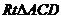 ≌
≌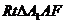 ,∴
,∴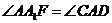 ,
,
∴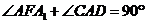 ,∴
,∴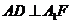 ,
,
∴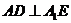 (三垂线定理)………………8分
(三垂线定理)………………8分
(3)连结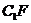 ,过D作DH⊥
,过D作DH⊥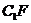 ,垂足为H。
,垂足为H。
∵EF//BC,BC//B1C1,∴EF// B1C1,∴点F在平面B1C1E内。
∵EF⊥平面ACC1A1, 平面ACC1A1,EF⊥DH,………………10分
平面ACC1A1,EF⊥DH,………………10分
∵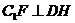 ,
,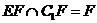 ,∴DH⊥平面B1C1E。
,∴DH⊥平面B1C1E。
在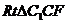 中,∵
中,∵ ,∴
,∴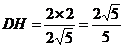 。……………12分
。……………12分
20.解:(1)设从第一辆车投入施工算起,各车到达时间依此为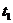 、
、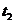 、…、
、…、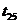 ,依题意,它们组成一个首项为0,公差为
,依题意,它们组成一个首项为0,公差为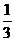 (小时)的等差数列,…………3分
(小时)的等差数列,…………3分
则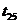 =
=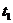 +24d,∴
+24d,∴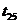 =24×
=24×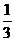 =8,
=8,
答:第25辆车须8小时后才能到达。………………6分
(2)设从第一辆车投入施工算起,各车的工作时间依次为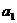 、
、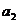 、…、
、…、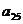 ,依题意,它们组成一个公差为-
,依题意,它们组成一个公差为-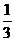 (小时)的等差数列,且
(小时)的等差数列,且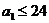 ………………8分
………………8分
∵每辆车每小时的工作效率为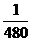 ,∴
,∴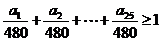
即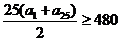 ,……………………10分
,……………………10分
又∵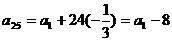 ,∴
,∴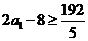 ,即
,即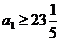 ,
,
由于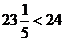 ,可见
,可见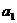 的工作时间可以满足要求,即工程可以在24小时内完成。
的工作时间可以满足要求,即工程可以在24小时内完成。
答:24小时内能完成防洪堤坝。………………………………………………12分
21.(本小题满分12分)。
(1)解:依题意,可设所求抛物线方程为: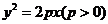
则抛物线的准线方程为: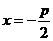 ,∴点M(2,y)到准线的距离
,∴点M(2,y)到准线的距离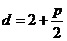 ,……2分
,……2分
由抛物线定义知: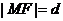 ,故
,故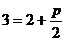 ,∴
,∴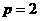 ,
,
故所求抛物线方程为: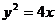 。………………4分
。………………4分
(2)证明:依题意,可设直线AB的方程为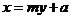 ,代入抛物线方程
,代入抛物线方程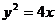 得:
得:
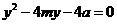 ,①
,①
设A、B两点的坐标分别是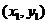 、
、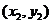 ,则
,则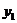 、
、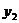 是方程①的两根,
是方程①的两根,
∵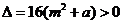 ,∴
,∴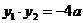 ………………6分
………………6分
由点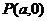 分有向线段
分有向线段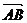 所成的比为
所成的比为 得:
得: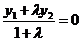 ,即
,即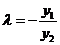 ,
,
又点Q是点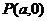 关于原点的对称点,故点Q的坐标是
关于原点的对称点,故点Q的坐标是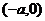 ,从而
,从而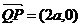 ,
,
∵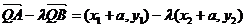
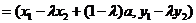 ,
,
∴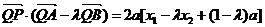 …………………………………9分
…………………………………9分
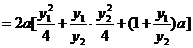
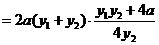
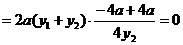 ,
,
∴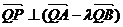 。………………………………………12分。
。………………………………………12分。
22.解:(1)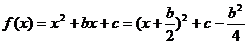 ,
,
∵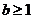 ,∴
,∴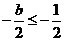 ,故当
,故当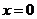 时,
时,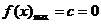 。……………………………2分
。……………………………2分
若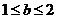 ,∴
,∴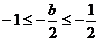 ,则
,则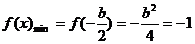 ,∴
,∴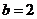
若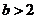 ,则
,则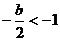 ,则
,则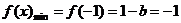 ,∴
,∴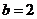 (舍去)
(舍去)
故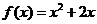 ……………………………………4分
……………………………………4分
(2)当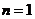 时,
时,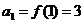 ,
,
当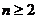 时,
时,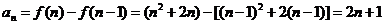
∴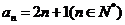 …………………………………………………6分
…………………………………………………6分
∴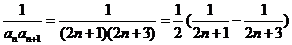 ,
,
∴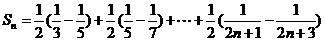
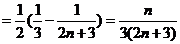
∴ ……………………………………………9分
……………………………………………9分
(3)∵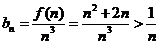 ……………………………………………10分
……………………………………………10分
∴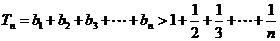 ,
,
∵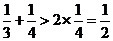 ,
,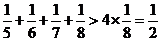 ,…………
,…………
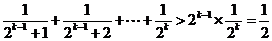 ,
,
故当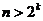 时,
时,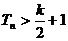 ,
,
因此,对任何常数A,设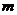 是不小于A的最小正整数,
是不小于A的最小正整数,
则当 时,必有
时,必有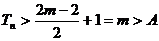 。
。
故不存在常数A使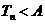 对所有
对所有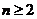 的正整数恒成立。……………………14分
的正整数恒成立。……………………14分