
1.已知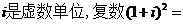
A. 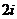 B.
B.
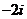 C.
C.
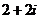 D.
D.
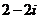
2.已知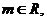 向量
向量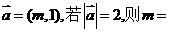
A.
1
B. 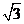 C.
C.
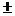 1
D.
1
D. 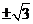
3.函数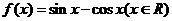 的最小正周期是
的最小正周期是
A.  B.
B.
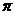 C.
C.
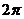 D.
D.
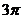
 4如图1所示,
4如图1所示,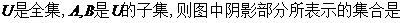
A.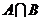 B.
B. 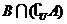
C. 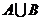 D.
D.
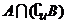
5.如果一个椭圆的长轴长是短轴长的2倍,
那么这个椭圆的离心率为
 A.
A. 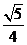 B.
B.
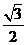
C. 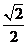 D.
D.
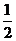
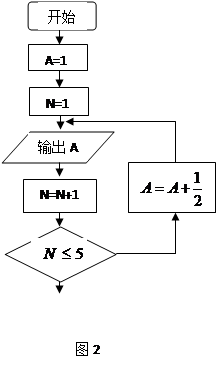
6.如图2所示的算法流程图中(注:”A=1”也可写成
”A:=1”或”A←1”,均表示赋值语句),第3个输出的数是
A.
1
B. 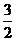
C.
2
D. 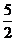
7.某市A,B.C三个区共有高中学生20000人,其中A区高中学生
|
|
|
 A. 200人
B. 205人
A. 200人
B. 205人
C. 210人 D. 215人
8下列函数中,既是偶函数又在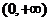 上单调递增的是
上单调递增的是
A. 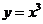 B
B
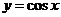 C
C 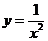 D
D
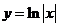
9.如果一个几何体的三视图如图2所示(单位长度:cm),
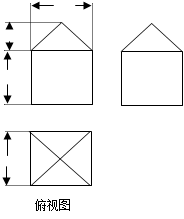 则此几何体的表面积是 4
则此几何体的表面积是 4
A. 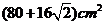 2
2
B. 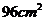 4
4
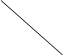
 C.
C. 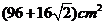 主视图 左视图
主视图 左视图
|
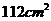 4
4
10.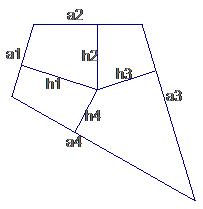 如图4所示,面积为S的平面凸四边形的第
如图4所示,面积为S的平面凸四边形的第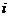 条边的边长记为
条边的边长记为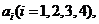 此四边形内任一点P到第
此四边形内任一点P到第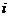 条边的距离记为
条边的距离记为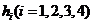 ,若
,若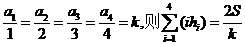 .类比以上性质,体积为V三棱锥的第
.类比以上性质,体积为V三棱锥的第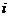 个面的面积记为
个面的面积记为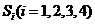 ,
,
此三棱锥内任一点Q到第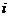 个面的距离记为
个面的距离记为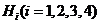 ,
,
|
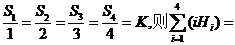
A. 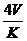 B.
B.
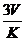
|
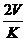 D.
D.
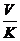
11.命题“若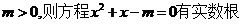 ”的逆命题是
”的逆命题是
12.双曲线的中心在坐标原点,离心率等于2,一个焦点的坐标为(2,0),则此双曲线的方程是
13.不等式组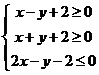 ,所确定的平面区域记为
,所确定的平面区域记为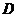 .若点
.若点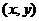 是区域
是区域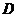 上的点,则
上的点,则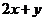 的最大值是
;若圆
的最大值是
;若圆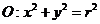 上的所有点都在区域
上的所有点都在区域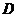 上,则圆
上,则圆 的面积的最大值是
的面积的最大值是
 ▲选做题:在下面三道小题中选做两题,三题都选的只计算前两题的得分
▲选做题:在下面三道小题中选做两题,三题都选的只计算前两题的得分
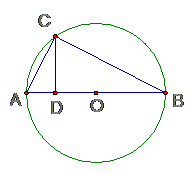
14.如图5所示, 圆 上一点C在直径AB上的射影为D,
上一点C在直径AB上的射影为D,
CD=4, BD=8, 则圆 的半径等于
的半径等于
15.在极坐标系中,圆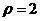 上的点到直线
上的点到直线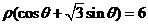
的距离的最小值是
|
16(本小题满分12分)
已知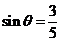
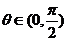 , 求
, 求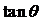
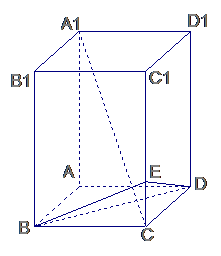 和
和 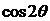 的值
的值
17.(本小题满分14分)
如图6所示,在长方体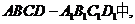
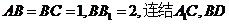
(1)求证: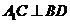
(2)求三棱锥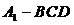 的体积
的体积
18.(本小题满分14分)
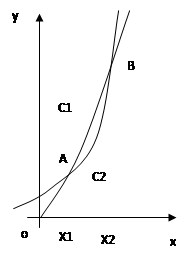 函数
函数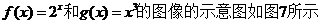
 设两函数的图像交于点
设两函数的图像交于点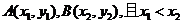
(1)请指出示意图中曲线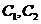 分别对应哪一个函数?
分别对应哪一个函数?
(2)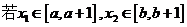 ,且
,且

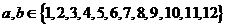 指出
指出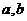 的值,并说明理由;
的值,并说明理由;
(3)结合函数图像示意图,判断

|
19.(本小题满分12分)
某工厂日生产某种产品最多不超过30件,且在生产过程中次品率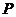 与日生产量
与日生产量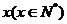
件间的关系为
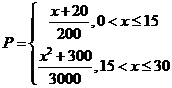
每生产一件正品盈利2900元,每出现一件次品亏损1100元.
(1)将日利润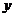 (元)表示日产量
(元)表示日产量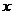 (件)的函数;
(件)的函数;
(2)该厂的日产量为多少件时,日利润最大?
(注:次品率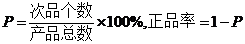 )
)
20(本小题满分14分)
已知圆C: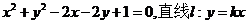 ,且
,且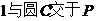 、
、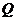 两点,点
两点,点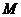
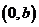 ,且
,且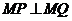 .
.
(1)当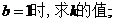
(2)当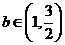 时,求
时,求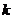 的取值范围.
的取值范围.
21(本小题满分14分)
设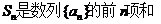 ,对任意
,对任意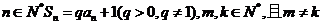
(1)求数列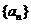 的通项公式
的通项公式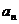
(2)试比较
(3)当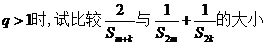
高中毕业班数学综合测试(一) 数 学(文科) 参考公式:如果事件A、B互斥,那么参考答案
数 学(文)参考答案及评分标准
一选择题(本大题共10小题,每小题5分,共50分)
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
答案 |
A |
D |
C |
B |
B |
C |
C |
D |
A |
B |
二填空题:本大题共5小题,其中11-13题是必做题,14-15题是选做题.每小题5分,满分30分,第13小题的第一空为2分,第二空3分,
11. 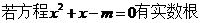 则
则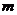 >0
>0
12.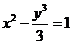
13. 14; 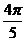
14. 5
15. 1
三、解答题:
16.本小题主要考查三角函数的诱导公式及和(差)角公式等基础知识,考查运算能力,满分12分
(1)由题意可求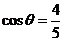 4分
4分
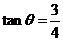 6分
6分
(2)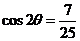 12分
12分
17.(1)略 8分
(2)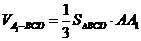 11分
11分
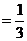 14分
14分
18.解(1) 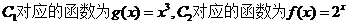 4分
4分
(2)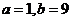 6分
6分
理由如下: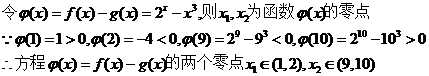
因此整数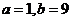 9分
9分
(3)从图像上可以看出,当 11分
11分
 13分
13分
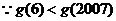
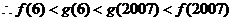 14分
14分
19解(1)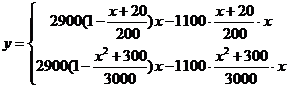
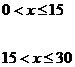
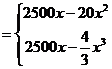
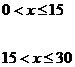 4分
4分
(2)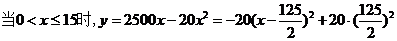
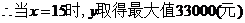 6分
6分
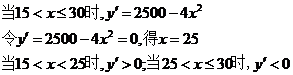
 8分
8分
 10分
10分
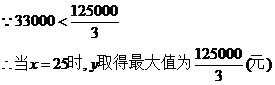
答:该厂的日产量为25件时,日利润最大. 12分
20解(1)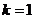 4分
4分
(2)由 消去y得
消去y得
 ①
①
设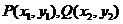 则
则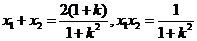 6分
6分
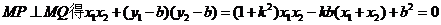 8分
8分
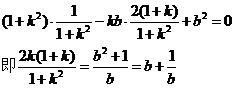
令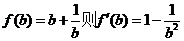
当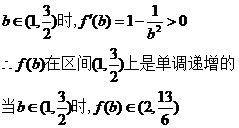 11分
11分
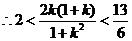 解得:
解得: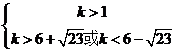
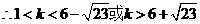 13分
13分
由①式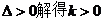
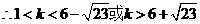
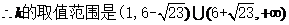 14分
14分
21解(1)当n=1时,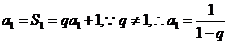 1分
1分
 3分
3分
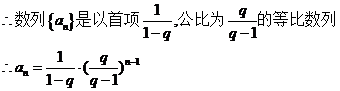 4分
4分
(2)由(1)得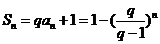 5分
5分
令
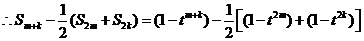 7分
7分
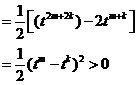
故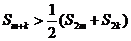 9分
9分
(3)当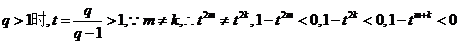

=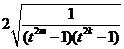 11分
11分
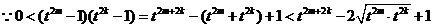

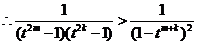 13分
13分
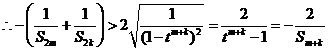
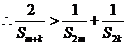 14分
14分