
1. 计算: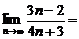 .
.
2. 方程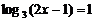 的解
的解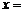 .
.
3. 函数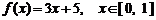 的反函数
的反函数 .
.
4. 不等式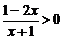 的解集是
.
的解集是
.
5. 已知圆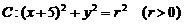 和直线
和直线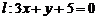 . 若圆
. 若圆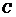 与直线
与直线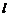 没有公共
没有公共
点,则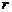 的取值范围是
.
的取值范围是
.
6. 已知函数 是定义在
是定义在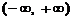 上的偶函数. 当
上的偶函数. 当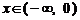 时,
时,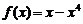 ,则
,则
当 时,
时,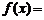 .
.
7. 电视台连续播放6个广告,其中含4个不同的商业广告和2个不同的公益广告,要求首
尾必须播放公益广告,则共有 种不同的播放方式(结果用数值表示).
8. 正四棱锥底面边长为4,侧棱长为3,则其体积为 .
9. 在△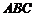 中,已知
中,已知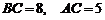 ,三角形面积为12,则
,三角形面积为12,则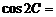 .
.
10. 若向量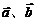 的夹角为
的夹角为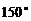 ,
,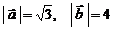 ,则
,则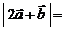 .
.
11. 已知直线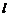 过点
过点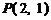 ,且与
,且与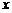 轴、
轴、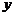 轴的正半轴分别交于
轴的正半轴分别交于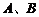 两点,
两点,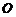 为坐标原
为坐标原
点,则三角形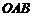 面积的最小值为 .
面积的最小值为 .
12. 同学们都知道,在一次考试后,如果按顺序去掉一些高分,那么班级的平均分将降低;
反之,如果按顺序去掉一些低分,那么班级的平均分将提高. 这两个事实可以用数学语
言描述为:若有限数列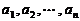 满足
满足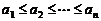 ,则
,则
(结论用数学式子表示).
13. 抛物线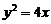 的焦点坐标为( )
的焦点坐标为( )
(A)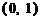 . (B)
. (B)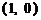 .
(C)
.
(C)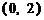 .
(D)
.
(D)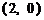 .
.
14. 若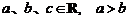 ,则下列不等式成立的是( )
,则下列不等式成立的是( )
(A)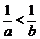 .
(B)
.
(B)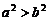 .
(C)
.
(C)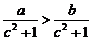 .(D)
.(D)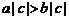 .
.
15. 若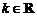 ,则“
,则“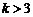 ”是“方程
”是“方程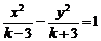 表示双曲线”的( )
表示双曲线”的( )
(A)充分不必要条件. (B)必要不充分条件.
(C)充要条件. (D)既不充分也不必要条件.
16. 若集合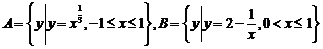 ,则A∩B等于( )
,则A∩B等于( )
(A)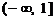 . (B)
. (B)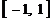 .
(C)
.
(C)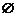 .
(D)
.
(D)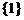 .
.
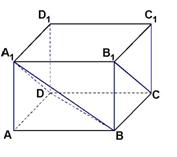
17. (本题满分12分)在长方体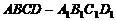 中,已知
中,已知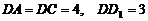 ,求异面直线
,求异面直线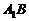 与
与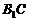 所成角的大小(结果用反三角函数值表示).
所成角的大小(结果用反三角函数值表示).
18. (本题满分12分) 已知复数 满足
满足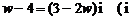 为虚数单位),
为虚数单位),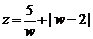 ,求一个以
,求一个以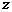 为根的实系数一元二次方程.
为根的实系数一元二次方程.
19. (本题满分14分) 本题共有2个小题,第1小题满分8分,第2小题满分6分.
已知函数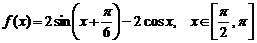 .
.
(1)若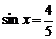 ,求函数
,求函数 的值; (2)求函数
的值; (2)求函数 的值域.
的值域.
20. (本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
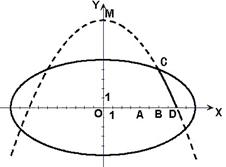
学校科技小组在计算机上模拟航天器变轨返回试验. 设计方案如图:航天器运行(按顺时针方向)的轨迹方程为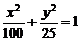 ,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以
,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以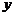 轴为对称轴、
轴为对称轴、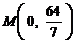 为顶点的抛物线的实线部分,降落点为
为顶点的抛物线的实线部分,降落点为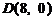 . 观测点
. 观测点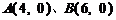 同时跟踪航天器.
同时跟踪航天器.
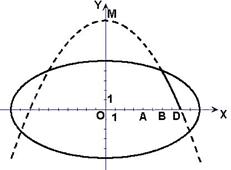 (1)求航天器变轨后的运行轨迹所在的曲线方程;
(1)求航天器变轨后的运行轨迹所在的曲线方程;
(2)试问:当航天器在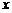 轴上方时,观测点
轴上方时,观测点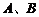 测得离航天器的距离分别为多少时,应向航天器发出变轨指令?
测得离航天器的距离分别为多少时,应向航天器发出变轨指令?
21. (本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
设函数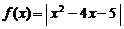 .
.
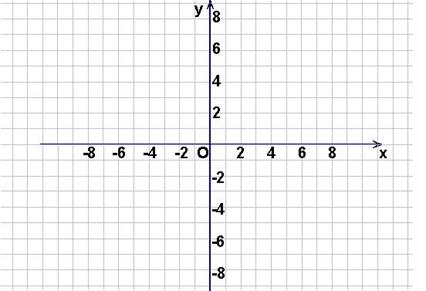
(1)在区间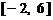 上画出函数
上画出函数 的图像;
的图像;
(2)设集合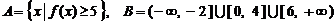 . 试判断集合
. 试判断集合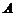 和
和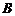 之间的关系,并给出证明;
之间的关系,并给出证明;
(3)当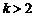 时,求证:在区间
时,求证:在区间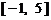 上,
上,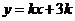 的图像位于函数
的图像位于函数 图像的上方.
图像的上方.
22. (本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分8分. 第3小题满分6分.
已知数列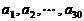 ,其中
,其中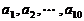 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列;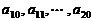 是公差为
是公差为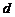 的等差数列;
的等差数列;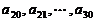 是公差为
是公差为 的等差数列(
的等差数列(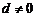 ).
).
(1)若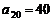 ,求
,求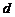 ;
;
(2)试写出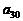 关于
关于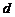 的关系式,并求
的关系式,并求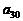 的取值范围;
的取值范围;
(3)续写已知数列,使得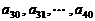 是公差为
是公差为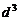 的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
高中毕业春季招生考试数学卷
高中毕业春季招生考试数学卷 数 学 试 卷参考答案
数 学 试 卷
参考答案及评分标准
一.(第1至12题)每一题正确的给4分,否则一律得零分.
1. 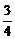 .
2. 2. 3.
.
2. 2. 3. 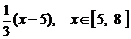 . 4.
. 4. 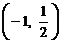 .
.
5. 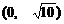 . 6.
. 6.
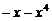 . 7. 48. 8.
. 7. 48. 8. 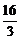 .
.
9. 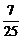 . 10.
2. 11. 4.
. 10.
2. 11. 4.
12. 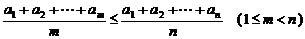 和
和
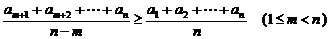
二.(第13至16题)每一题正确的给4分,否则一律得零分.
|
题 号 |
13 |
14 |
15 |
16 |
|
代 号 |
B |
C |
A |
B |
三.(第17至22题)
17. [解法一] 连接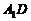 ,
,
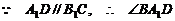 为异面直线
为异面直线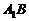 与
与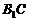 所成的角. ……4分
所成的角. ……4分
连接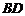 ,在△
,在△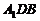 中,
中,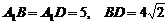 ,
……6分
,
……6分
 则
则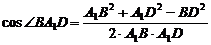
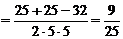 . ……10分
. ……10分
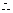 异面直线
异面直线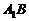 与
与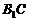 所成角的大小为
所成角的大小为 .
……12分
.
……12分
[解法二] 以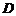 为坐标原点,分别以
为坐标原点,分别以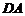 、
、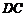 、
、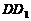 所在直线为
所在直线为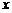 轴、
轴、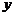 轴、
轴、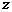 轴,建立空间直角坐标系.
……2分
轴,建立空间直角坐标系.
……2分
则 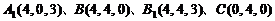 ,
,
 得
得 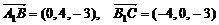 .
……6分
.
……6分
设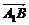 与
与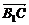 的夹角为
的夹角为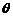 ,
,
则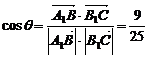 , ……10分
, ……10分
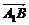 与
与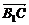 的夹角大小为
的夹角大小为 ,
,
即异面直线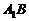 与
与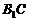 所成角的大小为
所成角的大小为 .
……12分
.
……12分
18. [解法一] 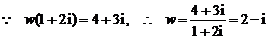 ,
……4分
,
……4分
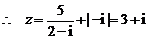 .
……8分
.
……8分
若实系数一元二次方程有虚根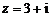 ,则必有共轭虚根
,则必有共轭虚根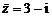 .
.
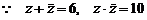 ,
,
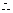 所求的一个一元二次方程可以是
所求的一个一元二次方程可以是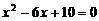 .
……12分
.
……12分
[解法二] 设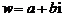
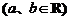
 ,
,
得 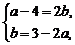
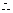
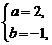
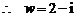 ,
……4分
,
……4分
以下解法同[解法一].
19. [解](1)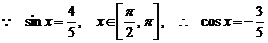 ,
……2分
,
……2分
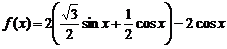 ……4分
……4分
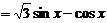
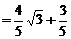 .
……8分
.
……8分
(2)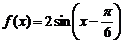 ,
……10分
,
……10分
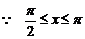 ,
, 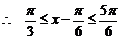 ,
,  ,
,
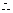 函数
函数 的值域为
的值域为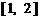 .
……14分
.
……14分
20. [解](1)设曲线方程为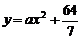 , 由题意可知,
, 由题意可知,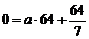 .
.
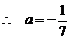 . ……4分
. ……4分
 曲线方程为
曲线方程为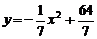 .
……6分
.
……6分
 (2)设变轨点为
(2)设变轨点为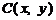 ,根据题意可知
,根据题意可知
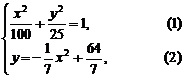 得
得 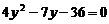 ,
,
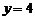 或
或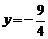 (不合题意,舍去).
(不合题意,舍去).
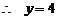 .
……9分
.
……9分
得 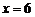 或
或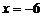 (不合题意,舍去).
(不合题意,舍去). 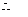
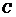 点的坐标为
点的坐标为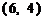 ,
……11分
,
……11分
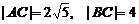 .
.
答:当观测点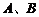 测得
测得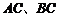 距离分别为
距离分别为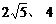 时,应向航天器发出变轨指令.
……14分
时,应向航天器发出变轨指令.
……14分
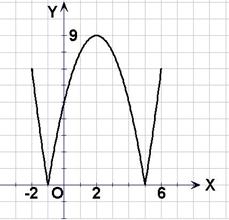 21. [解](1)
21. [解](1)
……4分
(2)方程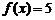 的解分别是
的解分别是 和
和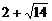 ,由于
,由于 在
在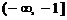 和
和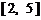 上单调递减,在
上单调递减,在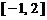 和
和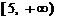 上单调递增,因此
上单调递增,因此
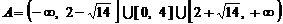 .
……8分
.
……8分
由于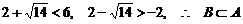 .
……10分
.
……10分
(3)[解法一] 当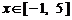 时,
时,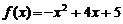 .
.
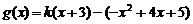
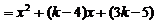
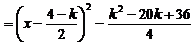 ,
……12分
,
……12分
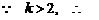
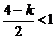 . 又
. 又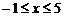 ,
,
① 当 ,即
,即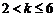 时,取
时,取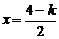 ,
,
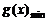
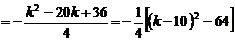 .
.
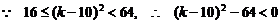 ,
,
则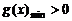 .
……14分
.
……14分
② 当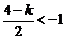 ,即
,即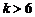 时,取
时,取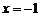 ,
, 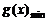 =
=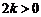 .
.
由 ①、②可知,当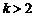 时,
时,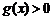 ,
,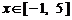 .
.
因此,在区间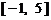 上,
上,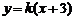 的图像位于函数
的图像位于函数 图像的上方. ……16分
图像的上方. ……16分
[解法二] 当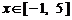 时,
时,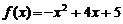 .
.
由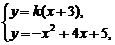 得
得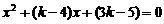 ,
,
令 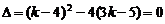 ,解得
,解得
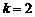 或
或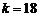 ,
……12分
,
……12分
在区间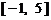 上,当
上,当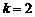 时,
时,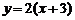 的图像与函数
的图像与函数 的图像只交于一点
的图像只交于一点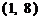 ; 当
; 当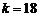 时,
时,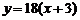 的图像与函数
的图像与函数 的图像没有交点. ……14分
的图像没有交点. ……14分
如图可知,由于直线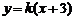 过点
过点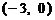 ,当
,当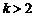 时,直线
时,直线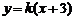 是由直线
是由直线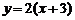 绕点
绕点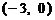 逆时针方向旋转得到. 因此,在区间
逆时针方向旋转得到. 因此,在区间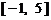 上,
上,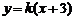 的图像位于函数
的图像位于函数 图像的上方.
……16分
图像的上方.
……16分
22. [解](1)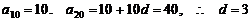 .
…… 4分
.
…… 4分
(2)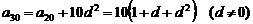 ,
…… 8分
,
…… 8分
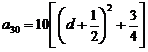 ,
,
当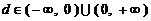 时,
时,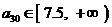 .
…… 12分
.
…… 12分
(3)所给数列可推广为无穷数列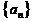 ,其中
,其中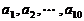 是首项为1,公差为1的等差数列,当
是首项为1,公差为1的等差数列,当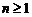 时,数列
时,数列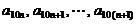 是公差为
是公差为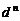 的等差数列.
…… 14分
的等差数列.
…… 14分
研究的问题可以是:试写出 关于
关于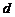 的关系式,并求
的关系式,并求 的取值范围.…… 16分
的取值范围.…… 16分
研究的结论可以是:由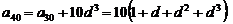 ,
,
依次类推可得 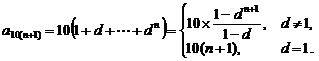
当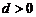 时,
时,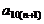 的取值范围为
的取值范围为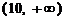 等.
…… 18分
等.
…… 18分