
1. 由等式x4 + a1x3
+ a2x2 + a3x + a4
= ( x + 1 )4 + b1 ( x + 1 )3
+ b2 ( x + 1 )2 + b3 ( x
+ 1 ) + b4,定义映射f : ( a1, a2,
a, a4 ) → ( b1 ,b2, b3
,b4 ),则f ( 4, 3, 2 ) = ( )
由等式x4 + a1x3
+ a2x2 + a3x + a4
= ( x + 1 )4 + b1 ( x + 1 )3
+ b2 ( x + 1 )2 + b3 ( x
+ 1 ) + b4,定义映射f : ( a1, a2,
a, a4 ) → ( b1 ,b2, b3
,b4 ),则f ( 4, 3, 2 ) = ( )
A.(1,2,3,4) B.(0,3,4,0)
C.(–1,0,2,–2) D.(0,–3,4,–1)
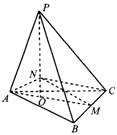
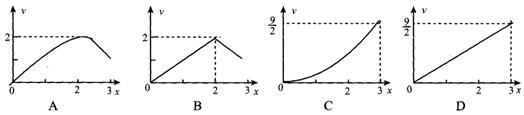
2.如图,三棱锥P-ABC的高PO = 8,AC = BC = 3,∠ACB = 30°,M、N分别在BC和PO上,且CM = x,PN = 2 cm,则下面四个图象中大致描绘了三棱锥N -AMC的体积V与x ( x∈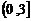 )的变化关系的是( )
)的变化关系的是( )
3.定义在实数集上的偶函数f ( x ),满足f ( x + 2 ) = f ( x ),且f ( x )在[ –3 ,–2
]上单调递减,又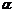 、
、 是锐角三角形的三个内角,则( )
是锐角三角形的三个内角,则( )
A.f ( sin 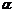 )>f ( sin
)>f ( sin  ) B.f ( cos
) B.f ( cos 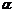 )<f ( cos
)<f ( cos  )
)
C.f ( sin 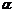 )>f ( cos
)>f ( cos  ) D.f ( sin
) D.f ( sin 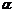 ) <f ( cos
) <f ( cos  )
)
4.已知P是以F1、F2为焦点的椭圆
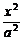 +
+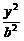 =1 ( a>b>0 )上一点,若
=1 ( a>b>0 )上一点,若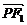 .
.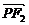 = 0,tan∠PF1F2 =
= 0,tan∠PF1F2 =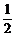 ,则此椭圆的离率为( )
,则此椭圆的离率为( )
A.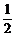 B.
B.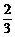 C.
C. D.
D.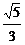
5.(理)甲、乙、丙投篮一次命中的概率分别为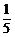 、
、 、
、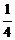 ,现三人各投篮一次至少有1人命中的概率为( )
,现三人各投篮一次至少有1人命中的概率为( )
A.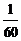 B.
B.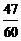 C.
C.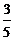 D.
D.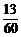
(文)5人随意排一排,如果甲不在左端,乙不在右端的概率是( )
A.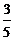 B.
B. C.
C.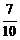 D.
D.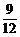
6.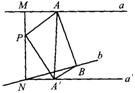 设MN为互相帮助垂直的异面直线a、b的公垂线,P为MN上不同于M、N的点,A、B分别为a、b上的点,则三角形APB为( )
设MN为互相帮助垂直的异面直线a、b的公垂线,P为MN上不同于M、N的点,A、B分别为a、b上的点,则三角形APB为( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.都有可能三角形
7.(理)设f ( x )、g ( x )在[ a , b ]上可导,且f′( x )>g′( x ),则当a<x<b时,有( )
A.f ( x )>g ( x ) B.f ( x )<g ( x )
C.f ( x ) + g ( x )>g ( x ) + f ( a ) D.f ( x ) + g ( b )>g ( x ) + f ( b )
(文)曲线y = x3在点P处的切线斜率为k,当k = 3时的P点坐标为( )
A.(–2,–8) B.(–1,–1)或(1,1)
C.(2,8) D.(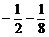 )
)
8.将函数y =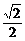 (
cos 3x – sin 3x )的图象沿向量a = ( h , 0 )平移,可以得到y = – sin 3x的图象,其中h = ( )
(
cos 3x – sin 3x )的图象沿向量a = ( h , 0 )平移,可以得到y = – sin 3x的图象,其中h = ( )
A.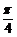 B.
B.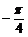 C.
C.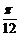 D.
D.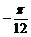
|
|
|
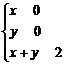 确定的平面区域内,则点N ( a + b , a – b )所在平面区域的面积是( )
确定的平面区域内,则点N ( a + b , a – b )所在平面区域的面积是( )
A.1 B.2 C.4 D.8
10.给出四个函数,分别满足
①f ( x + y ) = f ( x ) + f ( y ) ②g ( x + y ) = g ( x ).g ( y )
③h ( x.y ) = h ( x ) + h ( y ) ④t ( x.y ) = t ( x ) + t ( y )
又给出四个函数图象
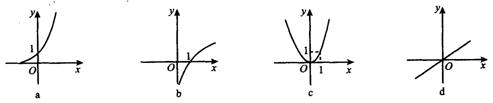 正确的匹配方案是( )
正确的匹配方案是( )
A.①-a,②-b,③-c,④-d B.①-b,②-c,③-a,④-d
C.①-c,②-a,③-b,④-d D.①-d,②-a,③-b,④-c
11.设{an}是等差数列,从{a1 , a2 ,…, a20}中任取3个不同的数,使这3个数仍成等差数列,则这样不同的等差数列最多有( )
A.90个 B.120个 C.180个 D.200个
12.已知f ( x ) = 3x–b ( 2≤x≤4 ,b为常数)的图象经过(2,1),则F (x ) = [f–1( x ) ]2 – f–1 ( x )2的值域为( )
A.[2,5] B.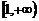 C.[2,10] D.[2,13]
C.[2,10] D.[2,13]
第Ⅱ卷(非选择题 共90分)
13.若函数f ( x )对任意实数x满足f ( x + 2 ) =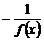 , 且f ( 1 ) = –5, 则f [f ( 5 )] =______。
, 且f ( 1 ) = –5, 则f [f ( 5 )] =______。
14.f ( x ) sin4x –2sinx.cosx + cos4x , 则函数f ( x )的值域是_____________。
15.(理)某新品的次品率为5%,今在这产品中抽查200件, 表示抽到的次品数,则E
表示抽到的次品数,则E =__________
。
=__________
。
(文)某校一年级有甲、乙两班,甲班有40人,乙班有50人。一次考试中,甲班的平均成绩是90分,乙班的平均成绩是不是81分,则该校一年级的平均成绩是____________。
16.不等式| x –3 | + | y + 3 | ≤2围成的图形的面积是_____________。
17.(本小题满分12分)
解关于x的不等式: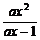 >x 。
>x 。
18.(本小题满分12分)
波士顿 ( boston )的水位午夜12点是高潮位,水面高出海平面3.01 m,早晨低潮位,水面高出海平面0.01 m ;水位的变化呈周期性变化,试选择一个函数,描述水位的变化。
(1)写出函数的解析式;
(2)求出午后两点的水位。
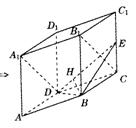
19.如图所示,已知直平行六面体ABCD-A1B1C1D1中AD⊥BD,AD = BD = a , E是CC1的中点,A1D⊥BE。
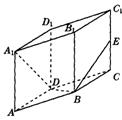 (1)求证:A1D⊥平面BDE ;
(1)求证:A1D⊥平面BDE ;
(2)求二面角E-BD-C的大小;
(3)求点B到平面A1DE的距离。
20.(本小题满分12分)
数列{an}的前n项和记为Sn,已知a1 = 1 , an+1
=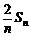 ( n≥1)
( n≥1)
(1)求数列{an}的通项公式;
(2)设bn = 2n.an ,求{bn}的前n项和Tn 。
21.(本小题满分12分)
(理)已知函数f ( x ) = x2 + alnx + 1 , ( a≠0 ) 。
(1)若f ( x )在区间 ( 0 , 2 )上是减函数,求实数a的取值范围;
(2)函数y = f ( x )的图像上是否存在两条与直线y = 2x 平行或重合的切线,若存在,求出a的范围;若不存在,说明理由。
(文)已知a为实数,函数f ( x ) = (x2 –4 )( x – a ).
(1)若函数y = f ( x ) 在 ( 0 , 2 )上是减函数a的取值范围;
(2)是否存在a的值,使y = f ( x )的切线与y = – 5x平行,若存在,求出a的值,若不存在,说明理由。
22.(本小题满分14分)
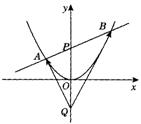
如图所示,过抛物线x2 = 4y的对称轴上任一点P ( 0 , m ) ( m>0 )作直线抛物线交于A、B两点,点Q是点P关于原点的对称点。
(1)设点P分有向线段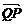 ⊥(
⊥(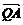 –
–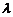
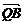 );
);
(2)设直线AB的方程是x – 2y + 12 = 0 , 过A、B两点的圆C与抛物线在点A处有共同的切线,求圆C的方程。
高考数学难点互动达标提高测试卷 数学(文理合卷) 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。满分150分。考试时间120分钟。 第Ⅰ卷(选择题 共60分) 参考答案
参考答案
1.D 2.A 3.C 4.D 5.(理)C (文)B 6.B 7.(理)C
(文)B 8.D 9.C 10.D 11.C 12.A
13.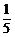
14.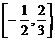
15.(理)10 (文)85
16.8
17.解:把原不等式变为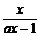 >0 ,(3分)
>0 ,(3分)
∴当a = 0 ,原不等式的解集为(-∞,0) (6分)
a>0时,原不等式的解集为(-∞,0)∪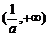 (9分)
(9分)
当a<0时,原不等式的解集为(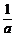 ,0)(12分)
,0)(12分)
18.解:(1)易选择y = A cos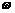 t + B的解析式(2分)
t + B的解析式(2分)
进而求A = 1.5 , 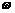 =
=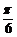 , B
= 1.51。所以函数解析式为:
, B
= 1.51。所以函数解析式为:
y
= 1.5 cos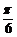 t +1.51 。(8分)
t +1.51 。(8分)
(2)由(1)可知当t = 14时,
y = 1.5 cos (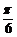 ×14 ) + 1.51 = 1.5×
×14 ) + 1.51 = 1.5×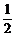 +
1.51 = 2.26 (m)
+
1.51 = 2.26 (m)
所以,午后两点水位高出海平面2.26 m (12分)
 19.(1)
19.(1)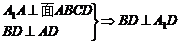 ,
,
又A1D⊥BE,所以A1D⊥面BDE 。(4分)
(2)连接如图所示B1C ,
|
|
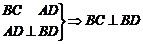
EC⊥面ABCD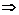 EC⊥BD
EC⊥BD
为二面角E-BD-C的平面角。由△BB1C∽△CBE
可得EC =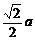 ,
,
所以tan∠EBC =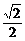 ,∠EBC = arctan
,∠EBC = arctan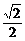 (8分)
(8分)
(3)连接DE,作HB垂直DF于H,则易证BH⊥面DA1E,BH的长即为所求。在直角三角形BDE中,易求得BH =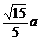 。也可用VB–A1DE = VE
–A1DB 求解。(12分)
。也可用VB–A1DE = VE
–A1DB 求解。(12分)
20.解:(1)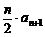 = Sn ,( n≥1)
= Sn ,( n≥1) 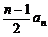 = Sn–1 (
n≥1 )
= Sn–1 (
n≥1 )
∴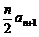 –
–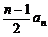 = an , ( n≥2 ) 。(4分)
= an , ( n≥2 ) 。(4分)
整理得:an+1 =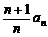 ,(n≥2) ,
,(n≥2) ,
an
= 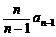 , (3分)
, (3分)
an–1
=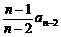
…
a3
=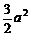
各式相乘得:an =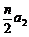 (n≥3)
(n≥3)
由已知可得a2 = 2 , a1 = 1 , 所以an = n , ( n ≥1) (6分)
(2)bn = 2n .n,由错位相减法可得Tn = ( n – 1 ).2n+1 + 2 (12分)
21.解:(理)f′( x
) = 2x + 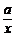 ,
,
(1)由题意有f′( x )≤0在x∈(0,2)上恒成立。
所以当x∈(0,2)时,2x +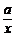 ≤0恒成立。
≤0恒成立。
即:x∈(0,2)时,a≤– 2x2∈(-∞,0)
所以a≤– 8(6分)
(2)假设存在与y = 2x平行或重合的切线,则2x +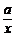 = 2有正根。
= 2有正根。
即:方程a = – 2x2 + 2x = –2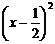 +
+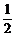 有正数解。(8分)
有正数解。(8分)
当a>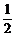 时,不存在满足条件的切线;
时,不存在满足条件的切线;
当a =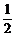 时,存在一条满足条件的切线;
时,存在一条满足条件的切线;
当0<a<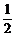 时,存在两条满足条件的切线;
时,存在两条满足条件的切线;
当a<0时,存在一条满足条件的切线。(12分)
(文)f′( x ) = 3x2 – 2ax – 4 ,
(1)由题意:f′( x )≤0在x∈(0,2)上恒成立。
|
|
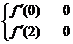 解之得a≥2 (6分)
解之得a≥2 (6分)
(2)假设存在满足条件的a的值,则关于x的一元二次方程
3x2 – 2ax – 4 = –5 有解,即△= 4a2 –12≥0成立,
所以a≥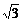 或a≤
或a≤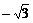 。(12分)
。(12分)
22.解:(1)依题意,可设直线AB的方程为y = kx + m ,代入抛物线方程x2 = 4y得
x2 – 4kx – 4m – 0 ① (2分)
设A,B两点的坐标分别是( x1,y1 ) , ( x2,y2 ),则x1, x2是方程①的两根,所以x1x2 = – 4 m,由点P ( 0 , m ) 分有向线段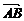 所成的比为
所成的比为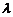 ,得
,得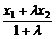 = 0,即
= 0,即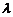 = –
= –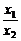 ,又点Q是点P关于原点的对称点,故点Q的坐标是 ( 0 , m ) ,从而
,又点Q是点P关于原点的对称点,故点Q的坐标是 ( 0 , m ) ,从而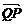 = ( 0, 2m )。
= ( 0, 2m )。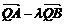 = (
x1 , y1 + m ) –
= (
x1 , y1 + m ) –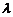 ( x2 , y2
+ m ) = ( x1 –
( x2 , y2
+ m ) = ( x1 –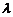 x2
, y1 + ( 1 –
x2
, y1 + ( 1 –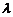 ) m ) 。
) m ) 。
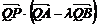 = 2m [y1
–
= 2m [y1
–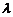 y2 + ( 1 –
y2 + ( 1 –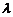 ) m ]
) m ]
= 2m
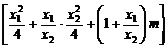
=2m
( x1 + x2 ).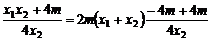 = 0
= 0
所以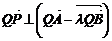 。(7分)
。(7分)
(2)由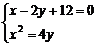 得点A、B的坐标分别是(–4 ,4)和(6,9)
得点A、B的坐标分别是(–4 ,4)和(6,9)
由x2 = 4y得y = 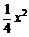 ,
,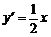 所以折射线x2 = 4y在点A处切线的斜率为y′| x = –
4 = –2 (9分)
所以折射线x2 = 4y在点A处切线的斜率为y′| x = –
4 = –2 (9分)
设圆C的方程是(x – a )2 + ( y – b )2 = r2
则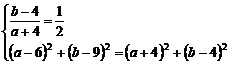
解之得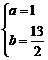
r2
= ( a + 4 )2 + ( b – 4 )2 =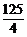
所以圆C的方程是( x –1 )2
+ 
即x2 + y2 –2x –13y + 12 = 0 (14分)