
例1.如图,在四棱锥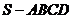 中,
中,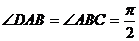 ,
,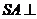 平面
平面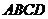 ,
,
且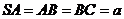 ,
,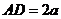 ,求点
,求点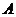 到平面
到平面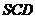 的距离.
的距离.
解:取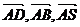 的方向分别为
的方向分别为
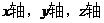 的正方向,建立空间直角坐标系,
的正方向,建立空间直角坐标系,
则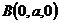 ,
,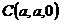 ,
,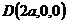

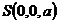 .
.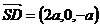 ,
,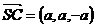
设平面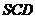 的法向量为
的法向量为
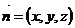 ,
,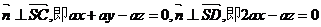 .所以可令
.所以可令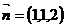 ,点
,点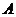 到
到
平面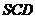 的距离
的距离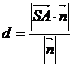 =
=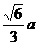 .
.
 例2.如图,已知
例2.如图,已知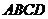 是正方形,
是正方形,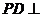 平面
平面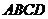 ,
,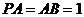 ,
,
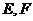 分别是
分别是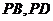 的中点,求异面直线
的中点,求异面直线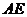 与
与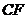 之间的距离。
之间的距离。
 解:以
解:以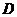 为原点,建立空间直角坐标系,
为原点,建立空间直角坐标系,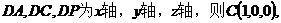
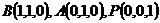
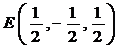 ,
,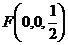 ,
,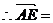
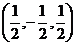 ,
,
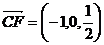 ,
,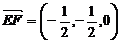 ,
,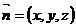 是异面直线
是异面直线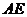 与
与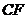 的公共法向量,则
的公共法向量,则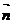
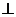
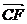 即
即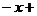
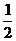
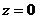 ;
;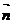
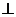
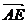 即
即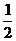
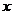
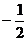
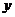 +
+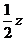 =0.所以
=0.所以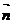 =
=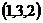 ,所以异面直线
,所以异面直线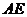 与
与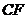 之间的距离
之间的距离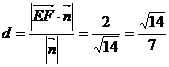 .
.
例3.如图,在直三棱柱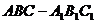 中,底面是等腰直角三角形,
中,底面是等腰直角三角形,
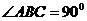 .侧棱
.侧棱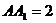 ,
,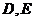 分别是
分别是 与
与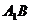 的中点,点
的中点,点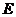 在平面
在平面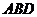 上的射影是
上的射影是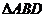 的重心
的重心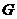 .
.
 求
求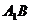 与平面
与平面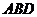 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);
 求点
求点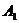 到平面
到平面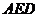 的距离.
的距离.
(1)建立如图坐标系,设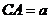 ,则
,则

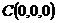 ,
,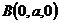 ,
,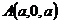 ,
,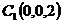 ,
,
 ,
,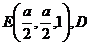
 ,
,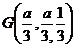 则
则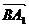 =
=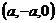 ,
,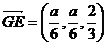
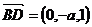 ,
,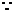
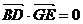
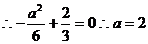 ,则
,则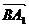 =
=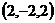 ,
,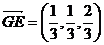 ,取平面
,取平面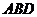 法向量为
法向量为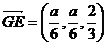 ,则
,则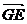 与
与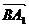 夹角为
夹角为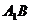 与平面
与平面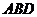 所成角的余角.所以cos
所成角的余角.所以cos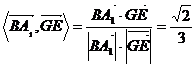 , 所以
, 所以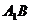 与平面
与平面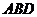 所成角为
所成角为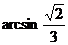 .
.
 (2)由(1)知
(2)由(1)知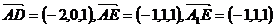 ,设平面
,设平面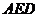 的法向量为
的法向量为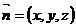 ,
,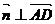 ,即
,即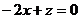 ,
,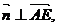 即
即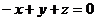 ,所以令法向量
,所以令法向量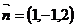 .所以点
.所以点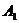 到平面
到平面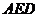 的距离为
的距离为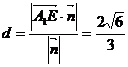 .
.
例4.过正方形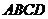 的顶点A,引
的顶点A,引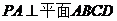 ,若
,若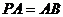 ,
,
则平面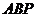 与平面
与平面
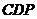 所成的二面角的大小.
所成的二面角的大小.
解:以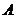 为原点,
为原点,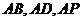 分别为
分别为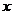 轴
轴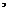
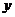 轴,
轴,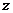 轴建立空间直角坐标系如图。
轴建立空间直角坐标系如图。
则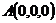 ,
,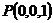 ,
, 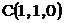 ,
, 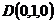 ,则
,则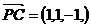 ,
,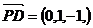 .设平面PCD的法向量为
.设平面PCD的法向量为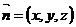 ,
,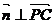 ,即
,即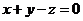 ;
;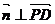 ,即
,即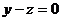 .所以可令
.所以可令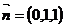 ;设平面PAB的法向量为
;设平面PAB的法向量为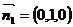 ,所以平面PAB与平面PCD所成的二面角的余弦值为
,所以平面PAB与平面PCD所成的二面角的余弦值为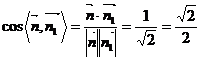 .所以平面
.所以平面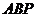 与平面
与平面
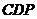 所成的二面角的平面角为
所成的二面角的平面角为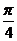 .
.
既然可以利用两个平面的法向量求两平面的夹角,也可以利用两个平面法向量证明两平面垂直.如下面的例5.可以先求两平面的法向量,再计算它们的数量积.
 例5.如图,正四棱柱
例5.如图,正四棱柱 中,底面边长为
中,底面边长为 ,侧棱长为4,
,侧棱长为4,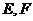 分别为棱
分别为棱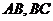 的中点.
的中点.
求证:平面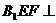 平面
平面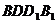
 解:以
解:以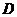 为原点,
为原点,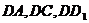 分别
分别
为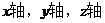 建立空间直角坐标系,则
建立空间直角坐标系,则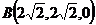 ,
,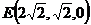 ,
,
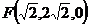
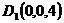
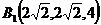
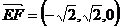
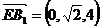
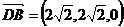 ,
,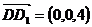 ,
,
设平面EF的法向量为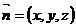 ,
,
则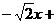
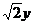 =0;
=0;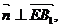 即
即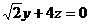 .所以令
.所以令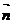 =
=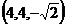
设平面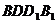 的法向量为
的法向量为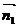 =
=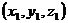 ,
,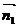
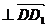 ,即4
,即4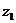 =0;
=0; 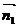
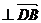 ,即
,即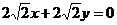 .所以可令
.所以可令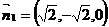 .
.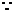
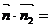
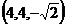
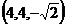 =0
=0
 平面
平面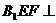 平面
平面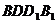 .
.