
1.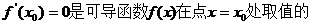 ( )
( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2.已知集合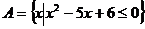 ,
,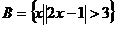 ,则集合
,则集合 (
)
(
)
A.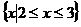 B.
B.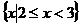
C.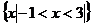 D.
D.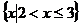
3.某校高一高二年级各有300人,高三年级有400人,现采用分层抽样抽取容量为50人的
样本,那么高三年级应抽人数为 ( )
A.16 B.40 C.20 D.25
4.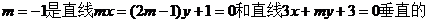 ( )
( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
5.地球半径为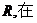 北纬30。的圆上,
北纬30。的圆上,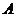 点经度为东经120。,
点经度为东经120。,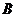 点的经度为西经60。
点的经度为西经60。
则 两点的球面距离为
( )
两点的球面距离为
( )
A.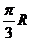 B.
B.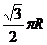 C.
C.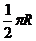 D.
D.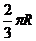
6.若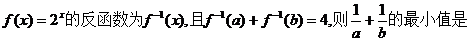
( )
A.1 B. C.
C.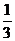 D.
D.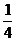
7.直线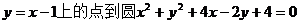 上的点的最近距离是 ( )
上的点的最近距离是 ( )
A.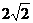 B.
B. 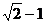 C.
C.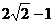 D.1
D.1
8.把编号为1.2.3.4.5的5位运动员排在编号为1.2.3.4.5的5条跑道中,要求
有上只有两位运动员的编号与其所在跑道的编号相同,共有不同的排法种数 ( )
A.10 B.20 C.40 D.60
9.已知函数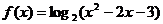 ,则使
,则使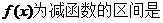 ( )
( )
A.(3,6) B.(-1,0) C.(1,2) D.(-3,-1)
10.函数
再把图象上各点的横坐标扩大到原来的2倍(纵坐标不变)则所得到的图象的解析式为
|
A.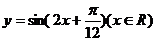 B.
B.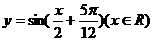
C.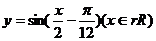 D.
D.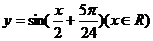
11.已知向量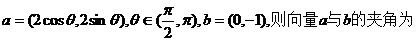
( )
A.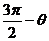 B.
B.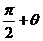 C.
C.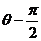 D.
D.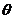
12.我们把离心率为黄金比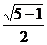 的椭圆称为“优美椭圆”(也叫黄金椭圆),已知
的椭圆称为“优美椭圆”(也叫黄金椭圆),已知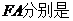 “优美椭圆”的左焦点和右顶点,B是它的短轴的一个端点,则
“优美椭圆”的左焦点和右顶点,B是它的短轴的一个端点,则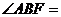
( )
A.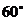 B.
B.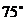 C.
C.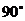 D.
D.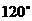
B卷
13.
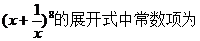
14. 已知
已知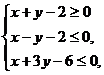 则
则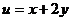 的最大值是
的最大值是
15. 等比数列
等比数列 的前
的前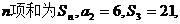 则公比
则公比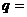
16.关于正四棱锥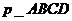 ,给出下列命题:
,给出下列命题:
①异面直线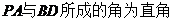
②侧面为锐角三角形;
③侧面与底面所成的二面角大于侧棱与底面所成的角;
④相邻两侧面所成的二面角为钝角。
 其中正确命题的序号是
其中正确命题的序号是
17.(本小题满分10分)
已知函数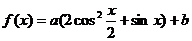 。
。
(Ⅰ)当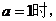 求
求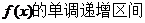
(Ⅱ)当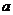 >0,且
>0,且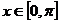 时,
时,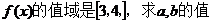 。
。
18.(本小题满分12分) 篮球总决赛采取五局三胜制,即有一队胜三场比赛就结束,预计本次决赛的两队实力相当,且每场比赛门票收入100万元,问:
篮球总决赛采取五局三胜制,即有一队胜三场比赛就结束,预计本次决赛的两队实力相当,且每场比赛门票收入100万元,问:
(Ⅰ)在本次比赛中,门票总收入是300万元的概率是多少?
(Ⅱ)在本次比赛中,门票总收入不低于400万元的概率是多少?
19.(本小题满分12分)如图,正棱柱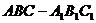 中,
中,
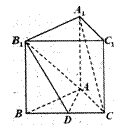 (Ⅰ)求证:
(Ⅰ)求证: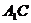 ∥平面
∥平面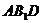 ;
;
(Ⅱ)求点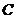 到平面
到平面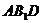 的距离。
的距离。
21.(本小题满分12分)设数列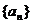 的前n项和为
的前n项和为 ,数列
,数列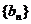 为等比数列,
为等比数列,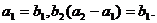
(1)求数列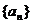 和
和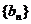 的通项公式;
的通项公式;
(2)设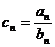 ,数列
,数列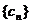 的前n项为Tn,求Tn(n
的前n项为Tn,求Tn(n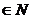 )
)
21.(本小题满分12分)p为椭圆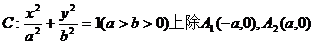 的两点外的一点。
的两点外的一点。
(Ⅰ)求直线
(Ⅱ)设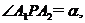 求证:
求证: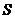 △
△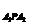 =-
=-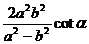 。
。
22.(本小题满分12分)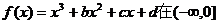 上为增函数在[0,2]上减函数,又方程
上为增函数在[0,2]上减函数,又方程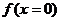 有三个根为
有三个根为 。
。
(Ⅰ)求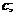
(Ⅱ)比较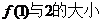 ;
;
(Ⅲ)求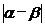 的范围。
的范围。
吉林省08届高考数学第五次模拟考试 试卷(文科) A卷参考答案
参考答案
BDCAD BCBDB AC
|
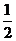 16.①②③④
16.①②③④ 
17.(10分)解:(1)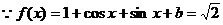
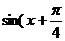
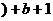 ,……3分
,……3分
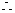 递增区间为[
递增区间为[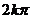 -
-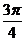 ,
,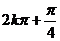 ](
](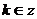 ) ………………5分
) ………………5分
2)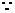
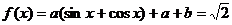
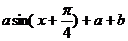 ,……………8分
,……………8分
而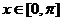 ,则
,则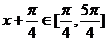 ,
, 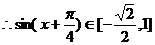
故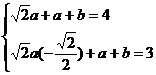
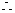
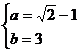 ………………10分
………………10分
18.解:①本次比赛,门票总收入是300万元,则前3场由某个队连胜,……… 2分
其概率为p1=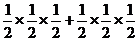 ………………………………………………。4分.
………………………………………………。4分.
=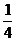 …………………………5分
…………………………5分
②本次比赛,门票总收入不低于心不忍400万元,则至少打4场,……………7分  概率为p2=2
概率为p2=2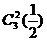 2(
2(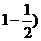
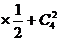 (
(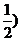 2(1-
2(1-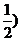 2
2
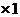 ………………………………10分
………………………………10分
=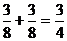 ……………………………………………………………11分
……………………………………………………………11分
答:略。 …………………………………………………………………12分
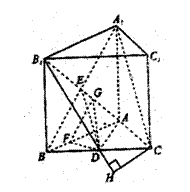 19. [解]解法一 (Ⅰ) 证明:
19. [解]解法一 (Ⅰ) 证明:
连接A1B, 设A1B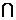 AB1=E. 连接DE
AB1=E. 连接DE
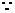 ABC-A1B1C1是正三棱柱,且AA1= AB,
ABC-A1B1C1是正三棱柱,且AA1= AB,
 四边形A1ABB1是正方形,
四边形A1ABB1是正方形,
 E是A1B的中点,又D是BC的中点,
E是A1B的中点,又D是BC的中点,
 DE//A1C。。。。。。。。。。。。。。。。。。。。。。。。。。3分
DE//A1C。。。。。。。。。。。。。。。。。。。。。。。。。。3分
 DE
DE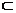 平面AB1D, A1C
平面AB1D, A1C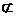 平面AB1D,
平面AB1D,
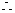 A1C//平面AB1D……………………5分
A1C//平面AB1D……………………5分
(Ⅱ) 解: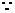 平面B1BCC1
平面B1BCC1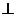 平面ABC,且A D
平面ABC,且A D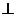 BC,
BC, 
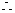 AD
AD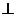 平面B1BCC1,又AD
平面B1BCC1,又AD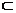 平面AB1D
平面AB1D
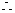 平面B1BCC1
平面B1BCC1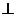 平面AB1D………………8分
平面AB1D………………8分
在平面B1BCC1内作CH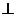 B1D交B1D的延长线于点H,
B1D交B1D的延长线于点H,
则CH的长度就是点C到平面AB1D的距离 ………………10分
由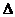 CDH∽
CDH∽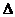 B1DB,得
B1DB,得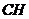 =
=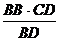 =
=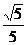 。
。
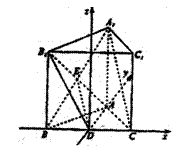 即点C到平面AB1D的距离是
即点C到平面AB1D的距离是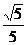 …………12分
…………12分
解法二:
建立空间直角坐标系D-xyz, 如图,
(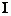 )证明:
)证明:
连接A1B,设A1B1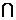 AB1=E,连接DE。
AB1=E,连接DE。
设AA1,=AB=1,
则D(0,0,0),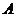 1 (0,
1 (0,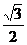 ,1),
,1), (-
(-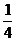 ,
,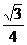 ,
, ),C(
),C( ,0,0)。
,0,0)。
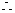
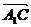 =(
=( ,
,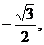 -1),
-1),
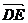
 =(-
=(-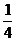 ,
,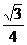 ,
, ),
),
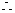
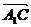 =-2
=-2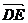 ,
,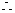
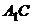 ∥
∥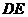 ……………………………………………3分
……………………………………………3分
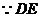
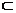 平面
平面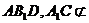 平面
平面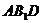
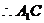 ∥平面
∥平面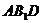 , ……………………………………………………………5分
, ……………………………………………………………5分
(Ⅱ)解: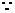
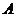 (0,
(0,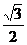 ,0),
,0),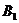 (-
(- ,0,1),
,0,1),
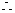
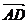 =(0,
=(0,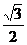 ,0),
,0),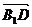 =(
=( ,0,-1)
,0,-1)
设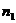 =(
=( )是平面AB1D的法向量。则,
)是平面AB1D的法向量。则,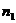 .
.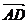 =0,且
=0,且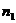 .
.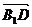 =0,……8分
=0,……8分
故-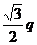 =0,
=0,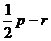 =0。取
=0。取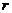 =1,得
=1,得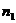 =(2,0,1)………………………10分
=(2,0,1)………………………10分
取其单位法向量 =(
=(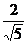 ,0,
,0,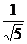 ),又
),又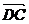 =(
=( ,O,O)
,O,O)
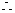 点C到平面AB1D的距离
点C到平面AB1D的距离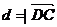 .
. |=
|=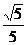 ……………………………………12分
……………………………………12分
20. 解:(1)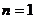 时,
时,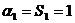
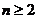 时,
时,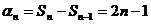 ,且该式当
,且该式当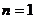 时也成立。
时也成立。
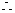
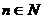 时,
时,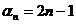 又
又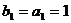 ,
,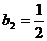 ,
,
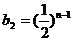 。。。。4分
。。。。4分
(2)解。 .2n-1
.2n-1
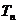 =1×1+3×
=1×1+3× +5×(
+5×( )2+7×(
)2+7×( )3+..+(2n-3)×(
)3+..+(2n-3)×( )n-2+(2n-1)×(
)n-2+(2n-1)×( )n-1
)n-1
(1)
 Tn=1×
Tn=1× +3×(
+3×( )2+5×(
)2+5×( )3+.. ... ... ...+(2n-3)×(
)3+.. ... ... ...+(2n-3)×( ) n-1+(2n-1)×(
) n-1+(2n-1)×( )n (2)
)n (2)
(1)-(2)得: Tn=1×1+2[
Tn=1×1+2[ +(
+( )2+(
)2+( )3+...+(
)3+...+( )n-1]-(2n-1)×(
)n-1]-(2n-1)×( )n
)n
=1×1+2×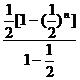 -(2n-1)(
-(2n-1)(
 )n
)n
Tn=3+(2n-3).2n …………………………12分
21. 解:设上点P(x,y)则有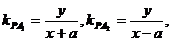 ……………………………………………………2分
……………………………………………………2分
由 变形为
变形为 …………………4分
…………………4分
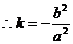 。即
。即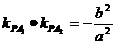 。 ………………………………………5分
。 ………………………………………5分
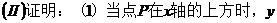
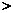 0。
0。
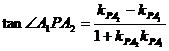 ,
,
 =
=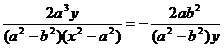 <0…………………7分
<0…………………7分
(2)当点P在x轴的下方时,y<0,同理可得 <0。
<0。
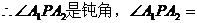
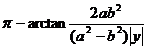 ……………………………9分
……………………………9分
由三角形的面积公式得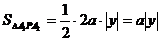
又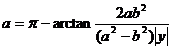
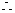
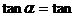 [
[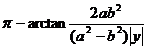 ]。
………………………………………10分
]。
………………………………………10分
得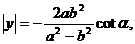
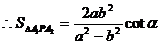 。
……………………………………………………12分
。
……………………………………………………12分
22.(12分) 解:(1)
解:(1)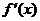 =
=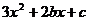
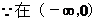 为增函数,(0,2)为减函数
为增函数,(0,2)为减函数
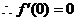
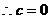 ………………………………………………3分
………………………………………………3分
(2)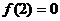
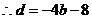
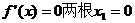
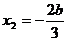
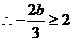

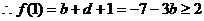 ……………………………………………………7分
……………………………………………………7分
(3)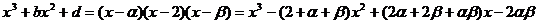 ……………………………………………………………9分
……………………………………………………………9分

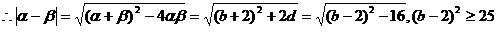
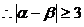 ………………………………………………………………………12分
………………………………………………………………………12分