
1.函数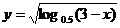 的定义域是
的定义域是
A.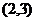 B.
B. 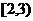 C.
C.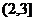 D.
D.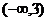
2.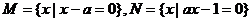 ,若M
,若M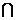 N=N,则实数
N=N,则实数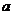 的值为
的值为
A.1 B.-1 C.1或-1 D.0或1或-1
3.设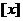 表示不超过
表示不超过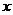 的最大整数,则
的最大整数,则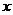 的不等式
的不等式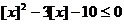 的解集是
的解集是
A.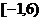 B.
B.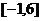 C.
C.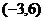 D.
D.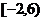
|
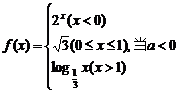 时,则
时,则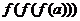 的值为
的值为
A.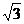 B.
B.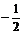 C.-2 D.2
C.-2 D.2
5.“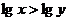 ”是“
”是“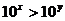 ”的
”的
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
6.函数 的反函数是
的反函数是
A.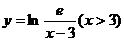 B.
B.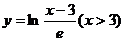
C. D.
D.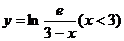
7.(理科)函数f(x)=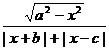 (0<a<b<c)的图象关于( )对称
(0<a<b<c)的图象关于( )对称
A.x轴 B.y轴 C.原点 D.直线y=x
(文科)函数f(x)=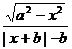 (0<a<b)的图象关于( )对称
(0<a<b)的图象关于( )对称
A.x轴 B.原点 C. y轴 D.直线y=x
|
|
|
|
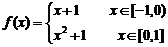 ,则下列函数的图象错误的是
,则下列函数的图象错误的是
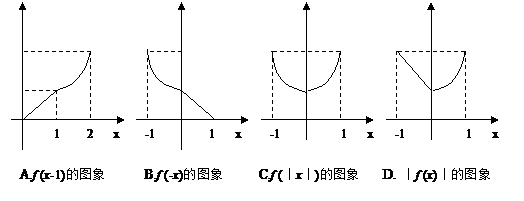
9.函数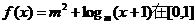 上的最大值和最小值之和为
上的最大值和最小值之和为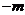 ,则
,则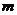 的值可以为
的值可以为
A.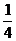 B.2 C.
B.2 C.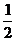 D.4
D.4
10.函数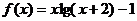 的图象与
的图象与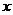 轴的交点个数为
轴的交点个数为
A.0个 B.1个 C.2个 D.3个
11.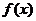 是定义在 R 上的以3为周期的奇函数,且
是定义在 R 上的以3为周期的奇函数,且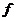 (2)=0,方程
(2)=0,方程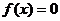 在区间(0,6)内解的个数的最小值是
在区间(0,6)内解的个数的最小值是
A.4 B.5 C.6 D.7
12.(理科)正实数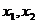 及函数
及函数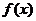 满足
满足 则
则
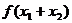 的最小值为
的最小值为
A.4 B.2 C.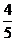 D.
D.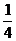
(文科)函数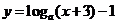
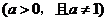 的图象恒过定点
的图象恒过定点 ,若点
,若点 在直线
在直线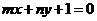 上,其中
上,其中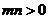 ,则
,则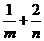 的最小值为
.
的最小值为
.
A.2 B.4 C.8 D.16
第Ⅱ卷 (非选择题 共90分)
13. 已知函数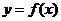 存在反函数
存在反函数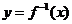 ,若函数
,若函数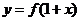 的图象经过点
的图象经过点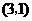 ,则函数
,则函数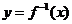 的图象必经过点 .
的图象必经过点 .
14. 已知集合P={(x,y)|y=m},Q={(x,y)|y=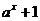 ,a>0,a≠1},如果P
,a>0,a≠1},如果P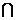 Q有且只有一个元素,那么实数m的取值范围是________.
Q有且只有一个元素,那么实数m的取值范围是________.
15.(理科)已知函数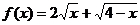 ,则函数
,则函数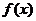 的值域为
.
的值域为
.
(文科)已知函数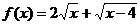 ,则函数
,则函数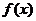 的值域为
.
的值域为
.
16.对于函数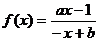 ,(
,(
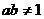 )有下列命题:
)有下列命题:
①函数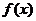 的定义域是
的定义域是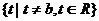 ,值域是
,值域是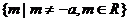 ;
;
②函数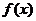 的图像是中心对称图形,且对称中心是
的图像是中心对称图形,且对称中心是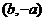 ;
;
③函数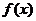 在
在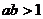 时,在
时,在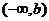 与
与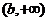 上单调递增;
上单调递增;
④函数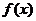 必有反函数
必有反函数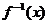 ,且当
,且当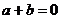 时,
时,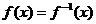 ;
;
⑤不等式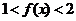 的解集就是不等式
的解集就是不等式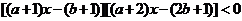 的解集.
的解集.
其中正确的命题有 .
17.( 本小题满分12分)设全集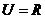 ,集合
,集合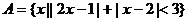 ,
,
B={ ,
求
,
求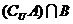
18.(本小题满分12分)已知函数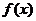 =
=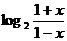
(1) 求证: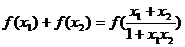 ;
;
(2)若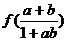 =1,
=1,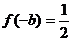 ,求
,求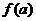 的值
的值
19. (本小题满分12分)设函数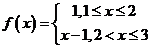 ,
,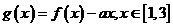 ,
,
其中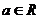 ,记函数
,记函数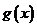 的最大值与最小值的差为
的最大值与最小值的差为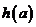 。
。
(I)求函数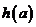 的解析式;
的解析式;
(II)画出函数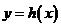 的图象并指出
的图象并指出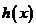 的最小值。
的最小值。
20.(本小题满分12分)
偶函数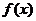 在
在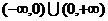 有定义,且在
有定义,且在 上是减函数,
上是减函数,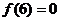 ,设
,设
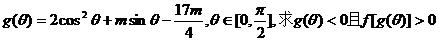 时
时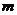 的取值范围。
的取值范围。
21. (理科)(本小题满分12分)设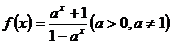
(1)求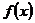 的反函数
的反函数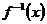 ;
;
(2)讨论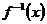 在
在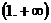 上的单调性,并加以证明;
上的单调性,并加以证明;
(3)令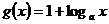 ,当
,当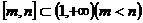 时,
时,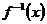 在
在 上的值域是
上的值域是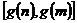 ,求
,求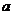 的取值范围。
的取值范围。
(文科)已知函数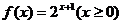 ,将函数
,将函数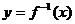 的图象沿着向量
的图象沿着向量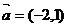 平移得到函数
平移得到函数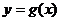 的图象。
的图象。
(1) 求函数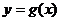 的解析式及定义域;
的解析式及定义域;
(2) 求出 的最小值及取得最小值时的
的最小值及取得最小值时的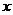 的值.
的值.
22. (本小题满分14分)已知函数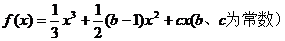 .
.
(1)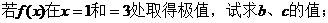
(2)若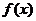 在
在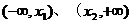 上单调递增,且在
上单调递增,且在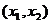 上单调递减,又满足
上单调递减,又满足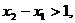 求证:
求证: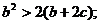
(3)在(2)的条件下,若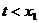 ,试比较
,试比较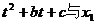 的大小,并加以证明。
的大小,并加以证明。
08届高考数学第一次模拟考试试卷 数学 考试时间:120分钟 满分:150分 第Ⅰ卷 (选择题 共60分)参考答案
答 案
一、选择题(本大题共12小题,每题5分,满分60分)
1.B 2.D 3.D 4.B 5.A 6.A 7.B 8.D 9.C 10.C 11.D 12.C
二、填空题(本大题4共小题,每题4分,满分16分)
13.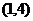 14.
14.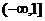 15.(理)[2,2
15.(理)[2,2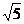 ] (文)[4,
] (文)[4,
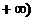 16.①②③④⑤
16.①②③④⑤
三、解答题:本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤。
17.解:当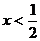 时,原不等式变形为
时,原不等式变形为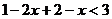 ,解得
,解得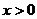

当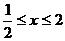 时,原不等式变形为
时,原不等式变形为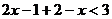 ,解得
,解得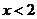
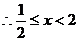
当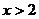 时,原不等式变形为
时,原不等式变形为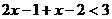 ,解得
,解得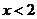
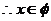
综上,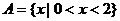 6分
6分
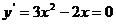 ,解得
,解得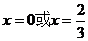
当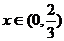 时,
时,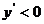 ;
;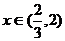 时,
时,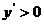
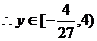 即
即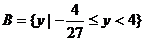
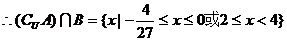 . 12分
. 12分
18.(1)证明: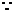
 =log
=log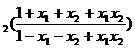
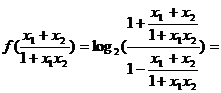 log
log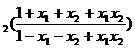

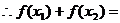
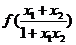 。 6分
。 6分
(2)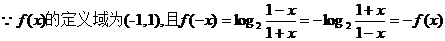
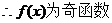 。
。
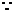
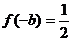 ,
,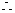
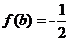 由(1)得
由(1)得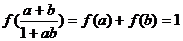
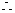
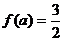 12分
12分
19.解:(I)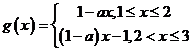
(1)当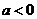 时,函数
时,函数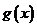 是
是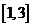 增函数,
增函数,
此时,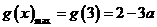 ,
,
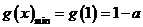 ,所以
,所以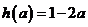 ;--2分
;--2分
(2)当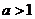 时,函数
时,函数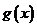 是
是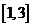 减函数,此时,
减函数,此时,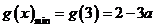 ,
,
 ,所以
,所以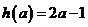 ;----4分
;----4分
(3)当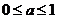 时,若
时,若 ,则
,则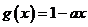 ,有
,有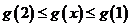 ;
;
若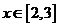 ,则
,则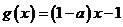 ,有
,有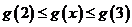 ;
;
因此,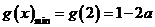 ,----6分
,----6分
而 ,
,
故当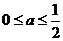 时,
时,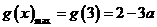 ,有
,有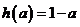 ;
;
 当
当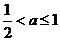 时,
时, ,有
,有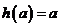 ;----8分
;----8分
综上所述: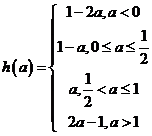 。----9分
。----9分
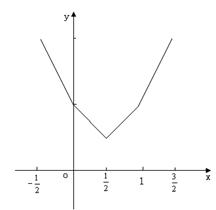
(II)画出 的图象,如右图。----11分
的图象,如右图。----11分
数形结合,可得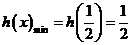 。----12分
。----12分
20.解:由题设知,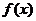 在
在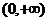 是增函数,且
是增函数,且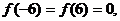 故在
故在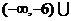
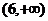 上
上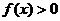 ,
,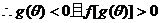 等价于
等价于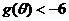 . 3分
. 3分
即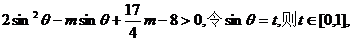
设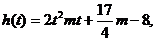 原问题等价于:函数
原问题等价于:函数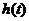 在区间
在区间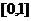 最小值大于0。 5分
最小值大于0。 5分
(i)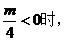 函数
函数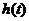 在区间
在区间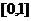 最小值为
最小值为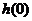
 矛盾 7分
矛盾 7分
(ii)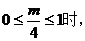 函数
函数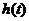 在区间
在区间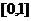 最小值为
最小值为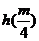 ,
,
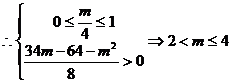 .
9分
.
9分
(iii)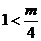 时,函数
时,函数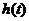 在区间
在区间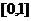 最小值为
最小值为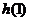 ,
,
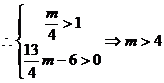 11分
11分
综上: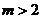 12分
12分
21.(理)解:(1)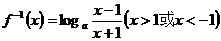 3分
3分
(2)设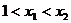 ,∵
,∵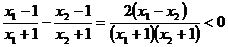
∴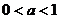 时,
时,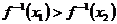 ,∴
,∴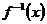 在
在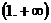 上是减函数:
上是减函数:
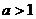 时,
时,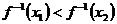 ,∴
,∴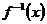 在
在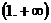 上是增函数。7分
上是增函数。7分
(3)当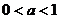 时,∵
时,∵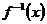 在
在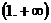 上是减函数
上是减函数
∴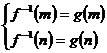 ,由
,由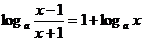 得
得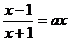 ,
,
即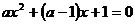 ,
,
可知方程的两个根均大于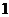 ,即
,即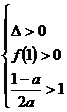
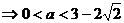 10分
10分
当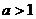 时,∵
时,∵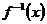 在
在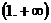 上是增函数
上是增函数
∴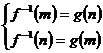
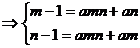
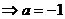 (舍去)。
(舍去)。
综上,得 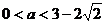 。
12分
。
12分
(文)解:(1)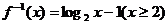 2分
2分
设 为函数
为函数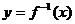 图象上任意一点,
图象上任意一点,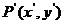 为平移后的对应点,则
为平移后的对应点,则
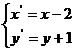 解得
解得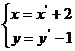 且
且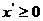 4分
4分
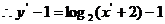
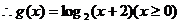 6分
6分
(2)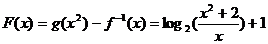
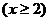 8分
8分
设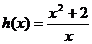 =
= ,令
,令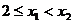 ,
,
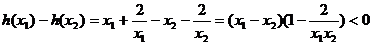
 10分
10分
当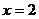 时,
时,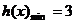 ,故当
,故当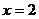 时,
时,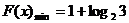 12分
12分
22.解:(1)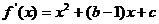
根据题意,1和3是方程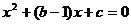 的两根,
的两根,
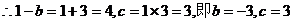 .
4分
.
4分
(2)由题意知,当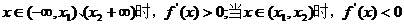 ,
,
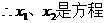
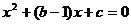 的两根,
的两根,
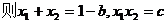
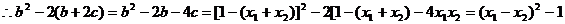
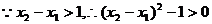 ,
, 即
即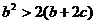 . 8分
. 8分
(3)在(2)的条件下,由上题知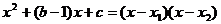
即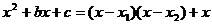
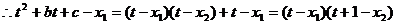
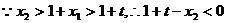 ,又
,又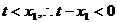
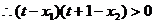 ,故
,故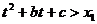 14分
14分