
1.(0712广东深圳)设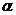 、
、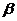 是两个平面,
是两个平面,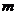 、
、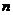 是两条不同的直线,则下列命题正确的是( ) A.若
是两条不同的直线,则下列命题正确的是( ) A.若 ,且
,且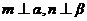 ,则
,则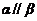
B.若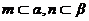 ,且
,且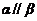 ,则
,则
C.若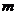 、
、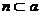 ,且
,且 ,则
,则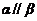
D.若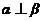 ,
,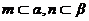 ,则
,则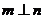
2.(0711山东临沂)设集合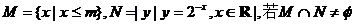 ,则实数m的取值范围是 ( )
,则实数m的取值范围是 ( )
A.m≥0 B.m>0 C.m≤0 D.m<0
3. (理科)(0712山东临沂)节假日时,国人发手机短信问候亲友已成为一种时尚,若小李的40名同事中,给其发短信问候的概率为1,0.8,0.5,0的人数分别是8,15,14,3(人),通常情况下,小李应收到同事问候的信息条数为 ( )
A.27 B.37 C.38 D.8
3.(0709山东临沂)下列说法错误的是 ( )
A.在统计里,把所需考察对象的全体叫作总体
B.一组数据的平均数一定大于这组数据中的每个数据
 C.平均数、众数与中位数从不同的角度描述了一组数据的集中趋势
C.平均数、众数与中位数从不同的角度描述了一组数据的集中趋势
D.一组数据的方差越大,说明这组数据的波动越大
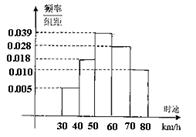
4.(0712山东青岛)200辆汽车经过某一雷达地区,时速频率分布直方图如图所示,则时速超过60km/h的汽车数量为 ( )
A.65辆 B.76辆
C.88辆 D.95辆
5.(0711山东临沂)现有一组实验数据如下表:则最佳的体现这些数据关系的函数模型是
|
t |
1.99 |
3.0 |
4.0 |
5.1 |
6.12 |
|
u |
1.5 |
4.04 |
7.5 |
1.2 |
18.01 |
A.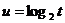 B.
B.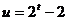 C.
C.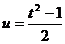 D.
D.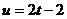
6. (0712山东临沂)某一供电网络有n个用电单位,若每个单位在一天中用电的概率是p,那么供电网络中一天平均用电的单位个数是 ( )
A.np(1-p) B.np C.n D.p(1-p)
7.(理科)(0712山东临沂)若(1+5x)n的展开式中各项系数之和为an,(7x2+5)n的展开式中各项的二项式系数之和为bn,则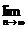
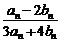 的值是
(
)
的值是
(
)
A.1 B.-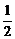 C.
C.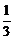 D.
D.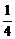
7.(0712山东临沂)给定集合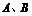 ,定义
,定义
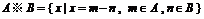 .若
.若 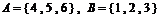 ,则集合
,则集合 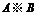 中的所有元素之和为 ( )
中的所有元素之和为 ( )
A. 15 B. 14 C. 27 D. -14
8、(0710山东宁津)甲用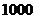 元买入一种股票,后将其转卖给乙,获利
元买入一种股票,后将其转卖给乙,获利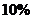 ,而后乙又将这些股票卖给甲,乙损失了
,而后乙又将这些股票卖给甲,乙损失了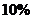 ,最后甲按乙卖给甲的价格九折将股票售出,甲在上述交易中
(
)
,最后甲按乙卖给甲的价格九折将股票售出,甲在上述交易中
(
)
A、盈亏平衡
B、盈利 元 C、盈利
元 C、盈利 元 D、亏本
元 D、亏本 元
元
9.(0712山东临沂)已知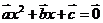 是关于
是关于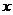 的一元二次方程,其中
的一元二次方程,其中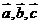 是非零向量,且
是非零向量,且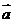 与
与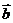 不共线,则方程
不共线,则方程
A. 可能有无数个实数解 B. 至多有两个实数解
C. 至少有一个实数解 D. 至多有一个实数解
10.(0709山东临沂)下列说法的正确的是 ( )
A.经过定点 的直线都可以用方程
的直线都可以用方程 表示
表示
B.经过定点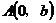 的直线都可以用方程
的直线都可以用方程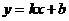 表示
表示
C.不经过原点的直线都可以用方程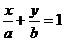 表示
表示
D.经过任意两个不同的点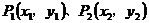 的直线都可以用方程
的直线都可以用方程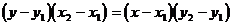 表示
表示
11.(0703山东淄博)如果以原点为圆心的圆经过双曲线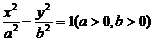 的顶点,并且被直线
的顶点,并且被直线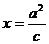 (c为双曲线的半焦距)分为弧长为3:1的两段弧,则该双曲线的离心等于( )
(c为双曲线的半焦距)分为弧长为3:1的两段弧,则该双曲线的离心等于( )
A.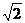 B.
B.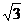 C.2 D.
C.2 D.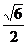
12.(0712山东青岛)对于集合M、N,定义M-N={x|x∈M,且x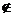 N},M
N},M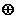 N=(M-N)∪(N-M),设A={t|t=x2-3x,x∈R},B={x|y=lg(-x)},则A
N=(M-N)∪(N-M),设A={t|t=x2-3x,x∈R},B={x|y=lg(-x)},则A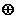 B=( )
B=( )
A.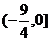 B.
B.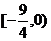
C.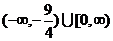 D.
D.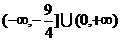
13. (0711山东烟台)关于x的实系数方程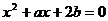 的一根在(0,1)内,另一根在(1,2)内,则点(a,b)所在区域的面积为 .
的一根在(0,1)内,另一根在(1,2)内,则点(a,b)所在区域的面积为 .
14. (0709山东临沂)有3张奖券,其中2张可中奖,现3个人按顺序依次从中抽一张,小明最后抽,则他抽到中奖券的概率是 .
15. (0711山东临沂)已知函数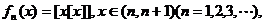 其中[x]表示不超过x的最大整数,如[-2.1]=-3,[-3]=-3,[2,5]=2,函数
其中[x]表示不超过x的最大整数,如[-2.1]=-3,[-3]=-3,[2,5]=2,函数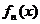 的值域中元素个数记为an,数列
的值域中元素个数记为an,数列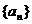 的前n项和为Sn,则满足
的前n项和为Sn,则满足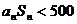 的最大正整数n等于
.
的最大正整数n等于
.
16.(0710山东宁津)对于函数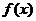 =
=  给出下列四个命题:
给出下列四个命题:
①该函数是以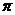 为最小正周期的周期函数;
为最小正周期的周期函数;
②当且仅当x =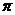 + k
+ k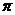 (k∈Z)时,该函数取得最小值是-1;
(k∈Z)时,该函数取得最小值是-1;
③该函数的图象关于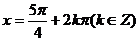 对称;
对称;
④当且仅当 时,
时,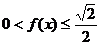 .
.
其中正确命题的序号是 .(请将所有正确命题的序号都填上)
17. (0709山东临沂)甲、乙两艘轮船都要在某个泊位停靠6小时,假定它们在一昼夜的时段中随机地到达,试求这两艘轮船中至少有一艘在停靠泊位时必须等待的概率.
18.(0712山东青岛)已知函数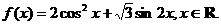
(I)求函数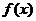 的最大值及此时x的值。
的最大值及此时x的值。
(II)若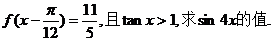
19. (0712山东青岛)在三棱锥M-ABC中,CM⊥平面ABC,MA=MB,NA=NB=NC.
(Ⅰ)求证:AM⊥BC;
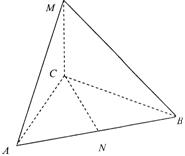 (Ⅱ)若∠AMB=60°,求直线AM与CN所成的角.
(Ⅱ)若∠AMB=60°,求直线AM与CN所成的角.
20.(0712山东临沂)若函数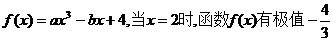 ,
,
(1)求函数的解析式;(2)若关于x的方程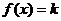 有三个零点,求实数k的取值范围.
有三个零点,求实数k的取值范围.
21. (0710山东宁津) 已知定义域为R的二次函数f(x)的最小值为0,且有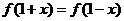 ,直线
,直线
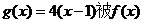 图象截得的弦长为
图象截得的弦长为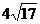 ,数列
,数列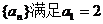 ,
,
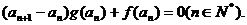
⑴ 求函数f(x)的解析式;
⑵ 求数列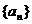 的通项公式;
的通项公式;
⑶ 设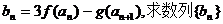 的最值及相应的n.
的最值及相应的n.
22.(理科)(0712山东临沂)已知函数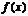 满足
满足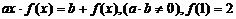 且
且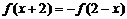 对定义域中任意
对定义域中任意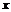 都成立.(1)求函数
都成立.(1)求函数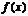 的解析式;
的解析式;
(2)若数列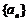 的前
的前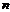 项和为
项和为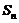 ,
,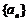 满足当
满足当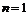 时,
时,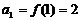 ,当
,当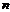 ≥2时,
≥2时,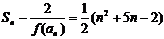 ,试给出数列
,试给出数列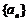 的通项公式,并用数学归纳法证明.
的通项公式,并用数学归纳法证明.
22. (0712山东青岛)已知椭圆9x2+2y2=18上任意一点P,由P向x轴作垂线段PQ,垂足为Q,点M在线段PQ上,且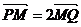 ,点M的轨迹为曲线E.
,点M的轨迹为曲线E.
(Ⅰ)求曲线E的方程;
(Ⅱ)若过定点F(0,2)的直线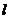 交曲线E于不同的两点G,H(点G在点F,H之间),且满足
交曲线E于不同的两点G,H(点G在点F,H之间),且满足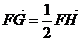 ,求直线
,求直线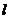 的方程.
的方程.
08届高考数学试题精选(三) 卞志业 2008-1-17参考答案
08届高考数学试题精选(三)答案
一、选择题:本大题主要考查基本知识和基本运算 共12小题,每小题5分,满分60分.
|
题 号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
答 案 |
A |
B |
A B |
B |
C |
B |
C A |
B |
D |
D |
|
C |
二、填空题: 本大题主要考查基本知识和基本运算. 本大题共4小题,每小题4分,满分16分。
13. 0.5 14. 2/3 _
15. 9 16. 3、4
三、解答题: 本大题共6小题,其中17~21题每题12分,22题14分,满分74分.解答应写出文字说明、演算步骤或推证过程.
17.解:甲到达时间为x,乙到达时间为y,则0<x , y<24. 4分
若至少有一艘在停靠泊位时必须等待,
则0<y-x<6或0<x-y<6 8分
必须等待的概率为:1-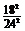 =
=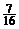 .
12分
.
12分
 8.解:(1)
8.解:(1)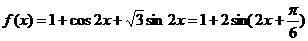 …………3分
…………3分
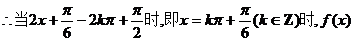 取最大值3 …………6分
取最大值3 …………6分
(II)由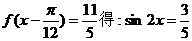 …………8分
…………8分
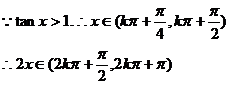
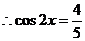 …………10分
…………10分
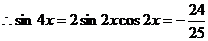 …………12分
…………12分
19.证明:(I)∵NA=NB=NC
∴N是△ABC外接圆的圆心,可得∠ACB=90°,即BC⊥AC……2分
∵CM⊥平面ABC,BC 平面ABC,
平面ABC,
∴MC⊥BC………………………………………………4分
∴BC⊥面MAC
∴BC⊥MA…………………………………………6分
(II)(文)取MB的中点P,连结CP,NP,则NP//AM,所以∠PNC是直线AM与CN所成的角,………………………………8分
令AN=NB=NC=1,
∴AM=2,NP=1,CP=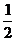 MB=1
MB=1
在△CPN中,CP=NP=CN=1………………10分
∴∠PNC=60°…………………………12分
20.解:由题意可知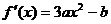 …………1分
…………1分
(1)于是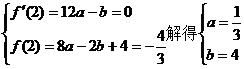 …………3分
…………3分
故所求的解析式为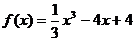 …………4分
…………4分
(2)由(1)可知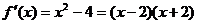
令 =0得x=2或x=-2 …………5分
=0得x=2或x=-2 …………5分
当x变化时 、
、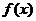 的变化情况如下表所示
的变化情况如下表所示
|
x |
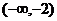 |
-2 |
(-2,2) |
2 |
(2,+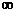 ) ) |
 |
+ |
0 |
- |
0 |
+ |
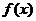 |
单调递增 |
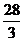 |
单调递减 |
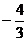 |
单调递增 |
|
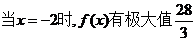
当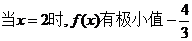 ……10分
……10分
所以函数的大致图象如图
故实数k的取值范围是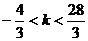 …………12分
…………12分
21. 解:(1)因为二次函数f(x)有最小值为0,所以a>0,又因为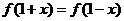 ,所以对称轴为x=1,所以设
,所以对称轴为x=1,所以设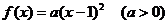 ……① 又
……① 又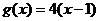 ……②
……②
联立①②组成方程组解得两图象的交点坐标为(1,0),(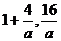 ),依题意得
),依题意得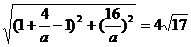 ,因为a>0,所以解得a=1,所以
,因为a>0,所以解得a=1,所以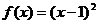 (4分)
(4分)
⑵由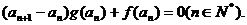 ,
,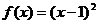 ,
,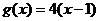
得,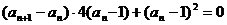 ,因为
,因为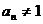 ,所以
,所以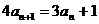 ,所以
,所以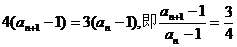 ,又
,又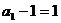 ,所以数列{
,所以数列{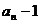 }是以1为首项,
}是以1为首项,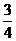 为公比的等比数列,所以
为公比的等比数列,所以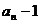 =1
=1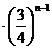 ,所以
,所以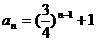 ……(9分)
……(9分)
(3)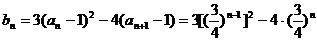
令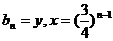
则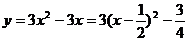 ………… (11分)
………… (11分)
因为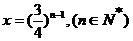
所以当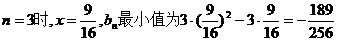 ……… (13分)
……… (13分)
当n = 1时,x=1,bn最大值为0 ………… (14分)
22.解:(1)由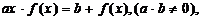 得
得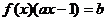 ,
,
若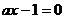 ,则
,则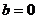 ,不合题意,故
,不合题意,故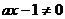 ,
, 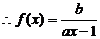 。
。
由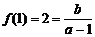 ,得
,得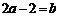 ……①
……①
由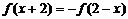 对定义域中任意
对定义域中任意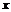 都成立,得
都成立,得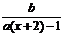
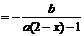 。
。
由此解得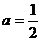 ……②
……②
把②代入①,可得
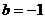 ,
, 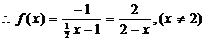
(2)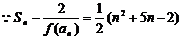 ,即
,即
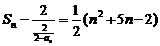 ,
,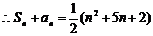
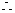 当
当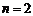 时,
时, ,
,
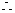 当
当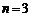 时,
时,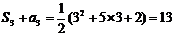 ,
,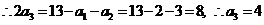
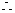 当
当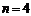 时,
时,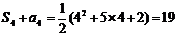 ,
,
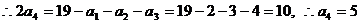 ,由此猜想:
,由此猜想: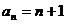 。
。
下面用数学归纳法证明:(1)当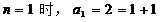 ,等式成立。
,等式成立。
(2)假设当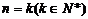 时,等式成立,就是
时,等式成立,就是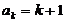
那么,当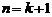 时,
时,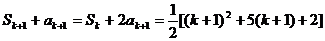 ,
,
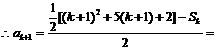
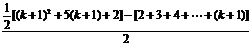
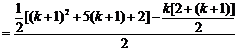
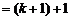
这就是说,当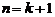 时,等式也成立。
时,等式也成立。
由(1)和(2)可知,等式对任何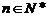 都成立,故猜想正确。
都成立,故猜想正确。
(2)解法二: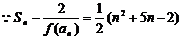 ,即
,即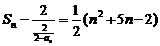
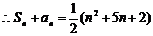 ,即
,即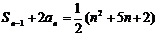
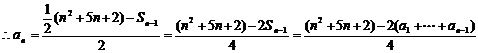
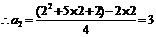 ,
,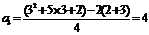 ,
,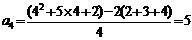
由此猜想: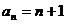 。
。
下面用数学归纳法证明:(1)当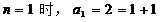 ,等式成立。
,等式成立。
(2)假设当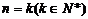 时,等式成立,就是
时,等式成立,就是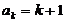
那么,当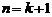 时,
时,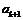
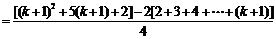
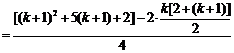
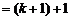
这就是说,当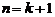 时,等式也成立。
时,等式也成立。
由(1)和(2)可知,等式对任何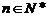 都成立,故猜想正确。
都成立,故猜想正确。
22.(文)解:(I)设点P(x0,y0),是椭圆上一点,则Q(x0,0),M(x,y)
由已知得:x0=x,y0=3y代入椭圆方程得
9x2+18y2=18即x2+2y2=2为曲线E的方程.……………………………………4分
(II)设G(x1,y1),H(x2,y2)
当直线GH斜率存在时,设直线GH的斜率为k
则直线GH的方程为:y=kx+2,……………………………………5分
代入x2+2y2=2,得:(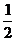 +k2)x2+4kx+3=0
+k2)x2+4kx+3=0
由△>0,解得:k2>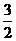 …………………………………………6分
…………………………………………6分
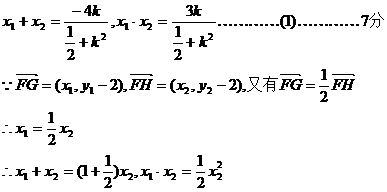
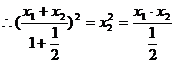 ……………………………………(2)
……………………………………(2)
∴将(1)代入(2)整理得: 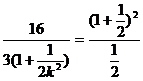 ………………9分
………………9分
解得: 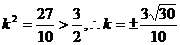 …………………………11分
…………………………11分
∴直线l的方程为:y=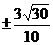 x+2…………………………12分
x+2…………………………12分
当直线GH斜率不存在时,直线的l方程为x=0,此时
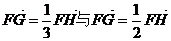 矛盾不合题意.
矛盾不合题意.
∴所求直线l的方程为:y=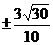 x+2…………………………14分
x+2…………………………14分