
1. 下列函数中,最小正周期为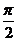 的是 (
)
的是 (
)
A.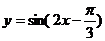 B.
B.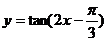
C.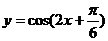 D.
D.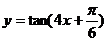
2. 已知等差数列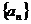 的公差为2, 若
的公差为2, 若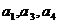 成等比数列, 则
成等比数列, 则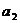 =(
)
=(
)
A . –4 B. –6 C. –8 D. –10
3. 已知函数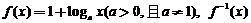 是
是 的反函数,若
的反函数,若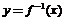 的图象过点(3,4),则
的图象过点(3,4),则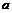 等于( )
等于( )
A.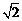 B.
B.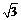 C.
C.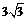 D.
D. 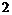
4.
若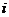 为虚数单位,则复数
为虚数单位,则复数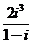 在复平面内对应的点在 (
)
在复平面内对应的点在 (
)
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.
(2x3-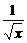 )7的展开式中常数项是(
)
)7的展开式中常数项是(
)
A 14 B
14 B -14
C
-14
C 42
D
42
D -42
-42
6. 设集合A={x|x2<a} ,B={x|x<2},若A∩B=A, 则实数a的取值范围是( )
A.a<4 B.a£4 C. 0<a£4 D. 0<a<4
7.
设抛物线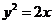 与过其焦点的直线交于
与过其焦点的直线交于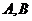 两点,则
两点,则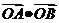 的值
的值
A
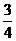 B
B
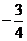 C
C
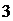 D
D
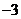
8.
已知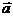 =(2,3),
=(2,3),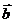 =(-4,7),则
=(-4,7),则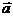 在
在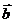 方向上的投影为(
)
方向上的投影为(
)
A
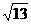
B
B
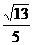 C
C
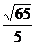
D
D
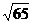
9. P为椭圆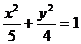 上的点,
上的点,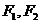 是两焦点,若
是两焦点,若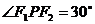 ,则
,则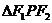 的面积是(
)
的面积是(
)
A.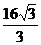 B.
B.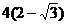 C.
C.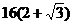 D. 16
D. 16
10. 在棱长为2的正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,E、F分别是CC1、AD的中点,那么异面直线OE和FD1所成的角的余弦值等于( )
A
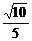 B
B
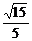 C
C
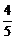 D
D
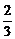
11.
若关于x的方程x2 - x + a = 0和x2 - x +
b = 0(a )的四个根可以组成首项为
)的四个根可以组成首项为 的等差数列,则a+b的值为( )
的等差数列,则a+b的值为( )
A.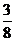 B.
B.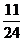 C.
C. 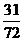 D.
D.
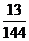
12.
定义行列式运算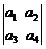 =
= .将函数
.将函数 的图象向左平移
的图象向左平移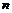 (
(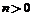 )个单位,所得图象对应的函数为偶函数,则
)个单位,所得图象对应的函数为偶函数,则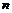 的最小值为( )
的最小值为( )
A.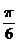 B.
B.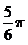 C.
C.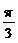 D.
D.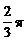
13. 函数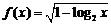 的定义域为 .
的定义域为 .
14. 过长方体的同一个顶点的三条棱长为3cm、4cm、5cm,且它的八个顶点都在一个球面上,这个球的表面积是 cm2.
15. 若椭圆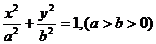 的离心率为
的离心率为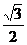 ,则双曲线
,则双曲线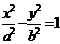 的离心率为_______
的离心率为_______
16.
定义“符号函数”f(x)=sgnx=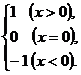
则不等式x+2>(x-2)sgnx的解集是___________.
武山三中2008届高三第四次模拟考试
08届高考理科数学第四次模拟考试试卷 本卷满分150分,答卷时间120分钟.答卷一律在答题纸上进行,只交答题纸.参考答案
数学理科参考答案
一、选择题(本大题共12个小题,每小题5分,共60分. )
1.B 2. B 3. D 4. D / C 5. A 6.B 7. B 8. C 9. B 10. B 11. C 12. B
二、填空题(本大题共4个小题,每小题5分,共20分. )
13. 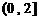 14. 50π 15.
14. 50π 15. 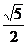 16. (-
16. (-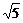 ,+∞)
,+∞)
三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤。)
17.解: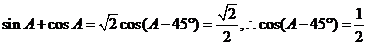
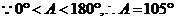 ,
,
所以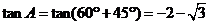 ,
,
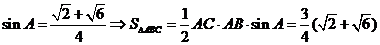 。
。
18.解:解: (1)由已知得A(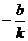 ,0), B(0,b),
,0), B(0,b),
则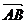 =(
=(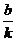 ,b),于是
,b),于是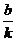 =2,b=2. ∴
=2,b=2. ∴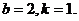 .
.
(2)由f(x)> g(x),得x+2>x2-x-6,即(x+2)(x-4)<0, 得-2<x<4,
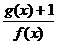 =
= =x+2+
=x+2+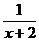 -5
-5
由于x+2>0,则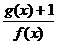 ≥-3,当且仅当x+2=1,即x=
-1时等号成立.
≥-3,当且仅当x+2=1,即x=
-1时等号成立.
∴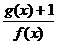 的最小值是-3.
的最小值是-3.
 19. 解:(1)证明:∵DE是△AOB的中位线
19. 解:(1)证明:∵DE是△AOB的中位线
∴DE∥OB
DE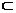 平面CDE
平面CDE
OB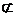 平面CDE
平面CDE
∴OB∥平面CDE
(2)解法一:
作OM⊥直线DE于M点,
∵CO⊥平面OAB,由三垂线定理CM⊥DE,作OH⊥CM于H
则OH⊥相交直线CM、ME,∴OH⊥平面CDE
已证OM,CM都垂直于DE,∴∠OMC是二面角O-DE-E的平面角 ,
cos∠OMC=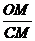 =
=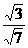 =
=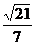 ,∴二面角O-DE-C的大小为arccos
,∴二面角O-DE-C的大小为arccos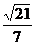
解法二:如图,以O为原点, 为z轴正向,
为z轴正向,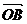 为y轴正向,在平面OAB内作OF⊥y轴并以
为y轴正向,在平面OAB内作OF⊥y轴并以 为x轴正向建立空间直角坐标系(如图)
为x轴正向建立空间直角坐标系(如图)
 则题意得:O(0,0,0),A(2
则题意得:O(0,0,0),A(2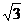 ,2,0)
,2,0)
 B(0,4,0),C(0,0,2)
B(0,4,0),C(0,0,2)
D(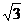 ,1,0),E(
,1,0),E(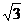 ,3,0)
,3,0)

 取平面CDE的法向量
取平面CDE的法向量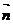 =(2,0,
=(2,0,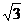 )
)
取平面OAB的法向量 =(0,0,2)
cos<
=(0,0,2)
cos<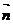 ,
, >=
>=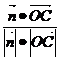 =
=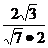 =
=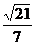
∴二面角O-DE-C的大小为arccos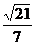
20. (1)解:设数列{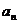 }公差为d,则
}公差为d,则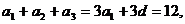
又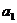 =2,d=2. 所以
=2,d=2. 所以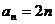 ;
;
(2)解:令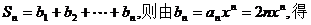
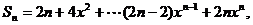 ①
①
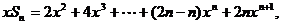 ②
②
当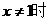 ①式减去②式,得
①式减去②式,得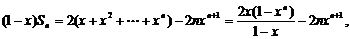
所以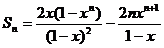
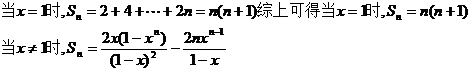 ①②
①②
21.解:(1)由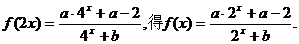
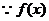 是R上的奇函数,
是R上的奇函数,
又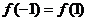
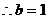
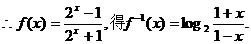
由此得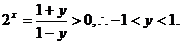 故反函数
故反函数 揎义域为(-1,1)
揎义域为(-1,1)
(2)当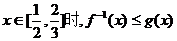 恒成立,
恒成立,
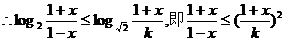
由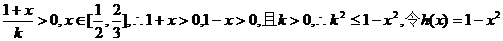
则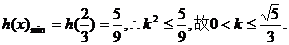
22.(Ⅰ)由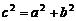 …①,
…①,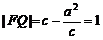 ,∴
,∴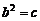 …②.
…②.
由中点坐标公式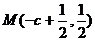 .
.
(Ⅱ)又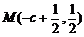 在双曲线上,∴
在双曲线上,∴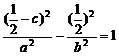 …③.
…③.
联立①②③,解得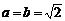 ,
,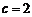 .
.
∴双曲线方程为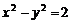 .
.
注:对点M用第二定义,得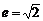 ,可简化计算.
,可简化计算.
(Ⅲ)由(Ⅱ), ,设
,设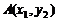 ,
,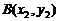 ,m:
,m: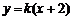 ,
,
则由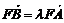 ,得
,得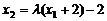 ,
, .
.
由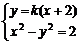 ,得
,得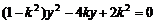 .
.
∴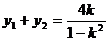 ,
,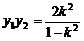 .
.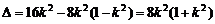 .
.
由 ,
,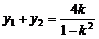 ,
,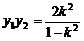 ,消去
,消去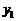 ,
,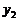 ,
,
得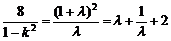 .
.
∵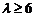 ,函数
,函数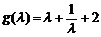 在
在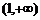 上单调递增,
上单调递增,
∴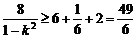 ,∴
,∴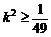 .
.
又直线m与双曲线的两支相交,即方程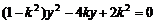 两根同号,
两根同号,
∴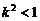 . ∴
. ∴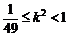 ,故
,故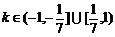 .
.