
1.已知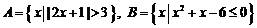 ,则
,则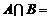 ( )
( )
A.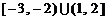 B.
B.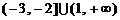
C.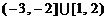 D.
D.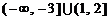
2.下列正方体或正四面体中,P、Q、R、S分别是所在棱的中点,这四个点不共面的一个图是 ( )


A B C D
3.直线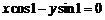 的倾斜角的大小是(
)
的倾斜角的大小是(
)
A.1 B. C.
C.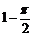 D.
D.
4.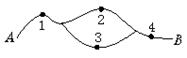 如图所示,在A、B间有四个焊接点,若焊接点脱落,则可能导致电路不通.今发现A、B之间线路不通,则焊接点脱落的不同情况有( )
如图所示,在A、B间有四个焊接点,若焊接点脱落,则可能导致电路不通.今发现A、B之间线路不通,则焊接点脱落的不同情况有( )
A.13种 B.12种 C.10种 D.14种
5.已知等差数列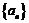 的前n项和为
的前n项和为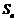 ,若
,若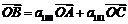 ,且
,且 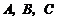 三点共线(该直线不过点O),则
三点共线(该直线不过点O),则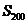 等于 ( )
等于 ( )
A.100 B.101 C.200 D.201
6.设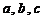 是互不相等的正数,则下列不等式中不恒成立的是( )
是互不相等的正数,则下列不等式中不恒成立的是( )
A.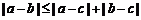 B.
B.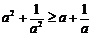
C.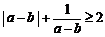 D.
D.
7. 连掷两次骰子分别得到点数m、n,向量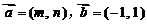 ,若
,若 中
中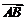 与
与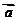 同向,
同向,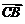 与
与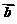 反向,则
反向,则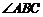 是钝角的概率是(
)
是钝角的概率是(
)
A.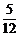 B.
B.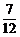 C.
C. D.
D.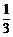
8.设x,y满足约束条件 ,则
,则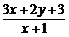 取值范围是( )
取值范围是( )
A.[ 1,5 ] B.[ 2,6 ] C.[ 1,10 ] D.[ 3,11 ]
9.在平面直角坐标系中,点P在直线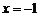 上运动,点Q满足
上运动,点Q满足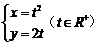 .若从动点P向Q点的轨迹引切线,则所引切线长的最小值为( )
.若从动点P向Q点的轨迹引切线,则所引切线长的最小值为( )
A.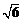 B.
B.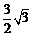 C.
C.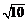 D.
D.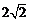
10.定义在R上的函数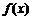 满足
满足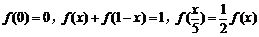 ,且当
,且当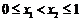 时,
时,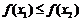 .则
.则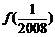 等于( )
等于( )
A.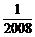 B.
B.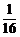 C.
C.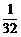 D.
D.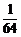
|
11.命题“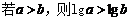 ”的否命题为
.
”的否命题为
.
12.二项式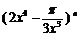
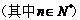 的展开式中含有非零常数项,则n的最小值为 .
的展开式中含有非零常数项,则n的最小值为 .
13. 曲线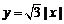 和
和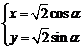 (
(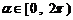 )所围成的较小区域的面积是
.
)所围成的较小区域的面积是
.
14.设椭圆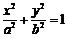 (a > b > 0)的右焦点为F1,右准线为l1,若过F1且垂直于x轴的弦的长等于点F1到l1的距离,则椭圆的离心率是
.
(a > b > 0)的右焦点为F1,右准线为l1,若过F1且垂直于x轴的弦的长等于点F1到l1的距离,则椭圆的离心率是
.
15.设函数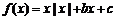 ,给出下列命题:①
,给出下列命题:①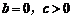 时,方程
时,方程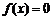 只有一个实数根;②
只有一个实数根;②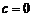 时,
时,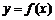 是奇函数;③方程
是奇函数;③方程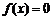 至多有两个实根.上述三个命题中所有正确命题的序号为 .
至多有两个实根.上述三个命题中所有正确命题的序号为 .
16.路灯距地面为8米,一个身高为1.7米的人以每秒1.4米的速度匀速地从路灯的正底下沿某直线离开路灯,那么人影的变化速率为 .
17.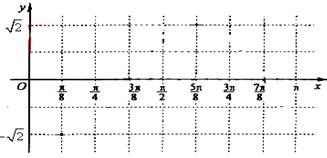 (本题满分13分)已知向量
(本题满分13分)已知向量 ,
, 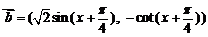 ,记
,记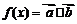 .
.
(1) 求函数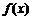 的最大值,最小正周期;
的最大值,最小正周期;
(2) 作出函数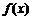 在区间[0,π]上的图象.
在区间[0,π]上的图象.
18.(本题满分13分)一次考试中共 12道选择题,每道题都有4个选项,其中有且只有一个选项是正确答案.每题答对得5分,不答或答错得0分.某考生已确定有8道题的答案是正确的,其余题中:有两道题可以判断两个选项是错误的,有一道题可以判断一个选项是错误的,还有一道因不理解题意只好乱猜.
(1) 分别计算出该考生得50分、60分的概率;
(2) 列出该考生所得分数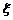 的分布列并求其数学期望.
的分布列并求其数学期望.
19.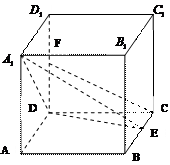 (本题满分13分)在边长为2的正方体
(本题满分13分)在边长为2的正方体 中,E是BC的中点,F是
中,E是BC的中点,F是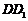 的中点.
的中点.
(1) 求证:CF∥平面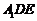 ;
;
(2) 求点A到平面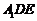 的距离;
的距离;
(3) 求二面角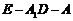 的平面角的大小(结果用反余弦表示).
的平面角的大小(结果用反余弦表示).
20. (本大题满分13分)设函数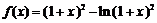 .
.
(1) 求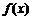 的单调区间;
的单调区间;
(2) 若关于x的方程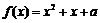 在区间
在区间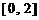 上恰有两个相异实根,求实数a的取值范围.
上恰有两个相异实根,求实数a的取值范围.
21.(本大题满分12分)已知椭圆C的焦点在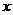 轴上,它的一个顶点恰好是抛物线
轴上,它的一个顶点恰好是抛物线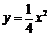 的焦点,离心率等于
的焦点,离心率等于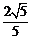 .
.
(1) 求椭圆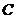 的方程;
的方程;
(2) 过椭圆C的右焦点F作直线l交椭圆C于A,B两点,交y轴于点M.若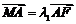 ,
,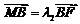 ,求证:
,求证: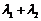 为定值.
为定值.
22. (本大题满分12分)在数列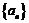 中,
中,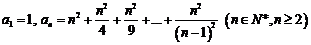 .
.
证明:(1) 当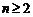 时,
时,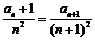 ;
;
(2) 当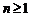 时,
时,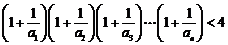 .
.
08届高考理科数学第六次月考试题 数学试题(理科)2008年3月 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟. 第Ⅰ卷 (选择题 共50分)参考答案
08届高考理科数学第六次月考试题参考答案
一、选择题 ADDAA CADBC
|
11.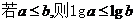 ; 12.7; 13.
; 12.7; 13.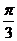 ; 14.
; 14.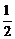 ; 15.①②; 16.
; 15.①②; 16.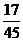 .
.
三、解答题:
17. ⑴
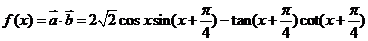
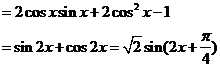 ……………6分
……………6分
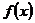 的最大值为
的最大值为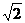 , 最小正周期
, 最小正周期 ……………8分
……………8分
⑵略。……………12分
18. 解:(1)设”可判断两个选项是错误的”两道题之一选对的为事件A,”有一道题可以判断一个选项是错误”选对的为事件为B,“有一道不理解题意”选对的为事件C,
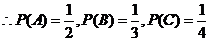 , ………..(3分)
, ………..(3分)
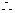 得50分的概率为
得50分的概率为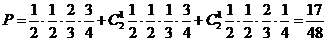 ; ……..(5分 )
; ……..(5分 )
得60分的概率为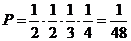 .
……(7分)
.
……(7分)
(2)得40分概率为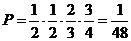 ;
;
得45分的概率为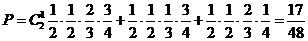 ;
;
得55分的概率为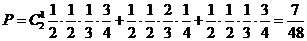 .
……….(11分)
.
……….(11分)
所以 …………(13分)
…………(13分)
19.解: (1)取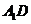 中点
中点 连接
连接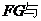
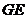 ,则易证四边形
,则易证四边形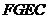 是矩形.所以
是矩形.所以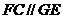 ,又
,又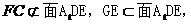 所以
所以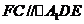 . ………….(4分)
. ………….(4分)
(2)易算得, ,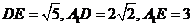 ,
,
所以由余弦定理得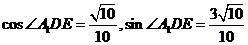 ,则
,则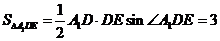 又
又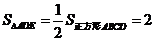 , …………(6分)
, …………(6分)
用等积法: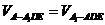 ,得点A到平面
,得点A到平面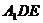 的距离为
的距离为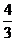 . ………….(8分)
. ………….(8分)
(3)取边 的中点P,连接PE,易知
的中点P,连接PE,易知 ,则
,则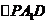 是
是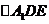 在上的射影。
…………..(10分)
在上的射影。
…………..(10分)
计算得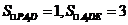 ,所以二面角
,所以二面角 的平面角
的平面角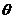 的余弦值为
的余弦值为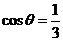 ,
……………(12分)
,
……………(12分)
 .
……………(13分)
.
……………(13分)
20. 解:⑴定义域为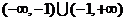 ,
,
因为 ……………..…(2分 )
……………..…(2分 )
所以,当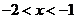 或
或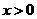 时,
时,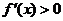
当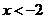 或
或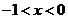 时,
时,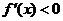 …………………(4分)
…………………(4分)
故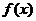 的单调递增区间是
的单调递增区间是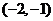 和
和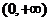 ……………………
(5分)
……………………
(5分)
⑵由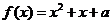 得:
得: ,
,
令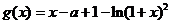 ,
……………………(7分)
,
……………………(7分)
则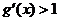 或
或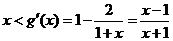
所以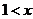 ≤
≤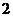 时,
时,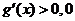 ≤
≤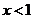 时,
时,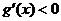
故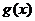 在
在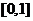 上递减,在
上递减,在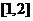 上递增
…………………..(9分)
上递增
…………………..(9分)
要使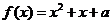 在
在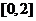 恰有两相异实根,则必须且只需
恰有两相异实根,则必须且只需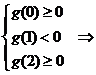
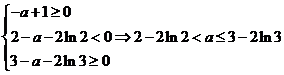
则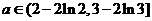 ……………..(12分)
……………..(12分)
21.(1).设椭圆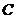 的方程为
的方程为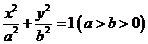 ,则由题意得
,则由题意得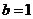 . ……..(2分)
. ……..(2分)
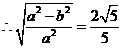 ,即
,即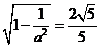 ,所以
,所以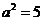 .
………………….(4分)
.
………………….(4分)
故椭圆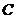 的方程为
的方程为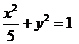 .
………………………….(5分)
.
………………………….(5分)
(2).设点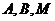 的坐标分别为
的坐标分别为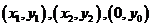 .
.
易知点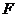 的坐标为
的坐标为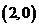 .
.
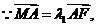
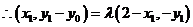 ,则
,则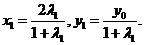
将点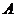 的坐标代入到椭圆方程中,得
的坐标代入到椭圆方程中,得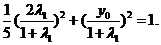
化简得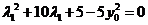 .
…………………………….…..(8分)
.
…………………………….…..(8分)
同理,由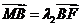 得
得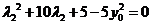 ,
,
所以,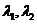 是方程
是方程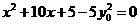 的两个根,
…………….…..(11分)
的两个根,
…………….…..(11分)
 …………….…..(12分)
…………….…..(12分)
22.(1).当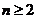 时,
时,

所以, 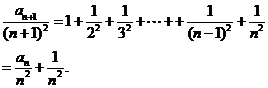 ……………………(3分)
……………………(3分)
故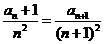 .
………………………(5分)
.
………………………(5分)
(2).当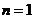 时,
时,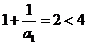 ,结论成立;
……………………..(6分)
,结论成立;
……………………..(6分)
当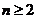 时,
时,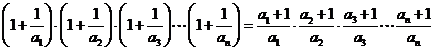
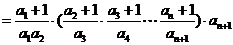 ……………………..(8分)
……………………..(8分)
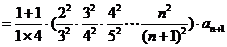
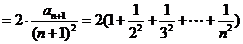
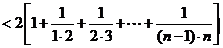 …………………….(10分)
…………………….(10分)
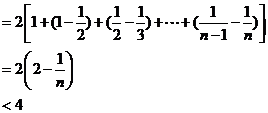
综上述,对任意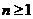 ,不等式成立.
………………………….(12分)
,不等式成立.
………………………….(12分)