
4.(人教A版105习题3.3A组第2题)
画出不等式组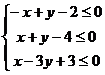 表示的平面区域.
表示的平面区域.
变式1:点(-2,t)在直线2x-3y+6=0的上方,则t的取值范围是______
解:(-2,t)在2x-3y+6=0的上方,则2×(-2)-3t+6<0,解得t>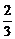
 答案:t>
答案:t>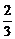
设计意图:熟悉判断不等式所代表的区域的方法.
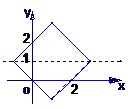
变式2:求不等式|x-1|+|y-1|≤2表示的平面区域的面积
解:|x-1|+|y-1|≤2可化为
 或
或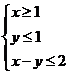 或
或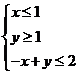 或
或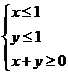
其平面区域如图
∴面积S=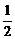 ×4×4=8
×4×4=8
设计意图:不同形式的可行域的作图.
5.(人教A版113页习题3.4A组第1题)
(1)把36写成两个正数的积,当这两个正数取什么值时,它们的和最小?
(2)把18写成两个正数的和,当这两个正数取什么值时,它们的积最大?
变式1:函数y =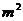 +
+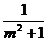 的值域为
的值域为

解:y=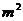 +
+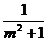 = (
= (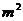 +1)+
+1)+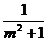 -1≥2-1=1 ,所以值域为[1, +∞)
-1≥2-1=1 ,所以值域为[1, +∞)
设计意图:均值不等式的灵活应用.
变式2:设x≥0, y≥0, x2+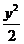 =1,则
=1,则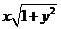 的最大值为__
的最大值为__
解法一: ∵x≥0, y≥0, x2+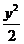 =1
=1
∴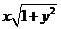 =
=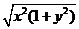 =
=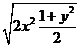
≤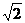
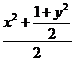 =
=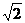
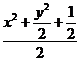 =
=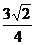
当且仅当x=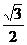 ,y=
,y=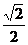 (即x2=
(即x2= 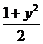 )时,
)时, 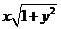 取得最大值
取得最大值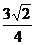
解法二:
令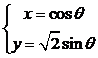 (0≤
(0≤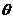 ≤
≤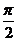 )
)
则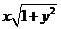 =cos
=cos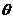
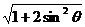 =
=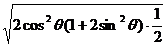
≤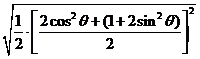 =
=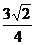
当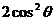 =
=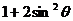 ,
,
即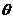 =
=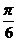 时,x=
时,x=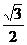 ,y=
,y=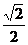 时,
时,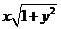 取得最大值
取得最大值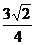

设计意图:均值不等式的灵活应用.
6.(人教A版115复习参考题A组第2题)
已知集合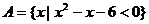 ,
,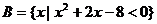 ,求
,求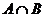 .
.
变式1:已知A={x|x3+3x2+2x>0},B={x|x2+ax+b≤0}且A∩B={x|0<x≤2},A∪B={x|x>-2},求a、b的值
解:A={x|-2<x<-1或x>0},
设B=[x1,x2],由A∩B=(0,2]知x2=2,
且-1≤x1≤0, ①
由A∪B=(-2,+∞)知-2≤x1≤-1 ②
②
由①②知x1=-1,x2=2,
∴a=-(x1+x2)=-1,b=x1x2=-2
设计意图:一元二次不等式与集合的运算综合。
变式2:解关于x的不等式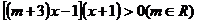

解:下面对参数m进行分类讨论:
①当m=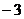 时,原不等式为x+1>0,∴不等式的解为
时,原不等式为x+1>0,∴不等式的解为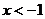

②当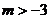 时,原不等式可化为
时,原不等式可化为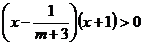

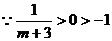 ,∴不等式的解为
,∴不等式的解为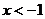 或
或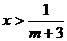

③当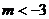 时,原不等式可化为
时,原不等式可化为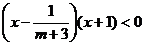

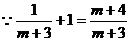 ,
,
当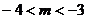 时,
时,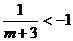 原不等式的解集为
原不等式的解集为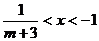 ;
;
当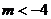 时,
时,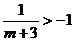 原不等式的解集为
原不等式的解集为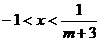 ;
;
当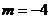 时,
时,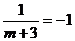 原不等式无解
原不等式无解
综上述,原不等式的解集情况为:
①当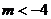 时,解为
时,解为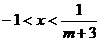 ;
;
②当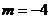 时,无解;
时,无解;
③当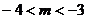 时,解为
时,解为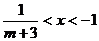 ;
;
④当m=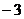 时,解为
时,解为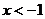 ;
;
⑤当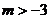 时,解为
时,解为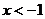 或
或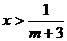

设计意图:含参数的一元二次不等式的解法。
7. (人教A版115复习参考题B组第1题)
求证: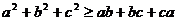
变式1:己知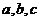 都是正数,且
都是正数,且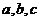 成等比数列,
成等比数列,
求证: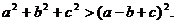
证明: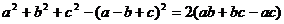
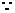
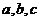 成等比数列,
成等比数列,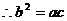

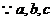 都是正数,
都是正数,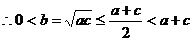

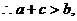
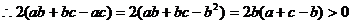

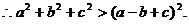
设计意图:基本不等式的灵活应用。
变式2:若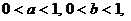 ,求证ab与
,求证ab与 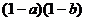 不能都大于
不能都大于

证明:假设ab, (1-a) (1-b)都大于 
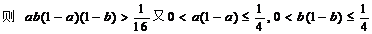
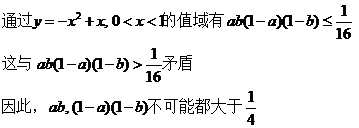
设计意图:基本不等式与累乘、反证法综合应用。
8. (人教A版116复习参考题B组第7题)
要制造一个无盖的盒子,形状为长方体,底宽为2m。现有制盒材料60m2,当盒子的长、高各为多少时,盒子的体积最大?
变式1:今有一台坏天平,两臂长不等,其余均精确,有人说要用它称物体的重量,只需将物体放在左右托盘各称一次,则两次称量结果的和的一半就是物体的真实重量,这种说法对吗?并说明你的结论
解:不对
设左、右臂长分别是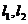 ,物体放在左、右托盘称得重量分别为
,物体放在左、右托盘称得重量分别为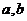 真实重量为为G,则由杠杆平衡原理有:
真实重量为为G,则由杠杆平衡原理有:
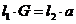 ,
,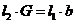
①×②得G2=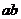 , ∴G=
, ∴G=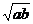
由于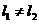 ,故
,故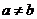 ,由平均值不等式
,由平均值不等式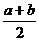 >
> 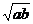 知说法不对
知说法不对
设计意图:基本不等式的应用。