
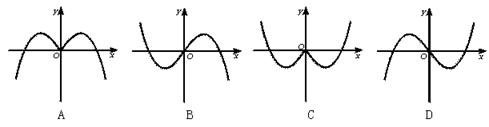
1.()函数y=-x.cosx的部分图象是( )
2.()函数f(x)=cos2x+sin(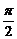 +x)是( )
+x)是( )
A.非奇非偶函数 B.仅有最小值的奇函数
C.仅有最大值的偶函数 D.既有最大值又有最小值的偶函数
3.()函数f(x)=(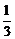 )|cosx|在[-π,π]上的单调减区间为_________.
)|cosx|在[-π,π]上的单调减区间为_________.
4.()设ω>0,若函数f(x)=2sinωx在[-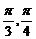 ,]上单调递增,则ω的取值范围是_________.
,]上单调递增,则ω的取值范围是_________.
5.()设二次函数f(x)=x2+bx+c(b,c∈R),已知不论α、β为何实数恒有f(sinα)≥0和f(2+cosβ)≤0.
(1)求证:b+c=-1;
(2)求证c≥3;
(3)若函数f(sinα)的最大值为8,求b,c的值.
6.()用一块长为a,宽为b(a>b)的矩形木板,在二面角为α的墙角处围出一个直三棱柱的谷仓,试问应怎样围才能使谷仓的容积最大?并求出谷仓容积的最大值.
7.()有一块半径为R,中心角为45°的扇形铁皮材料,为了获取面积最大的矩形铁皮,工人师傅常让矩形的一边在扇形的半径上,然后作其最大内接矩形,试问:工人师傅是怎样选择矩形的四点的?并求出最大面积值.
8.()设-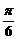 ≤x≤
≤x≤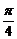 ,求函数y=log2(1+sinx)+log2(1-sinx)的最大值和最小值.
,求函数y=log2(1+sinx)+log2(1-sinx)的最大值和最小值.
9.()是否存在实数a,使得函数y=sin2x+a.cosx+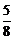 a-
a-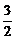 在闭区间[0,
在闭区间[0,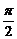 ]上的最大值是1?若存在,求出对应的a值;若不存在,试说明理由.
]上的最大值是1?若存在,求出对应的a值;若不存在,试说明理由.
难点15 三角函数的图象和性质 三角函数的图象和性质是高考的热点,在复习时要充分运用数形结合的思想,把图象和性质结合起来.本节主要帮助考生掌握图象和性质并会灵活运用. ●难点磁场 ()已知α、β为锐角,且x(α+β-)>0,试证不等式f(x)=x<2对一切非零实数都成立. ●案例探究 [例1]设z1=m+(2-m2)i,z2=cosθ+(λ+sinθ)i,其中m,λ,θ∈R,已知z1=2z2,求λ的取值范围. 命题意图:本题主要考查三角函数的性质,考查考生的综合分析问题的能力和等价转化思想的参考答案
参考答案
难点磁场
证明:若x>0,则α+β> ∵α、β为锐角,∴0<
∵α、β为锐角,∴0< -α<β<
-α<β< ;0<
;0< -β<
-β< ,∴0<sin(
,∴0<sin( -α)<sinβ.0<sin(
-α)<sinβ.0<sin( -β)<sinα,∴0<cosα<sinβ,0<cosβ<sinα,∴0<
-β)<sinα,∴0<cosα<sinβ,0<cosβ<sinα,∴0<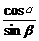 <1,0<
<1,0<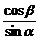 <1,∴f(x)在(0,+∞)上单调递减,∴f(x)<f(0)=2.若x<0,α+β<
<1,∴f(x)在(0,+∞)上单调递减,∴f(x)<f(0)=2.若x<0,α+β< ,∵α、β为锐角,0<β<
,∵α、β为锐角,0<β< -α<
-α< ,0<α<
,0<α< -β<
-β< ,0<sinβ<sin(
,0<sinβ<sin( -α),∴sinβ<cosα,0<sinα<sin(
-α),∴sinβ<cosα,0<sinα<sin( -β),∴sinα<cosβ,∴
-β),∴sinα<cosβ,∴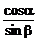 >1,
>1, 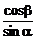 >1,
>1,
∵f(x)在(-∞,0)上单调递增,∴f(x)<f(0)=2,∴结论成立.
歼灭难点训练
一、1.解析:函数y=-xcosx是奇函数,图象不可能是A和C,又当x∈(0,  )时,
)时,
y<0.
答案:D
2.解析:f(x)=cos2x+sin( +x)=2cos2x-1+cosx
+x)=2cos2x-1+cosx
=2[(cosx+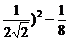 ]-1.
]-1.
答案:D
二、3.解:在[-π,π]上,y=|cosx|的单调递增区间是[- ,0]及[
,0]及[ ,π].而f(x)依|cosx|取值的递增而递减,故[-
,π].而f(x)依|cosx|取值的递增而递减,故[- ,0]及[
,0]及[ ,π]为f(x)的递减区间.
,π]为f(x)的递减区间.
4.解:由- ≤ωx≤
≤ωx≤ ,得f(x)的递增区间为[-
,得f(x)的递增区间为[- ,
, ],由题设得
],由题设得
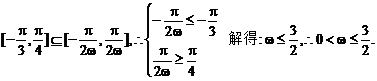
三、5.解:(1)∵-1≤sinα≤1且f(sinα)≥0恒成立,∴f(1)≥0
∵1≤2+cosβ≤3,且f(2+cosβ)≤0恒成立.∴f(1)≤0.
从而知f(1)=0∴b+c+1=0.
(2)由f(2+cosβ)≤0,知f(3)≤0,∴9+3b+c≤0.又因为b+c=-1,∴c≥3.
(3)∵f(sinα)=sin2α+(-1-c)sinα+c=(sinα-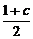 )2+c-(
)2+c-(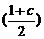 )2,
)2,
当sinα=-1时,[f(sinα)]max=8,由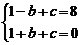 解得b=-4,c=3.
解得b=-4,c=3.
6.解:如图,设矩形木板的长边AB着地,并设OA=x,OB=y,则a2=x2+y2-2xycosα≥2xy-2xycosα=2xy(1-cosα).
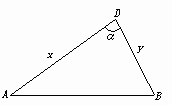
∵0<α<π,∴1-cosα>0,∴xy≤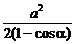 (当且仅当x=y时取“=”号),故此时谷仓的容积的最大值V1=(
(当且仅当x=y时取“=”号),故此时谷仓的容积的最大值V1=(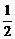 xysinα)b=
xysinα)b=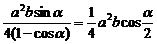 .同理,若木板短边着地时,谷仓的容积V的最大值V2=
.同理,若木板短边着地时,谷仓的容积V的最大值V2=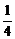 ab2cos
ab2cos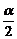 ,
,
∵a>b,∴V1>V2
从而当木板的长边着地,并且谷仓的底面是以a为底边的等腰三角形时,谷仓的容积最大,其最大值为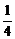 a2bcos
a2bcos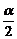 .
.
7.解:如下图,扇形AOB的内接矩形是MNPQ,连OP,则OP=R,设∠AOP=θ,则
∠QOP=45°-θ,NP=Rsinθ,在△PQO中,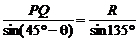 ,
,
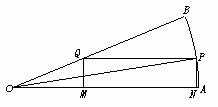
∴PQ=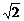 Rsin(45°-θ).S矩形MNPQ=QP.NP=
Rsin(45°-θ).S矩形MNPQ=QP.NP=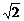 R2sinθsin(45°-θ)=
R2sinθsin(45°-θ)= R2.[cos(2θ-45°)-
R2.[cos(2θ-45°)- ]≤
]≤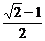 R2,当且仅当cos(2θ-45°)=1,即θ=22.5°时,S矩形MNPQ的值最大且最大值为
R2,当且仅当cos(2θ-45°)=1,即θ=22.5°时,S矩形MNPQ的值最大且最大值为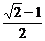 R2.
R2.
工人师傅是这样选点的,记扇形为AOB,以扇形一半径OA为一边,在扇形上作角AOP且使∠AOP=22.5°,P为边与扇形弧的交点,自P作PN⊥OA于N,PQ∥OA交OB于Q,并作OM⊥OA于M,则矩形MNPQ为面积最大的矩形,面积最大值为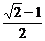 R2.
R2.
8.解:∵在[-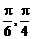 ]上,1+sinx>0和1-sinx>0恒成立,∴原函数可化为y=
]上,1+sinx>0和1-sinx>0恒成立,∴原函数可化为y=
log2(1-sin2x)=log2cos2x,又cosx>0在[-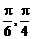 ]上恒成立,∴原函数即是y=2log2cosx,在x∈[
]上恒成立,∴原函数即是y=2log2cosx,在x∈[
-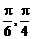 ]上,
]上, ≤cosx≤1.
≤cosx≤1.
∴log2 ≤log2cosx≤log21,即-1≤y≤0,也就是在x∈[-
≤log2cosx≤log21,即-1≤y≤0,也就是在x∈[-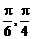 ]上,ymax=0,
]上,ymax=0,
ymin=-1.
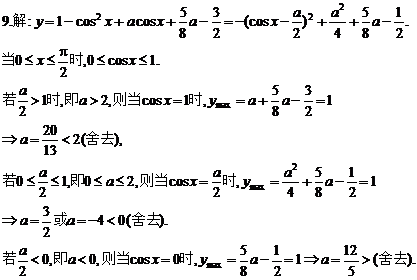
综合上述知,存在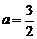 符合题设.
符合题设.