
1.设集合P={1,2,3,4},Q={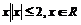 },则P∩Q等于( )
},则P∩Q等于( )
A.{1,2} B. {3,4}
C. {1} D. {-2,-1,0,1,2}
2.函数y=2cos2x+1(x∈R)的最小正周期为 ( )
A.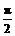 B.
B.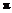 C.
C.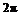 D.
D.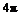
3.从4名男生和3名女生中选出4人参加某个座谈会,若这4人中必须既有男生又有女生,则不同的选法共有( )
A.140种 B.120种 C.35种 D.34种
4.一平面截一球得到直径是6cm的圆面,球心到这个平面的距离是4cm,则该球的体积是( )
A.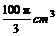 B.
B. 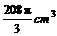 C.
C. 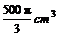 D.
D. 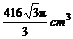
5.若双曲线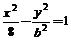 的一条准线与抛物线
的一条准线与抛物线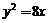 的准线重合,则双曲线的离心率为
( )
的准线重合,则双曲线的离心率为
( )
A.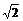 B.
B.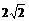 C.
4 D.
C.
4 D.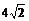
7.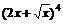 的展开式中x3的系数是( )
的展开式中x3的系数是( )
A.6 B.12
C.24 D.48
8.若函数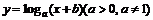 的图象过两
的图象过两
点(-1,0)和(0,1),则( )
A.a=2,b=2 B.a=,b=2
C.a=2,b=1 D.a=,b=
9.将一颗质地均匀的骰子(它是一种各面上分
别标有点数1,2,3,4,5,6的正方体玩具)先后抛掷3次,至少出现一次6点向上的概率是( )
A. B. C. D.
10.函数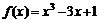 在闭区间[-3,0]上的最大值、最小值分别是( )
在闭区间[-3,0]上的最大值、最小值分别是( )
A.1,-1 B.1,-17 C.3,-17 D.9,-19
11.设k>1,f(x)=k(x-1)(x∈R) . 在平面直角坐标系xOy中,函数y=f(x)的图象与x轴交于A 点,它的反函数y=f -1(x)的图象与y轴交于B点,并且这两个函数的图象交于P点. 已知四边形OAPB的面积是3,则k等于 ( )
A.3 B. C. D.
12.设函数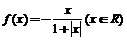 ,区间M=[a,b](a<b),集合N={
,区间M=[a,b](a<b),集合N={ },则使M=N成立的实数对(a,b)有 ( )
},则使M=N成立的实数对(a,b)有 ( )
A.0个 B.1个 C.2个 D.无数多个